
On the other hand, E[Ya]=aP(Ya a)=aP(X>a) From which we obtain aP(X≥a)≤E(X)
◼ On the other hand, 𝐄 𝑌𝑎 = 𝑎P 𝑌𝑎 = 𝑎 = 𝑎P X ≥ a ◼ From which we obtain 𝑎P 𝑋 ≥ 𝑎 ≤ 𝐄(𝑋)
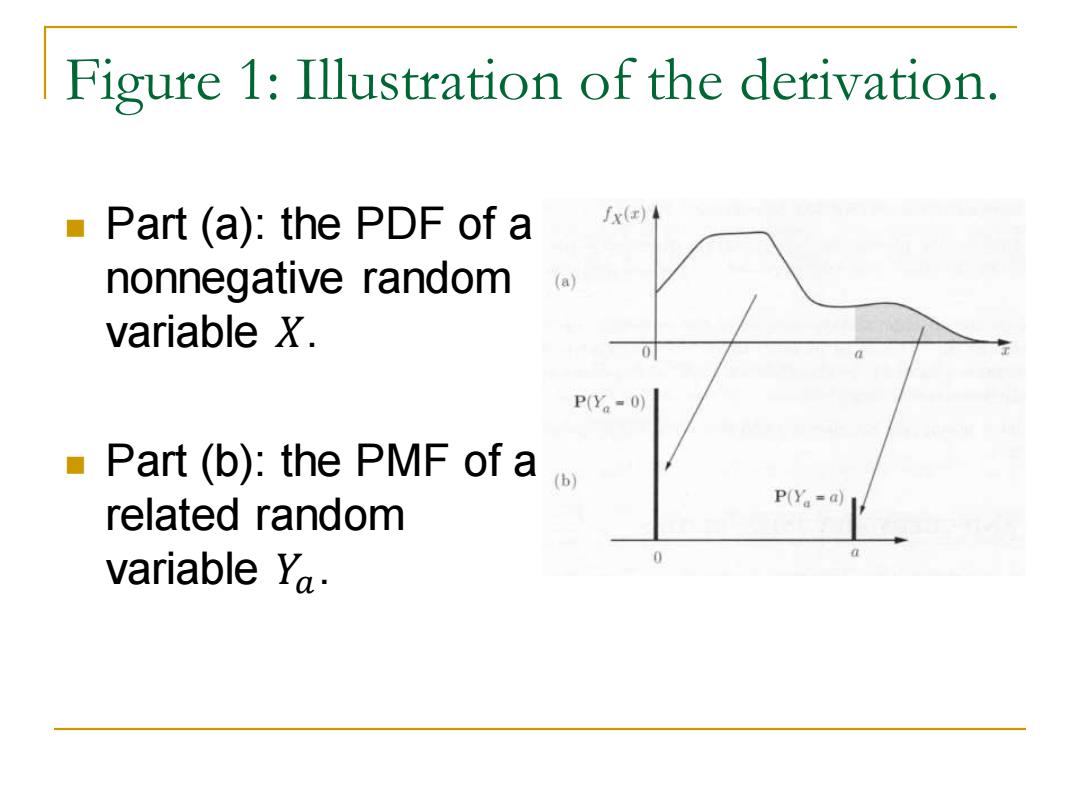
Figure 1:Illustration of the derivation. Part (a):the PDF of a fx() nonnegative random (a) variable X. 0 P(Ya-0) Part (b):the PMF of a related random P(Ya=a) variable Ya. 0
◼ Part (a): the PDF of a nonnegative random variable 𝑋. ◼ Part (b): the PMF of a related random variable 𝑌𝑎. Figure 1: Illustration of the derivation

Figure 1:Illustration of the derivation. All of the mass in the x() PDF of X that lies between 0 and a is (a) assigned to 0, ■ All of the mass that lies above a is to a. P(Y-0) Since mass is shifted to the left,the expectation (b P(Ya=a) can only decrease and therefore E[X]≥E[Ya] aP(Ya a) =aP(X≥a):
◼ All of the mass in the PDF of 𝑋 that lies between 0 and 𝑎 is assigned to 0, ◼ All of the mass that lies above 𝑎 is to 𝑎. ◼ Since mass is shifted to the left, the expectation can only decrease and therefore 𝐄 𝑋 ≥ 𝐄 𝑌𝑎 = 𝑎P 𝑌𝑎 = 𝑎 = 𝑎P 𝑋 ≥ 𝑎 . Figure 1: Illustration of the derivation

Example 1. Let X be uniformly distributed in 0,4]. Note that EX]=2. Then,the Markov inequality asserts that 2 P(X≥2)≤ P(X≥3)≤ 三 0.67. P(X≥4)≤ 4 三 0.5
Example 1. ◼ Let 𝑋 be uniformly distributed in 0,4 . ◼ Note that 𝐄[𝑋] = 2. ◼ Then, the Markov inequality asserts that P 𝑋 ≥ 2 ≤ 2 2 = 1. P 𝑋 ≥ 3 ≤ 2 3 = 0.67. P 𝑋 ≥ 4 ≤ 2 4 = 0.5

Example 1. By comparing with the exact probabilities 2 P(X≥2)≤ 21 P(X≥2)=0.5. P(X≥3)≤ 3 =0.67.P(X≥3)=0.25. P(X≥4)≤ 4 =0.5.P(X≥4)=0. We see that the bounds provided by the Markov inequality can be quite loose
Example 1. ◼ By comparing with the exact probabilities P 𝑋 ≥ 2 ≤ 2 2 = 1. P 𝑋 ≥ 2 = 0.5. P 𝑋 ≥ 3 ≤ 2 3 = 0.67. P 𝑋 ≥ 3 = 0.25. P 𝑋 ≥ 4 ≤ 2 4 = 0.5. P 𝑋 ≥ 4 = 0. ◼ We see that the bounds provided by the Markov inequality can be quite loose