
Tresca 屈服准则 (最大剪应力准则) Imax=K 01-03=2k (01≥02≥03) Mises 屈服准则 0。=0, 回忆: g-万a-+o,-a+o-o .=5Va,-0,+o,-0+a-0+6G++
Tresca 屈服准则(最大剪应力准则) Mises 屈服准则 回忆: ] m x a = K 1 3 1 2 3 − = 2 ( ) k e s = 2 2 2 1 2 2 3 3 1 1 ( ) ( ) ( ) 2 e = − + − + − 1 2 2 2 2 2 2 ( ) ( ) ( ) 6( ) 2 e x y y z z x xy yz zx = − + − + − + + +

比较两屈服准则的区别: (1)物理含义不同:Tresca:最大剪应力达到极限值K Mises:畸变能达到某极限 (2)表达式不同; (3)几何表达不同: Tresca准则:在主应力空间中为一垂直m平面的正六棱柱; Mises准则:在主应力空间中为一垂直于π平面的圆柱。 (π平面:在主应力坐标系中,过原点并垂直于等倾线的平面)
比较两屈服准则的区别: (1)物理含义不同:Tresca:最大剪应力达到极限值K Mises :畸变能达到某极限 (2)表达式不同; (3)几何表达不同: Tresca准则:在主应力空间中为一垂直π平面的正六棱柱; Mises 准则:在主应力空间中为一垂直于π平面的圆柱。 (π平面:在主应力坐标系中,过原点并垂直于等倾线的平面)
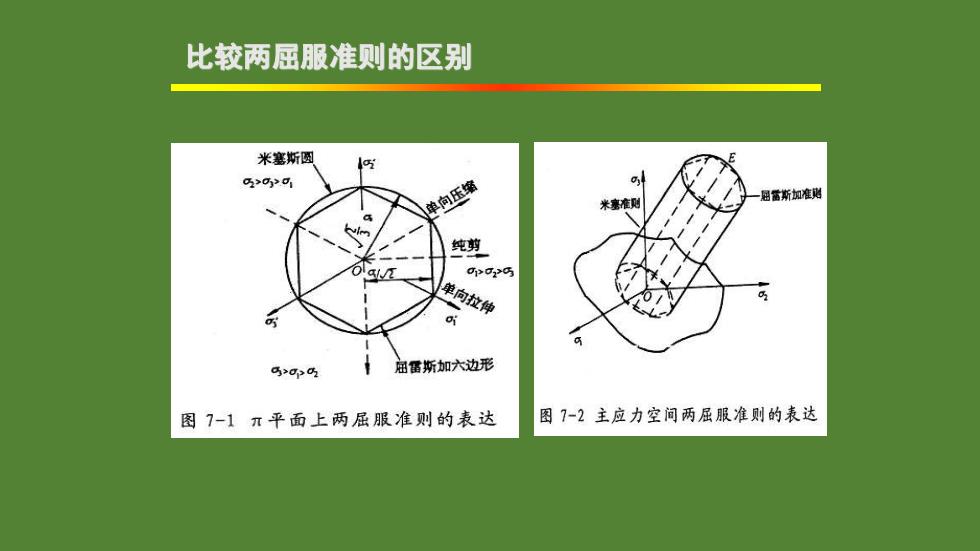
比较两屈服准则的区别 米塞斯圆 50>0 单向压缩 米塞则 冠雷斯加准斑 纯剪 单向拉伸 a>a 屈留斯加六边形 图7-1π平面上两屈服准则的表达 图?-2主应力空间两屈服准则的表达
比较两屈服准则的区别

两准则的联系: (1)空间几何表达:Mises圆柱外接于Tresca六棱柱; 在π平面上两准则有六点重合; (2) 通过引入罗德参数和中间主应力影响系数B,可以将两 准则写成 相同的形式: 01-O3=Bo B= 2 其中 √3+居 称为中间主应力影响系数 202-01-03 01-03 称为Lode参数
两准则的联系: (1)空间几何表达:Mises圆柱外接于Tresca六棱柱; 在π平面上两准则有六点重合; (2)通过引入罗德参数和中间主应力影响系数β,可以将两 准则写成 相同的形式: 其中 称为中间主应力影响系数 称为Lode参数。 1 3 − = s 2 2 3 = + 213 1 3 2 − − = −

讨论:①当材料受单向应力时,B=1,两准则重合; ②在纯剪应力作用下,两准则差别最大; 按Tresca准则: 无 按Mises?准则: 2 ③一般情况下,B=1-1.154
讨论:① 当材料受单向应力时,β=1,两准则重合; ② 在纯剪应力作用下,两准则差别最大; 按Tresca准则: 按Mises准则: ③ 一般情况下,β=1-1.154