
第20章光的干涉和衍射 §20.1光波的相干叠加 §20.2双缝干涉 §20.3薄膜干涉 §20.4偏振光的干涉 §20.5光的衍射 §20.6光栅衍射 §20.7圆孔衍射光学仪器的分辨本领 §20.8X射线的衍射
§20.1 光波的相干叠加 §20.3 薄膜干涉 §20.4 偏振光的干涉 §20.5 光的衍射 §20.6 光栅衍射 §20.7 圆孔衍射 光学仪器的分辨本领 §20.8 X射线的衍射 第 20 章 光的干涉和衍射 §20.2 双缝干涉
§20.6光栅衍射 光栅:由大量等宽、等间距的平行狭缝所组成的光学元件 透射光栅、反射光栅 a缝宽,b缝间距 d=a+b光栅常数 不考虑缝宽◆多缝干涉 sinWA I=Io 其中6= 2πdsin0令a=2 3 1=10J(c)
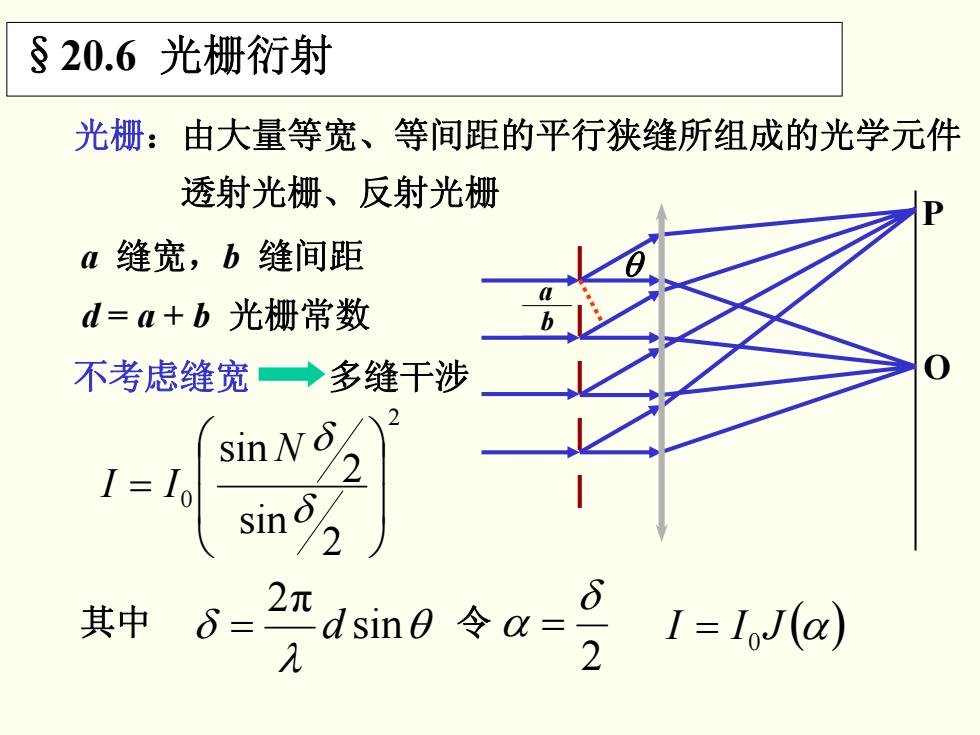
§20.6 光栅衍射 光栅:由大量等宽、等间距的平行狭缝所组成的光学元件 透射光栅、反射光栅 a b O P a 缝宽,b 缝间距 θ d = a + b 光栅常数 不考虑缝宽 多缝干涉 2 0 2 sin 2 sin ⎟⎟⎠⎞ ⎜⎜⎝⎛ = δ N δ II 其中 θ λ δ sin 2π = d 令 2 δ α = JII (α) = 0

2 光强分布 J(a)= sin Na sina =2 sin Na Neos Nasina-sin Nacosa 令 =0 da sina sin 2 sin Na (1) sina =0一e=ta{好2 此时J=0极小(零光强) Na=W0=m'元,.N6=2m'元 2 各点源发出的光的振幅矢量在P点 形成一封闭图形,合矢量为零
( ) 2 sin sin ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = α α α N J 0 sin cossinsincos sin sin 2 d d 2 = − ⋅= α α α α α α α α NNNJ N 令 光强分布 ( 1 ) 0 sin sin = α Nα α = ±mN ′π m′ = ,2,1 L ′ ≠ NNm ,2, L 此时J = 0 极小(零光强) π 2, π 2 == ′ δ =∴ mNmNN ′ δ Q α π 2 N m′ δ = 各点源发出的光的振幅矢量在 P 点 形成一封闭图形,合矢量为零

(2)Ntana tanNa 当a=±mmm=0,12,…时上式成立 此时J=N2,1=红,→主极大 28=2mm 条纹规律 相邻主极大△a=(m+1)m-mm=元 m'+1 m 相邻极小 △C= NN -2 sin Na Ncos Nasina-sin Nacosa da sina sin a
(2) 0 sin cossinsincos sin sin 2 d d 2 = − ⋅= α α α α α α α α NNNJ N N α = tantan Nα 当 α ±= mπ m = ,2,1,0 L 时上式成立 此时J = N2,I = N2I0 主极大 2, π 2 δ =∴= m δ Qα 条纹规律 相邻主极大 Δα = ( +1) − mm = πππ 相邻极小 NN m N m π ππ 1 = ′ − ′ + α =Δ
在相邻两主极大a=mπ,=(m+1)π之间,极小 (零光强)所对应的a为: 元 2元 N-1 mi+ mm卡 N …,mm+ 共N-1个。 N 而相邻两个极小之间必然还会出现极大一次极大。 次极大的数目为:N-2个 _元dsin0~6 对应不同角位置日,屏上交替出 .0= 2 现极大、极小
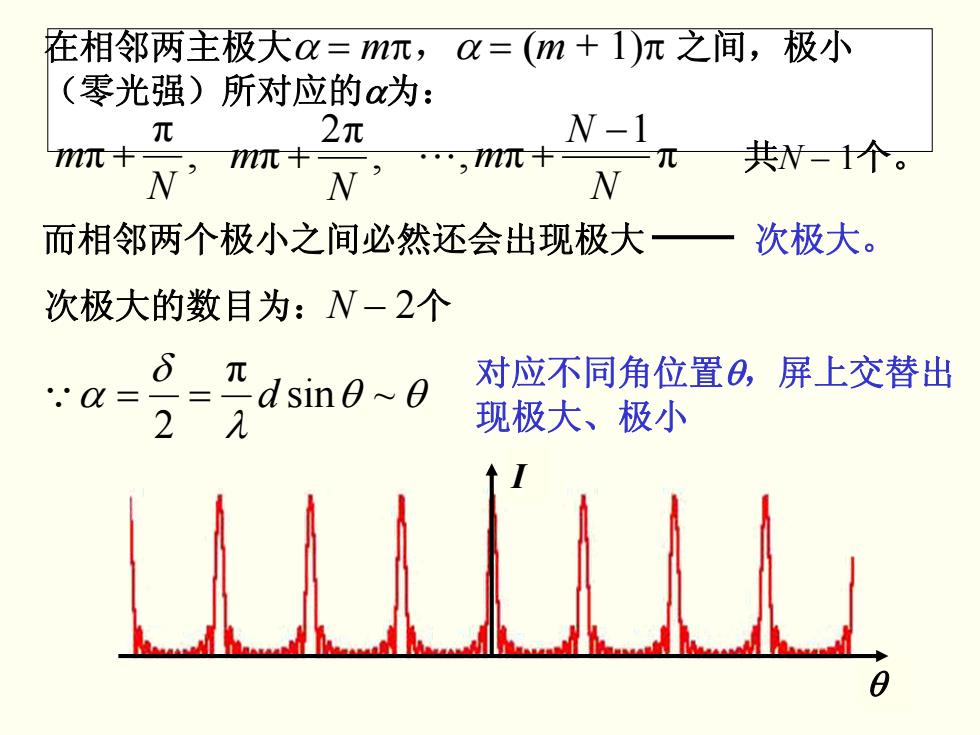
在相邻两主极大α = mπ,α = (m + 1)π 之间,极小 (零光强)所对应的α为: , π π N m + , 2π π N m + π 1 , π N N m − L + 共N – 1个。 θθ λ δ α ~sin π 2 Q == d 对应不同角位置θ,屏上交替出 现极大、极小 而相邻两个极小之间必然还会出现极大 次极大。 次极大的数目为:N – 2个 θ I