
10 10 12 2 5 5 5 6 00 6 00 12 12 20 20 14 14 6 7 3 13 SA SA 18 18 2 2020/12/08 6
2020/12/08 6

严格的数学模型-Flow Network A.flow network G=(V,E)is adirected graph in which each edge (u,v)EE has a nonnegative capacity c(u,v)=0.We further require that if E contains an edge (u,v),then there is no edge (v,u)in the reverse direction.(We shall see shortly how to work around this restriction.)If (u,v)E,then for convenience we define c(u,v)=0,and we disallow self-loops.We distinguish two vertices in a flow network:a source s and a sink t.For convenience,we assume that each vertex lies on some path from the source to the sink.That is,for each vertex v eV, the flow network contains a path svt.The graph is therefore connected and,since each vertex other than s has at least one entering edge,EV-1. 2020/12/08
严格的数学模型- Flow Network 2020/12/08 7

严格的数学模型-FloW We are now ready to define flows more formally.Let G =(V.E)be a flow network with a capacity function c.Let s be the source of the network,and let t be the sink.A flow in G is a real-valued function f:Vx V->R that satisfies the following two properties: Capacity constraint: Flow conservation: When (u.v)E,there can be no flow from u to v,and f(u.v)=0. 2020/12/08
严格的数学模型-Flow 2020/12/08 8

问题4: 什么叫一个flow的“value”? IfI=∑fs,)-∑fw,s) vEV vey 什么是最大流问题? 2020/12/08
问题4: 什么叫一个flow的“value”? 什么是最大流问题? 2020/12/08 9
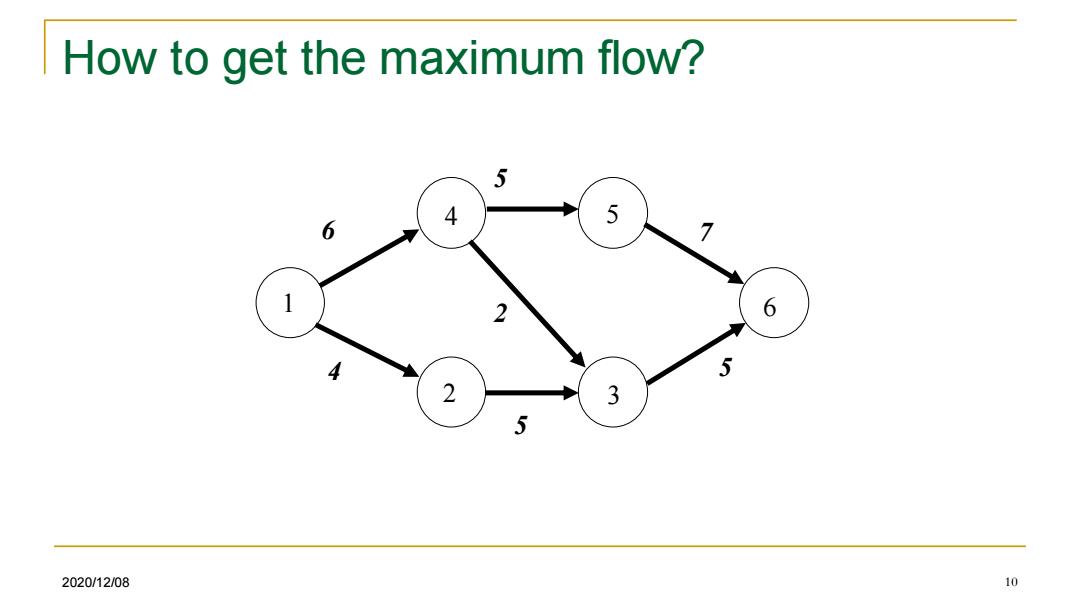
How to get the maximum flow? 5 4 5 6 2 6 4 5 2 3 5 2020/12/08 10
How to get the maximum flow? 6 4 5 2 3 1 5 5 4 7 5 6 2 2020/12/08 10