例:真空中有一均匀带电直线长为L,总电量为g,试 计算距直线距离为a的P点的场强.已知P点和直线两端 的连线与直线之间的夹角分别为0和02,如图所示. 解:步骤: 1.建立坐标,选电荷元 dq=Adx d 2.确定E的大小和方向 12c de 4元6 dx 3.将dE投影到坐标轴上 dE.=dE cos(180°-0) dE dE sin 两的肉例
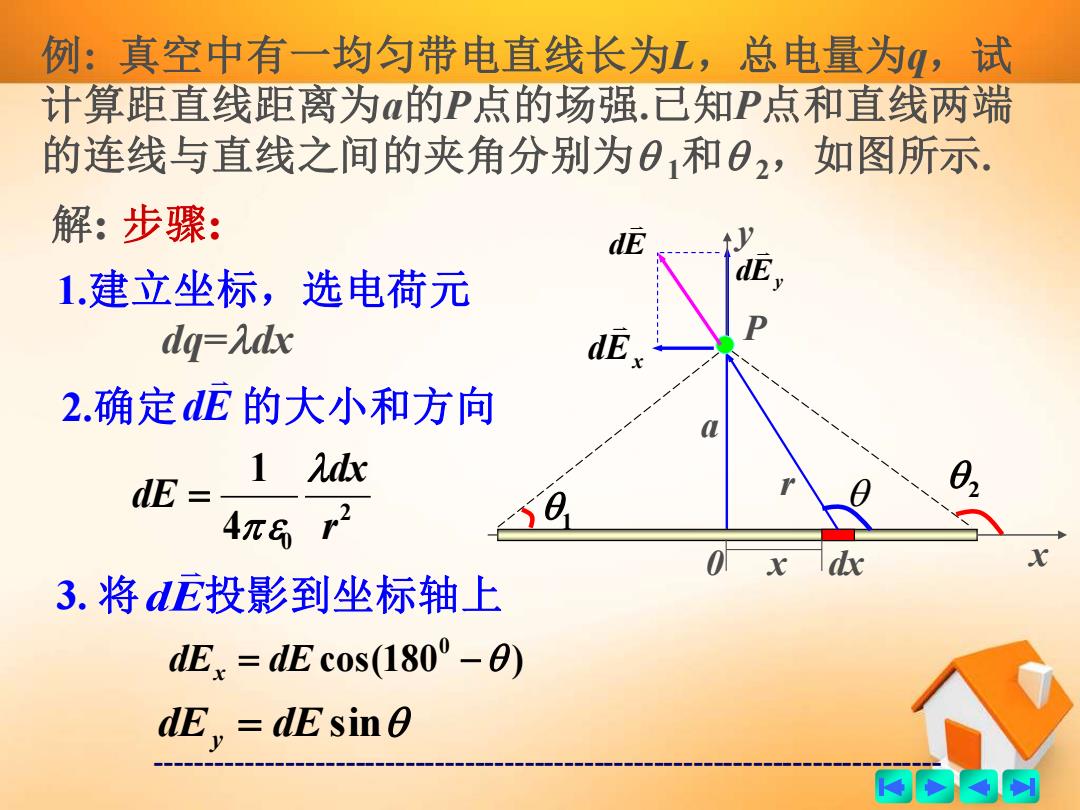
------------------------------------------------------------------------------- 例: 真空中有一均匀带电直线长为L,总电量为q,试 计算距直线距离为a的P点的场强.已知P点和直线两端 的连线与直线之间的夹角分别为 1和 2,如图所示. Ex d dEy x y 0 a 1 2 P x dx 解: 步骤: 1.建立坐标,选电荷元 dq=dx 2.确定 dE 的大小和方向 dE r 2 0 4 1 r dx dE = 3. 将 dE 投影到坐标轴上 cos(180 ) 0 dEx = dE − dEy = dE sin
4.选择适当的积分变量 d厄 r、0、x三变量选 一个积分变量 dE 选0作为积分变量, L 因此 a 2= sin20 X x-a-(g(0-)--actg0 de dx=a sin20 元cos0d0 .dE.=4π 2 E,= sin0de 4元0 商的内网
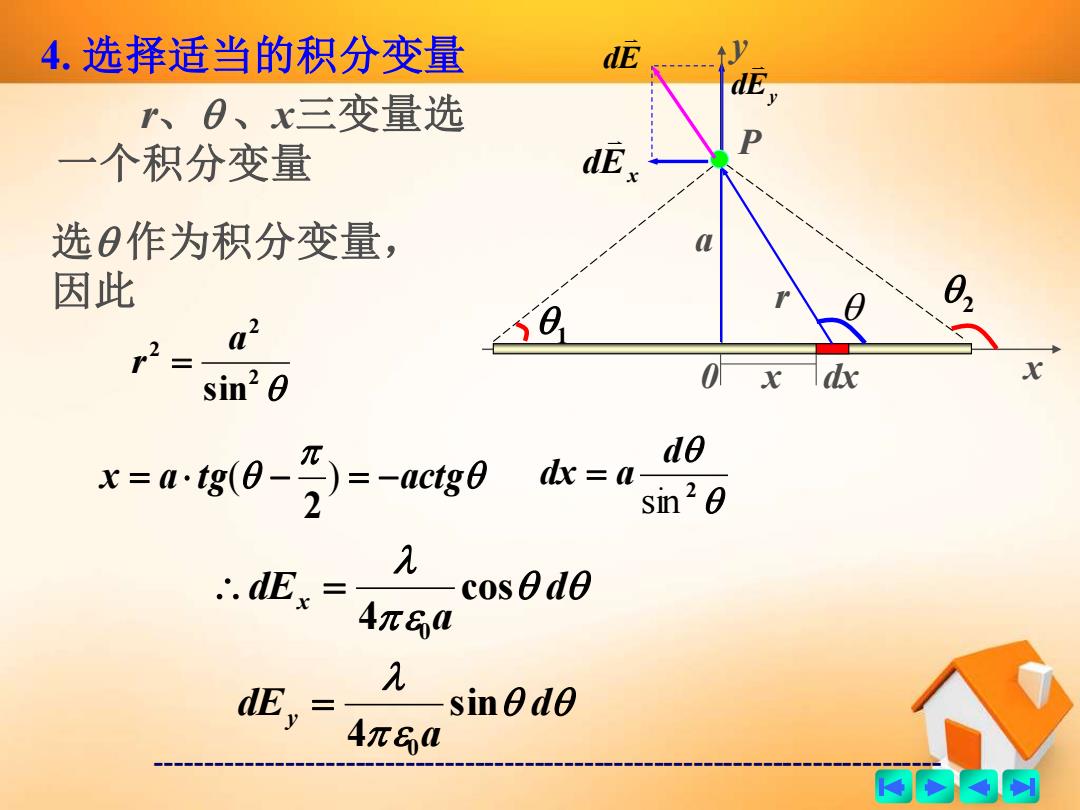
------------------------------------------------------------------------------- 4. 选择适当的积分变量 dEx Ey d x y 0 a 1 2 P x dx dE r r、 、x三变量选 一个积分变量 选 作为积分变量, 因此 2 2 2 sin a r = x = a t g( − ) = −actg 2 2 sin d dx = a d a dEx cos 4 0 = d a dEy sin 4 0 =

E.-∫,医--n (sine-sing) -小匹,r广如g= (cos0-cos2) 讨论: ·当直线长度L→00,或→0,则 0→0,82→元 E.=0 E,=2r80 •当入异号时,E方向相反 粉南厨
------------------------------------------------------------------------------- d a Ex dEx cos 4 2 1 0 = = ( ) 2 1 0 sin sin 4 = − a = = 2 1 sin 4 0 d a E dE L y y (cos cos ) 1 2 0 4 = − a 讨论: •当直线长度L→∞,或a→0,则 1→0, 2→ Ex = 0 j a Ey 2 0 = E r j r E 2 0 = •当异号时,E方向相反

六、带电体在外电场中所受的作用 F=gE F=∫Edg 讨论:如图已知±q、d、S 求两板间的所用力 d 4 f=42828S +4 -4 91 4π6od2 商的内网
------------------------------------------------------------------------------- 六、带电体在外电场中所受的作用 F qE = F = Edq 讨论:如图已知q、d、S 求两板间的所用力 + q − q d S q f q 0 2 0 2 2 = = 2 0 2 4 d q f

电偶极子在外电场中受的力和力矩 合力 F-F.+F=0 十9F=+E 合力矩 +E MFsin+FsinO-QlEsin0 M=p×E 可见:p⊥E力矩最大;D∥E力矩最小。 力矩总是使电矩p转向E的方向,以达到稳定状态 两的肉例
------------------------------------------------------------------------------- 电偶极子在外电场中受的力和力矩 F+ = +qE F− = −qE + q E − q o F = F+ + F− = 0 合 力 sin sin 2 sin 2 qlE l F l M = F+ + − = 合力矩 M p E = 力矩总是使电矩 p 转向 的方向,以达到稳定状态 E 可见: p E 力矩最大; 力矩最小。 ⊥ p E //