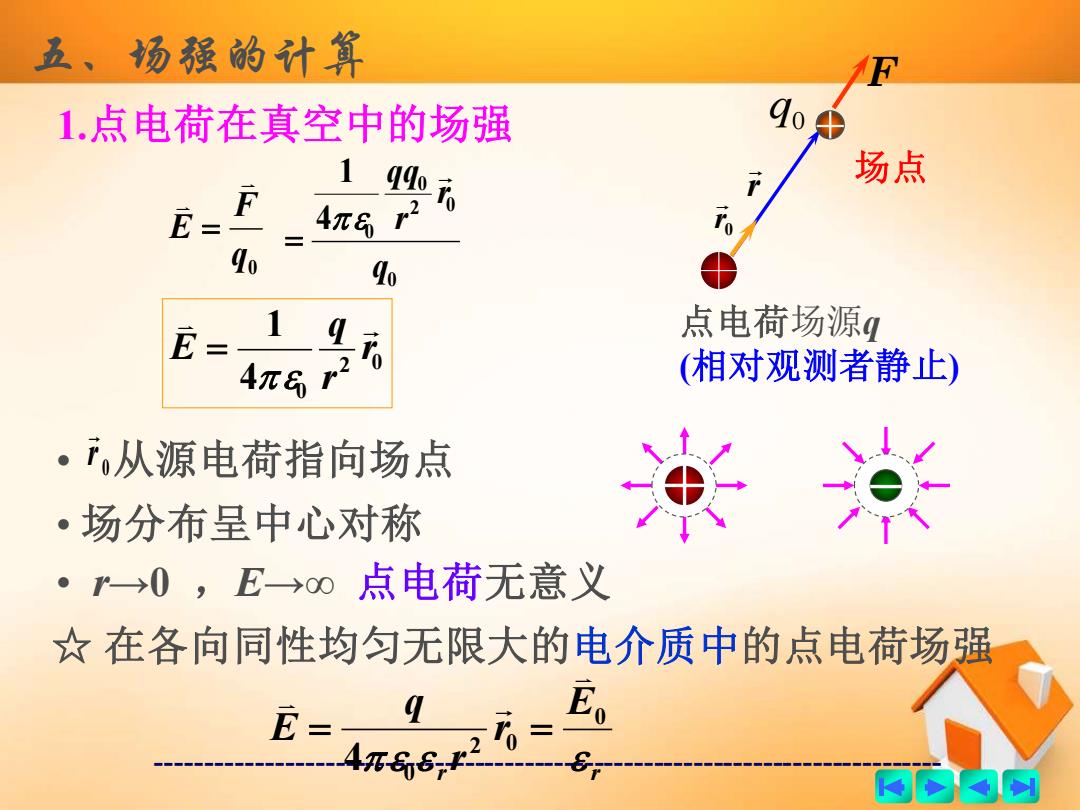
五、场强的计算 1.点电荷在真空中的场强 1 q46 场点 2 E= F 4π6 40 90 1 点电荷场源q 4π6r (相对观测者静止) 。从源电荷指向场点 ·场分布呈中心对称 汝米 ·”0,E0点电荷无意义 ☆在各向同性均匀无限大的电介质中的点电荷场强 龙=, 西的南的
------------------------------------------------------------------------------- 五、场强的计算 1.点电荷在真空中的场强 点电荷场源q (相对观测者静止) r 场点 0 r q0 F 0 q F E = 0 2 0 0 0 4 1 q r r qq = 2 0 4 0 1 r r q E = • r 0 从源电荷指向场点 • 场分布呈中心对称 • r→0 ,E→∞ 点电荷无意义 ☆ 在各向同性均匀无限大的电介质中的点电荷场强 r r E r r q E 0 2 0 0 4 = =
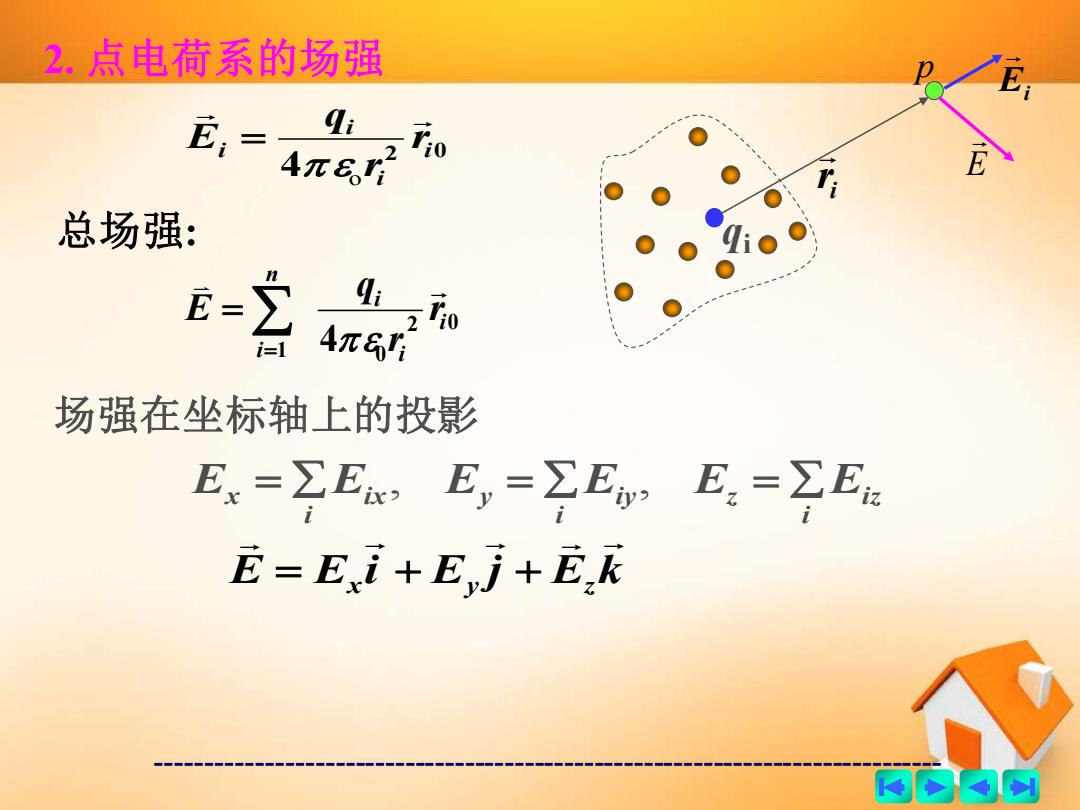
2.点电荷系的场强 E=和 总场强: E=立 场强在坐标轴上的投影 Ex=∑Ex,E,=∑E,E.=∑Ea E=Ei+Ej+Ek 两的肉厨
------------------------------------------------------------------------------- 2. 点电荷系的场强 p i r qi Ei 2 0 4 i i i i r r q E o = 总场强: 2 0 1 0 4 i i i n i r r q E = = E i z i i y z i i x y i Ex = E , E = E , E = E 场强在坐标轴上的投影 E Ex i Ey j Ez k = + +

3连续带电体的电场 dq dE E=∫ 注意:上式为矢量体积分. 电荷元随不同的电荷分布应表达为 体电荷分布dq=pdW 面电荷分布dg=σdS 线电荷分布dg=2dl E=E:E,=∫E,E=∫E E=Ei+E j+Ek 商的内网
------------------------------------------------------------------------------- 3.连续带电体的电场 dq E d p 0 r 2 0 4 0 r r dq dE = 2 0 0 4 1 r r dq E dE = = 注意:上式为矢量体积分. 电荷元随不同的电荷分布应表达为 体电荷分布 dq= dV 面电荷分布 dq= dS 线电荷分布 dq= dl x = x y = y z = z E dE E dE E dE E Ex i Ey j Ez k = + +
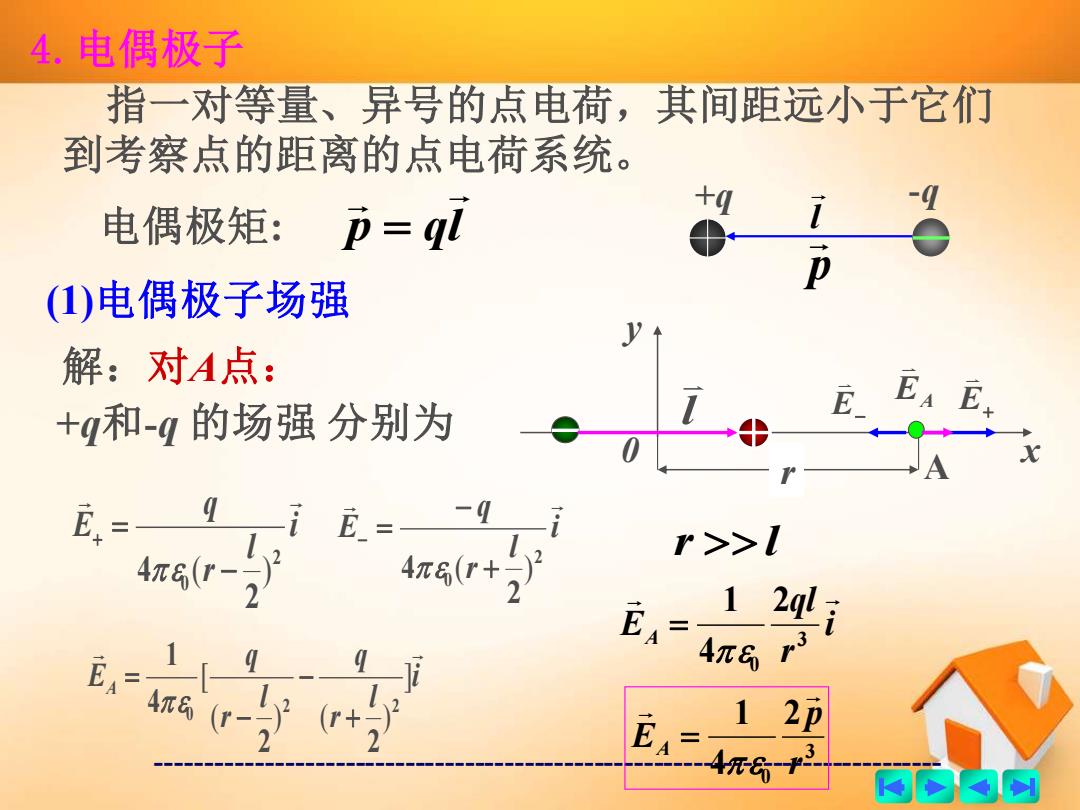
4.电偶极子 指一对等量、异号的点电荷,其间距远小于它们 到考察点的距离的点电荷系统。 -4 电偶极矩:p=ql +4 i e p (1)电偶极子场强 解:对A点: +q和-4的场强分别为 E EA iE.=- -4 + r>>l 124i 12 雨的卤例
------------------------------------------------------------------------------- 4.电偶极子 指一对等量、异号的点电荷,其间距远小于它们 到考察点的距离的点电荷系统。 +q -q 电偶极矩: l p p ql = (1)电偶极子场强 解:对A点: y l 0 r A x +q和-q 的场强 分别为 E+ i l r q E 2 0 2 4 ( − ) = + E− i l r q E 2 0 2 4 ( + ) − − = EA i l r q l r q EA ] ( ) ( ) [ 2 2 0 2 2 4 1 + − − = r l i r ql EA 3 0 2 4 1 = 3 0 2 4 1 r p EA =
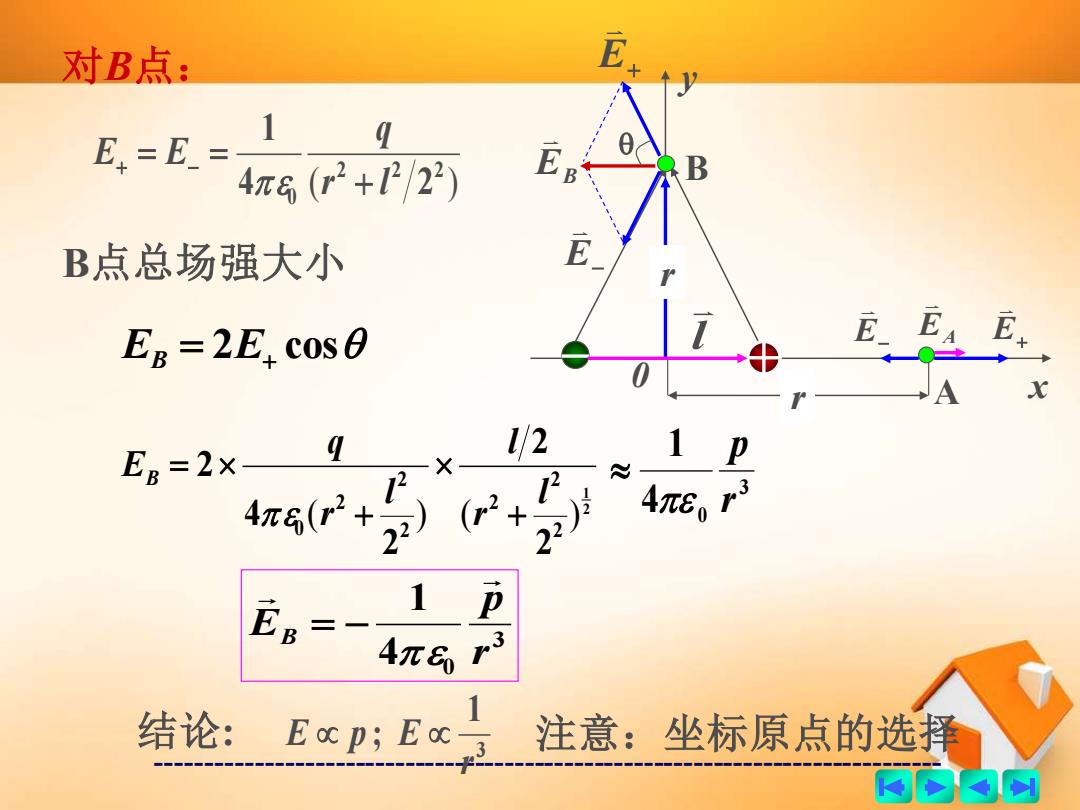
对B点: 1 E,=E.=4坏62+2) E B点总场强大小 E EB =2E,COS0 E.EE 0 A EB=2X— L/2 1 P 4πe,3 1 p 4π8r3 结论: Ec卫;Ec月 。1 注意:坐标原点的选择 的内例
------------------------------------------------------------------------------- 对B点: E+ E− EA B r y l E+ E− 0 r A x ( ) 2 2 2 0 4 2 1 r l q E E + + = − = B点总场强大小 EB EB = 2E+ cos 2 1 2 2 2 2 2 2 0 2 2 2 4 2 ( ) ( ) l r l l r q EB + + = 3 0 4 1 r p 3 4 0 1 r p EB = − 结论: 3 1 ; r E p E 注意:坐标原点的选择