1.小波介绍一小波分析(续2) CWT的变换过程示例, 见右图,可分如下5步 1.小波()和原始信号)的 开始部分进行比较 2.计算系数C一该部分信号 与小波的近似程度;C值 平移 w(t 越高表示信号与小波相似 w(t-k) 程度越高 v(t-2k) 平移 3.小波右移得到的小波函数 v(t-3k) 为y(t-),然后重复步骤1 和2,...直到信号结束 4. 扩展小波,如扩展一倍, 得到的小波函数为y(t/2) 5.重复步骤14 连续小波变换的过程
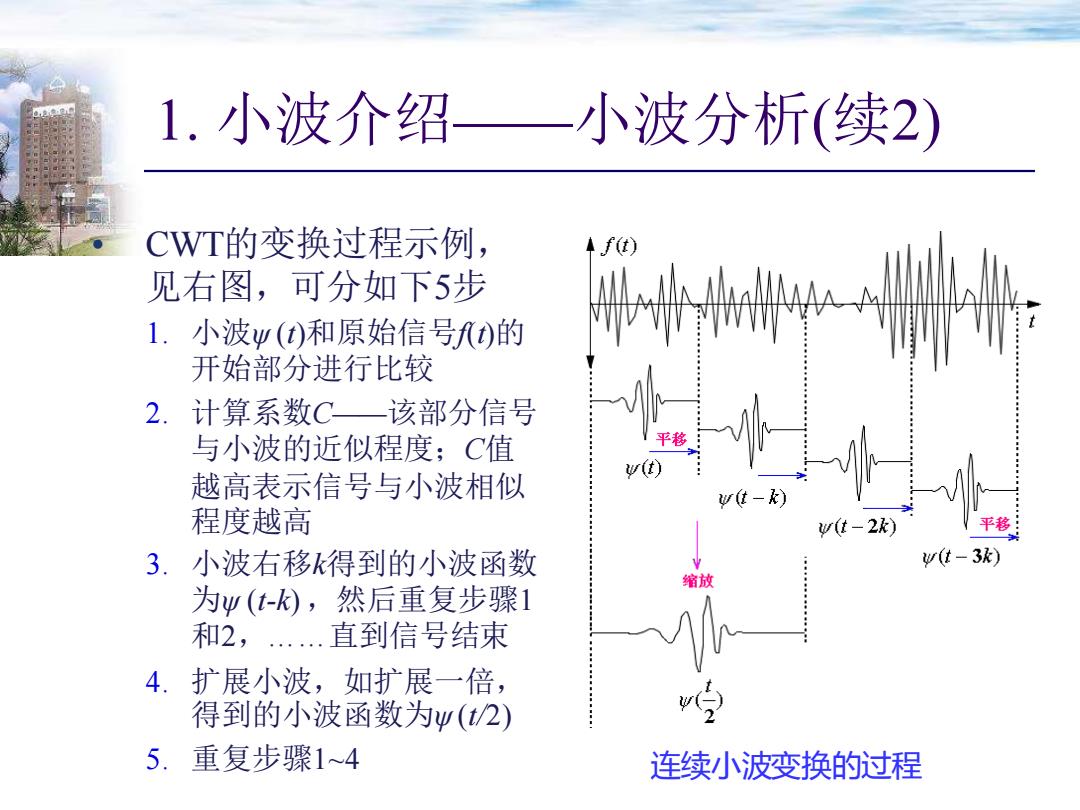
1. 小波介绍——小波分析(续2) • CWT的变换过程示例, 见右图,可分如下5步 1. 小波ψ (t)和原始信号f(t)的 开始部分进行比较 2. 计算系数C——该部分信号 与小波的近似程度;C值 越高表示信号与小波相似 程度越高 3. 小波右移k得到的小波函数 为ψ (t-k) ,然后重复步骤1 和2,……直到信号结束 4. 扩展小波,如扩展一倍, 得到的小波函数为ψ (t/2) 5. 重复步骤1~4 连续小波变换的过程

1.小波介绍一小波分析(续3) 连续小波变换用下式表示 C(scale,position)=f(t)(scale,position,t)dt 该式含义:小波变换是信号)与被缩放和平移的小波函数平之 积在信号存在的整个期间里求和 CWT变换的结果是许多小波系数C,这些系数是缩放因子(scale) 和位置(position)的函数 离散小波变换(discrete wavelet transform,DWT) 用小波的基函数(basis functions)表示一个函数的方法 小波的基函数序列或称子小波baby wavelets)函数是由单个小波 或称为母小波函数通过缩放和平移得到的 缩放因子和平移参数都选择20>0的整数)的倍数,这种变换称 为双尺度小波变换(dyadic wavelet transform)
1. 小波介绍——小波分析(续3) • 连续小波变换用下式表示 C scale position f t scale position t dt ( , ) ( ) ( , , ) + − = ◼ 该式含义:小波变换是信号f(t)与被缩放和平移的小波函数Ψ之 积在信号存在的整个期间里求和 ◼ CWT变换的结果是许多小波系数C ,这些系数是缩放因子(scale) 和位置(position)的函数 ◼ 离散小波变换(discrete wavelet transform,DWT) ➢ 用小波的基函数(basis functions)表示一个函数的方法 ◼ 小波的基函数序列或称子小波(baby wavelets)函数是由单个小波 或称为母小波函数通过缩放和平移得到的 ◼ 缩放因子和平移参数都选择2 j (j >0的整数)的倍数,这种变换称 为双尺度小波变换(dyadic wavelet transform)
1.小波介绍一小波分析(续4) DWT得到的小波系数、缩放因子和时间关系 图(a)是20世纪40年代使用Gabor?开发的短时傅立叶变换(short time Fourier transform,STFT)得到的 ·图(b)是20世纪80年代使用Morleti开发的小波变换得到的 w: Mi S3 (a)STFT (b)CWT 离散小波变换分析图
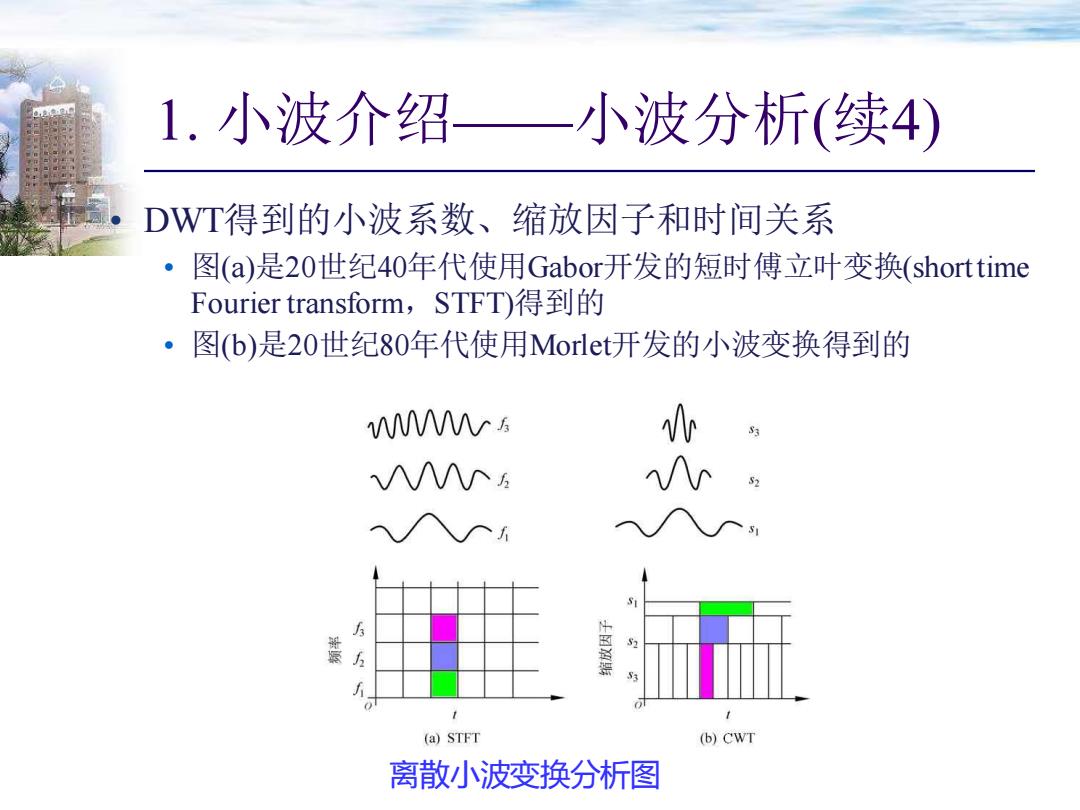
1. 小波介绍——小波分析(续4) 离散小波变换分析图 • DWT得到的小波系数、缩放因子和时间关系 • 图(a)是20世纪40年代使用Gabor开发的短时傅立叶变换(short time Fourier transform,STFT)得到的 • 图(b)是20世纪80年代使用Morlet开发的小波变换得到的
1.小波介绍一小波分析(续5) 执行DWT的有效方法 ·用Mallat在l988年开发的滤波器,称为Mallat算法 DWT的概念见下图。S表示原始的输入信号;通过两 个互补的滤波器产生A和D两个信号 ■A表示信号的近似值 approximations),大 的缩放因子产生的系 滤波器 低通 高通 数,表示信号的低频 芬量 D表示信号的细节值 (detail),小的缩放因 子产生的系数表宗 双通道滤波过程 信号的高频分量
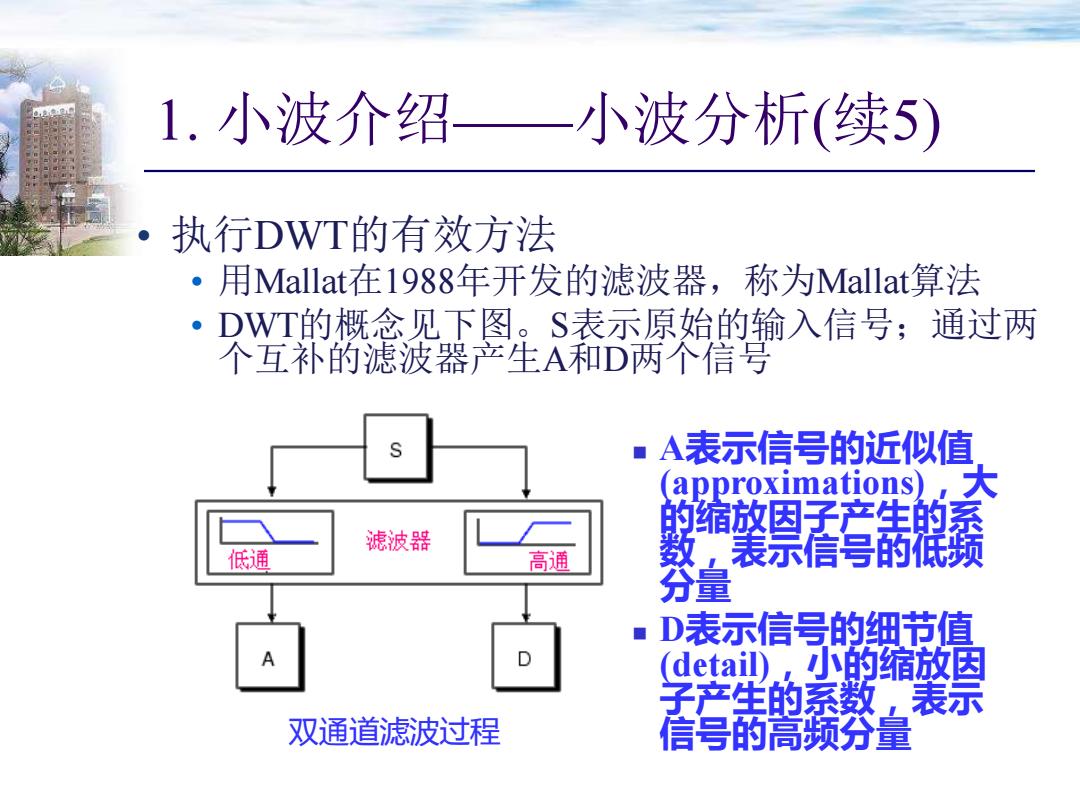
1. 小波介绍——小波分析(续5) • 执行DWT的有效方法 • 用Mallat在1988年开发的滤波器,称为Mallat算法 • DWT的概念见下图。S表示原始的输入信号;通过两 个互补的滤波器产生A和D两个信号 双通道滤波过程 ◼ A表示信号的近似值 (approximations),大 的缩放因子产生的系 数,表示信号的低频 分量 ◼ D表示信号的细节值 (detail),小的缩放因 子产生的系数,表示 信号的高频分量

1.小波介绍一小波分析(续6) ,小波分解树与小波包分解树 ·由低通滤波器和高通滤波器组成的树 ·原始信号通过一对滤波器进行的分解叫做一级分解。信 号的分解过程可以迭代,即可进行多级分解, 。小波分解树(wavelet decomposition tree) ·用下述方法分解形成的树:对信号的高频分量不再继续 分解,而对低频分量连续进行分解,得到许多分辨率较 低的低频分量 ·小波包分解树(wavelet packet decomposition tree) ·用下述方法分解形成的树:不仅对信号的低频分量连续 进行分解,而且对高频分量也进行连续分解,这样不仅 可得到许多分辨率较低的低频分量,而且也可得到许多 分辨率较低的高频分量
1. 小波介绍——小波分析(续6) • 小波分解树与小波包分解树 • 由低通滤波器和高通滤波器组成的树 • 原始信号通过一对滤波器进行的分解叫做一级分解。信 号的分解过程可以迭代,即可进行多级分解. • 小波分解树(wavelet decomposition tree) • 用下述方法分解形成的树:对信号的高频分量不再继续 分解,而对低频分量连续进行分解,得到许多分辨率较 低的低频分量. • 小波包分解树(wavelet packet decomposition tree) • 用下述方法分解形成的树:不仅对信号的低频分量连续 进行分解,而且对高频分量也进行连续分解,这样不仅 可得到许多分辨率较低的低频分量,而且也可得到许多 分辨率较低的高频分量