
省级精品课程一材料力学 拉伸变形时,杆的纵向伸长,横向缩短;压缩变形时,杆的纵向缩短,横向 伸长。也即,拉(压)杆的横向变形与纵向变形性质相反。记,兰称为横向 应变,实验表明,在弹性范围内,同一材料的横向应变与纵向应变之比为一常数, (2-15) 山称为横向变形系数,也称为泊松比,它是一个材料常数。 几种常用材料的E、u值见表2-1。 表2-1弹性模量E和泊松比u的约值 材料名称 E(GPa) 碳钢 200~220 0.24~0.30 合金钢 200210 0.250.32 灰口铸铁 60162 0.230.27 球墨铸铁 150~180 0.24-0.27 铝及其合金 70~72 0.26-0.36 钢及其合金 100~110 0310.36 混凝土(100~400号) 1526 0.16~0.2 木材(顺纹) 912 木材(横纹) 0.5~1 石料 6-9 0.16-0.28 2.73.5 0.12~0.20 橡 0.008-0.67 0.47 例2-6: 正方形截面的阶梯砖柱,如图2-17所示。已知材料的弹性模量E=3 Ga,试求砖柱顶面的位移6,设砖柱的基础没有沉陷。 解:当砖柱的基础没有沉路时,砖柱顶面的位移等于砖 ,P=50W 柱的缩短。砖柱两段的轴力分别为N,=50KN(压),N,=150K (压),故 ☆☆ 6=+,= 50×10×3 3×10'×0.25 =2.26×10m=2.26m(向下) □ 因27 例2-7:图2-18(a)所示为钢杆1和2组成的铰接结构,在节点A处悬挂一重 物P=100K\,两钢杆的长度L及直径d都相同,已知钢的弹性模量E=210GPa, 试求节点A的位移 解:首先计算两杆的轴力。对节点A列平衡方程,见图2-18(b), This document is generated by trial version of Print2Flash(www.print2flash.com)
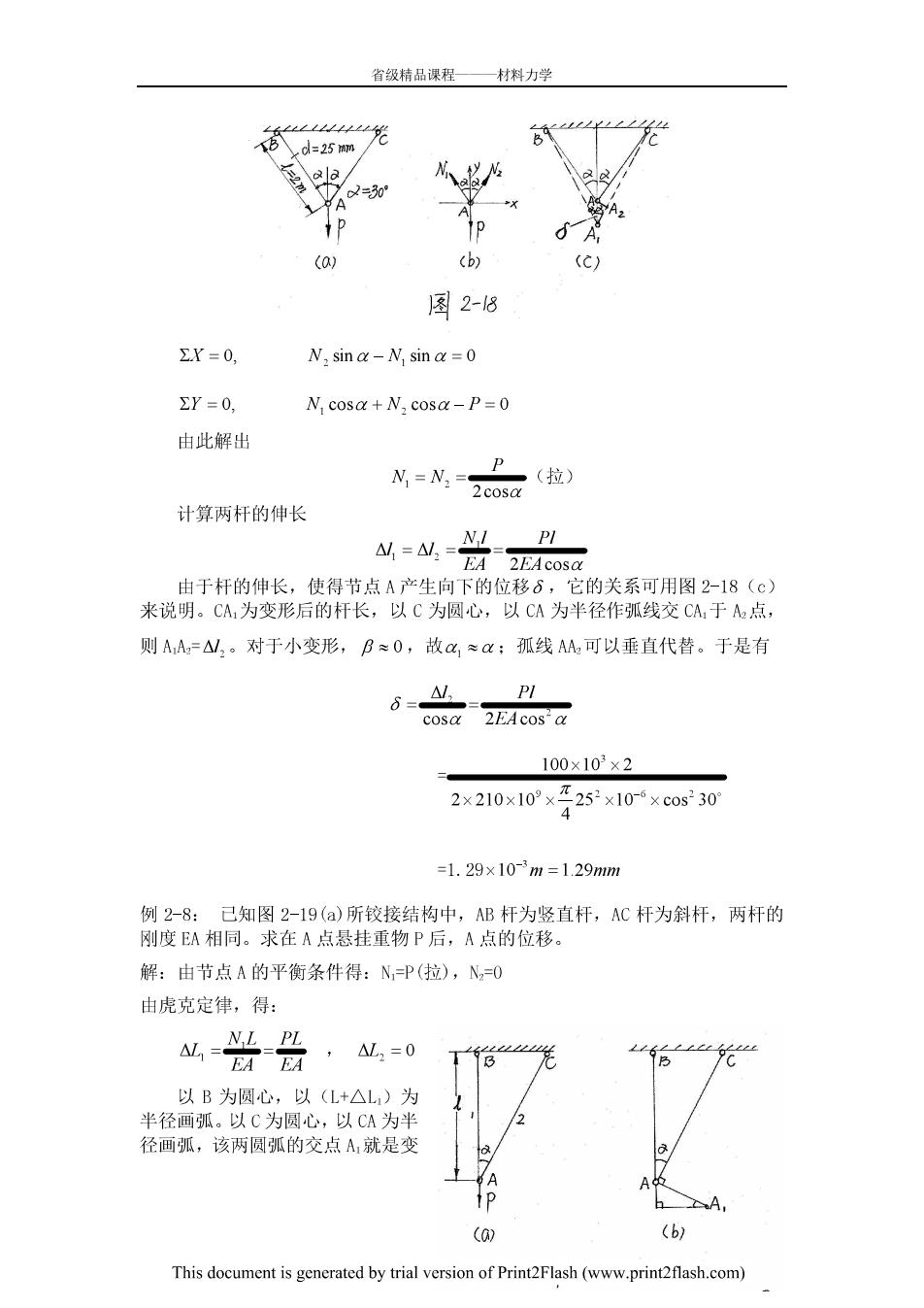
省级精品课程 一材料力学 d=25m (b) c 图2-8 Y=0, N,sin a-N sin a=0 Y=0, N cosa+N:cosa-P=0 由此解出 N=N=20a(拉) P 计算两杆的伸长 EA 2EAcosa 由于杆的伸长,使得节点A产生向下的位移6,它的关系可用图2-18(c》 来说明。CA,为变形后的杆长,以C为圆心,以CA为半径作弧线交CA,于A点, 则AA=△,。对于小变形,B≈0,故≈:孤线AM可以垂直代替。于是有 6= cosa 2EAcos'a 100×103×2 2×210x102×Z252x10-×c0s230 =1.29×103m=1.29mn 例2-8:已知图2-19(a)所铰接结构中,AB杆为竖直杆,AC杆为斜杆,两杆的 刚度EA相同。求在A点悬挂重物P后,A点的位移 解:由节点A的平衡条件得:N,=P(拉),N,O 由虎克定律,得 ,L2=0 以B为圆心,以(L+△L)为 半径画弧。以C为圆心,以CA为半 径画弧,该两圆弧的交点A就是变 (b) This document is gencrated by trial version of Print2Flash (www.print2flash.com)