
省级精品课程—材料力学 第十三章能量法 §13.1基本概念 一、能量原理 在固体力学中,有许多与能量概念有关的定理、原理。例如,所谓功能原理就是其中的 一个。图13-l(a)所示的梁就是变形周体,在外力P的作用下,力的作用点沿力的作用线 方向产生位移△,于是外力P作了功。与此同时,桑由于变形而储存了变形能。若外力》 零开始缓慢平稳地增加到最终值,在变形过程中,动能及热能的变化可以略去不计,于是可 以认为,外力所做的功W全部转化为储存于变形周体内的变形能U,即 U-W (13-1) P IR ) (b) 图13-1 (13-1)式称为功能原理,它实际上是能量守恒与转换定律在变形固体中的一个具体应用。 理论力学中介绍的虚功原理也是一个例子。这里不打算重复虚功原理的内容,但为了后 面使用方便,必须强调一下虚功的概念在图13-(b)所示的梁上已有P力作用,若再作 用R力, 此时P力作用点沿P力方向产生了位移 2 因 力P在位移△:上也 了功。 在别的原因所产生的位移上微的功称为虚功,这里的位移当然是指力的作用点沿力的作用线 方向的位移.图13-1(b)中P力在△,上做的功就是虚功,而图13-1(a)中P力在△,做 的功是实功。 我们把与能量摄今有关的定理、原理续称为能量原理。因为功的表法式中总句含位移, 因此可以应用能量原理来计算变形固体的位移,这个方法称为能量法。实际上,能量法是计 算位移的普遍而又简便的方法。 二、基本变形时杆的弹性变形能 下面分别讨论杆在几种基本变形时的变形能。 1 轴向拉伸或压缩 在线弹性范用内,当拉力P从零开始逐渐增加到最终值时,杆的伸长△L与拉力P成线 性关系,见图 13-2(a)入、()。现在设想如同加砝码那样,拉力P是一点一点逐渐增加的 设在加载过程中拉力为P1,杆的伸长为△L,见图13-2(b)、(©).若拉力再增加P,则 伸长的增量为d(△L),此时己有的P1力在位移d(△)上所做的元功是 dw=Pd△L) 235 This document is generated by trial version of Print2Flash(www.printflash.com)
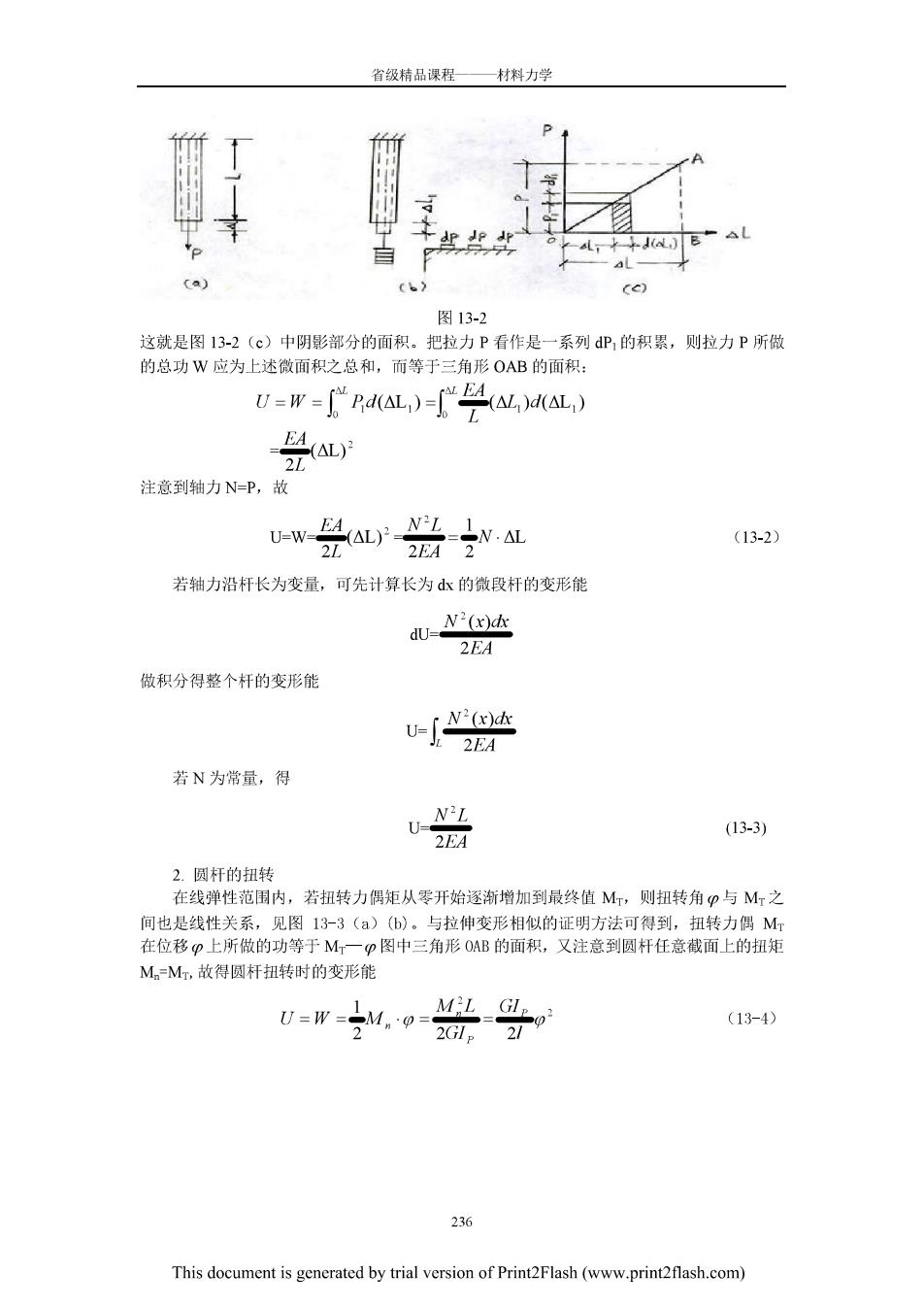
省领精品课程 一材料力学 ,+ L CL) 图13-2 这就是图13-2(c)中阴影部分的面积。把拉力P看作是一系列P1的积累,则拉力P所做 的总功W应为上述微面积之总和,而等于三角形OAB的面积: U=w-f广PdaL,-'兰uaL) EA(AL) 2L 注意到轴力N=P,故 (13-2) 2L 若轴力沿杆长为变量,可先计算长为止的微段杆的变形能 d-Ww达 2EA 做积分得整个杆的变形能 若N为常量,得 (13-3) 2.圆杆的扭转 在线弹性范围内,若扭转力偶矩从零开始逐新增加到最终值M,则扭转角0与M之 间也是线性关系,见图133(a)(b)。与拉伸变形相似的证明方法可得到,扭转力偶Mr 在位移P上所做的功等于M,一p图中三角形0OB的面积,又注意到圆杆任意截面上的扭矩 M,=M,故得圆杆扭转时的变形能 r器号 (13-4) 236 This document is gencrated by trial version of Print2Flash (www.printflash.com)
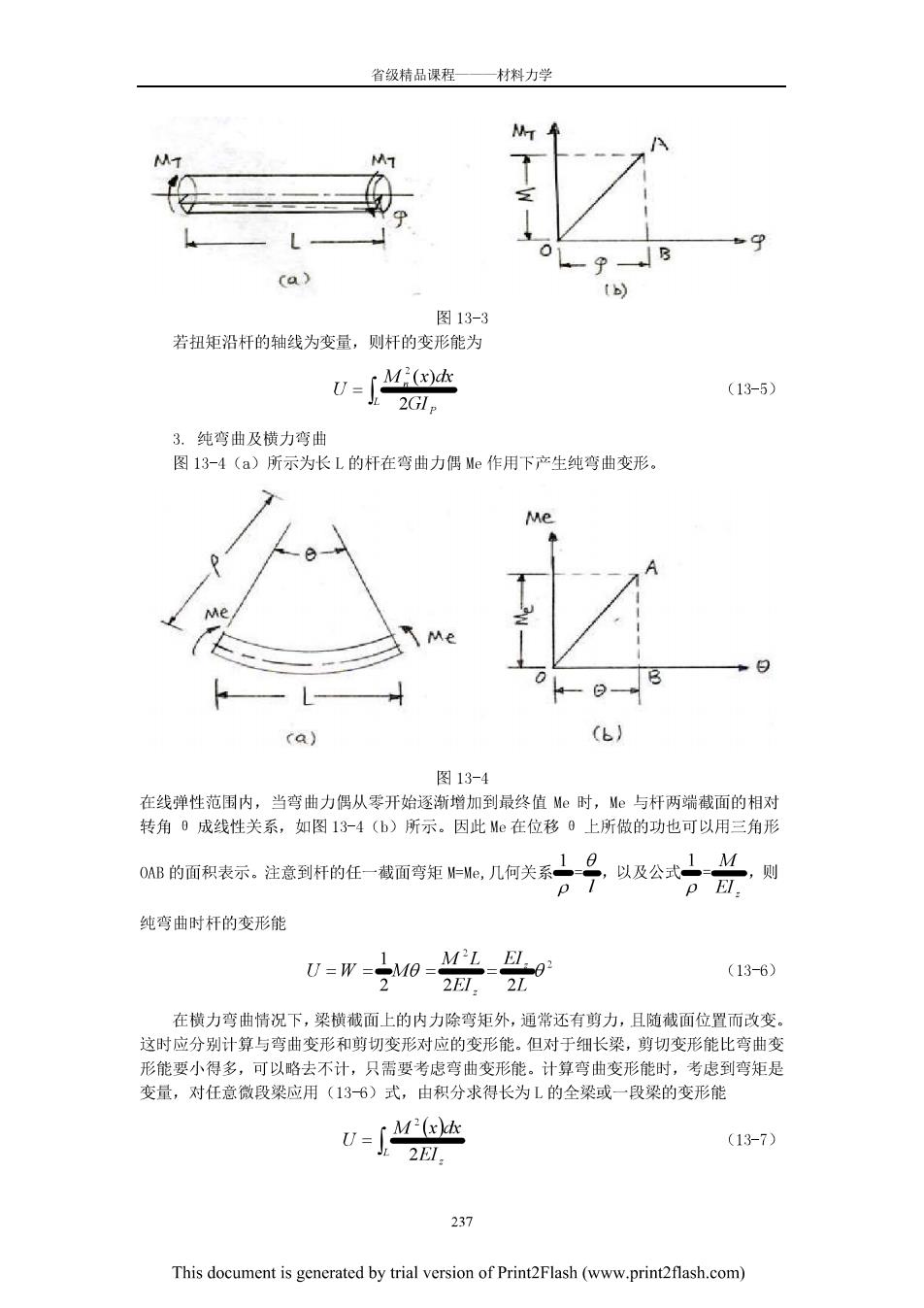
省级精品课程 一材料力学 (a) 图13-3 若扭矩沿杆的轴线为变量,则杆的变形能为 U=「Mx (13-5】 2G1. 3.纯弯曲及横力湾曲 图13-4(a)所示为长L的杆在弯曲力偶Me作用下产生纯弯曲变形, (a) (6) 图13-4 在线弹性范围内,当弯曲力偶从零开始逐渐增加到最终值Me时,e与杆两端截面的相对 转角成线性关系,如图13-4(b)所示。因此Me在位移上所做的功也可以用三角形 0的面积表示,法意到杆任一面矩,几何关系分子以及公式分 M,则 纯弯曲时杆的变形能 (13-6) 在横力弯曲情况下,梁横截面上的内力除弯矩外,通常还有剪力,且随截面位置而改变 这时应分别计算与弯曲变形和剪切变形对应的变形能。但对于细长染,剪切变形能比弯曲变 形能要小得多,可以略去不计,只需要考虑弯曲变形能。计算弯曲变形能时,考虑到弯矩是 变量,对任意微段梁应用(136)式,由积分求得长为L的全梁或一段梁的变形能 0=∫44 (13-7) 2EI, 237 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 综合以上讨论,在线弹性范围内,若外力由零开始逐渐增加到最终值,外力功等于力与 力作用点沿力方向位移的乘积的一半。根据功能原理,杆的变形能在数值上等于变形过程中 外力所做的功。因此可将变形能写成统一的形式 U-8-P5 (13-8) 这里P和6分别为广义力和广义位移。 三、组合变形时杆的弹性变形能 M(n K) 图13-5 设杆的某一微段同时存在弯曲、扭转和拉伸(压缩)变形,相应的内力弯矩M(x入、扭 矩M(x)和轴力N(x)如图135所示。设两端截面的相对转角为d0、相对扭角为d、相对 向位移为,△山.由于横藏面上内力只在相对应的位移上作功,在其他位移上不内 例如弯矩() 上作) 在扭角dp和 位科 作功,因此杆白 弯曲变形能、扭转变形能、拉(压)变形能可分别独立计算,并叠加作为组合变形时的变形 能: d=分N)d(△D+号n6d0+号L)dg N()d M()de M.()c 2EA 2EI, 2GIp 整个杆的变形能由积分得到 (13-9) 2EA 27 2G 四、变形能的性质 总结以上分析,弹性变形能有以下主要性质: 弹性变形能恒为正值,因为变形能总可表示为内力的平方或位移的平方,故恒 为正。 2 弹性变形能只与变形的初始状态和最终状态有关,而与变形的过程或加载的次 序无关。这个性质其实就是势能所具有的性质,弹性变形能也就是一种势能。还可以用反过 法来说明这个性质:假定弹性变形能与加载的次序有关,我们可以用一种次序加载,再卸载 (即用另一种次序加载),于是会多出净功,这不符合能量守恒原理。因此,假定是不正确 的。 弹性变形能的计算通常不适用叠加原理。理由很简单,因为变形能是内力或位 移的二次式。例如,设图13-6(a)所示的躁在P作用下的变形能为 U=4w达 2 238 This document is gencrated by trial version of Print2Flash (www.print2flash.com)
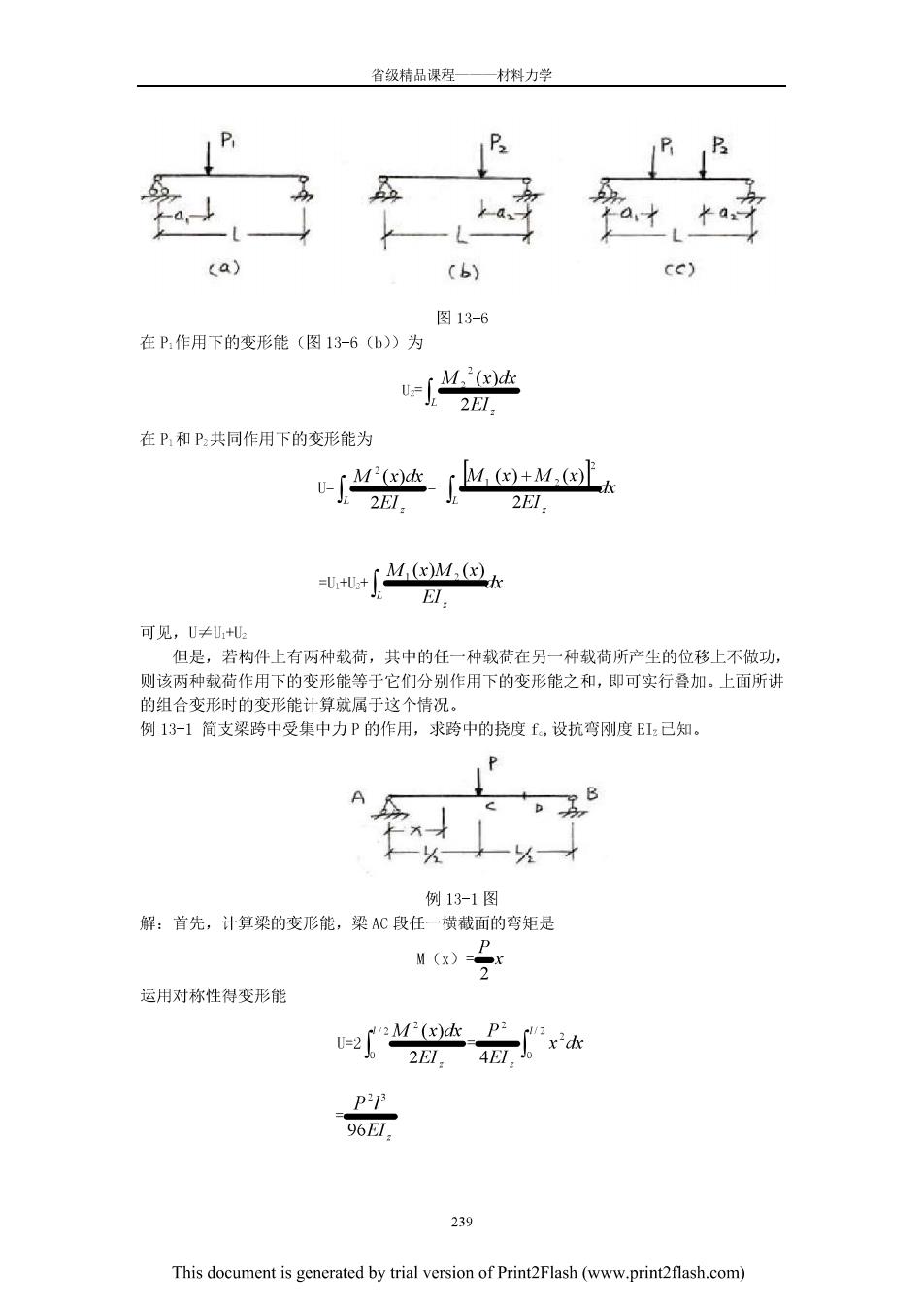
省领精品课程一材料力学 *a ta) (b) ce) 图13-6 在P作用下的变形能(图13-6(b)为 w达 在P和P共同作用下的变形能为 ∫M达 rM)+M.止 2E 2E1 w+∫(M.包 EI. 可见,U≠+ 但是,若构件上有两种载荷,其中的任一种载荷在另一种载荷所产生的位移上不做功 则该两种载荷作用下的变形能等于它们分别作用下的变形能之和,即可实行叠加·上面所讲 的组合变形时的变形能计算就属于这个情况。 例13-1简支梁跨中受集中力P的作用,求跨中的挠度,设抗弯刚度E:已知 A B 一⅓ 例13-1图 解:首先,计算梁的变形能,梁AC段任一横截面的弯矩是 运用对称性得变形能 分 PP 96EI. 239 This document is generated by trial version of Print2Flash(www.printflash.com)