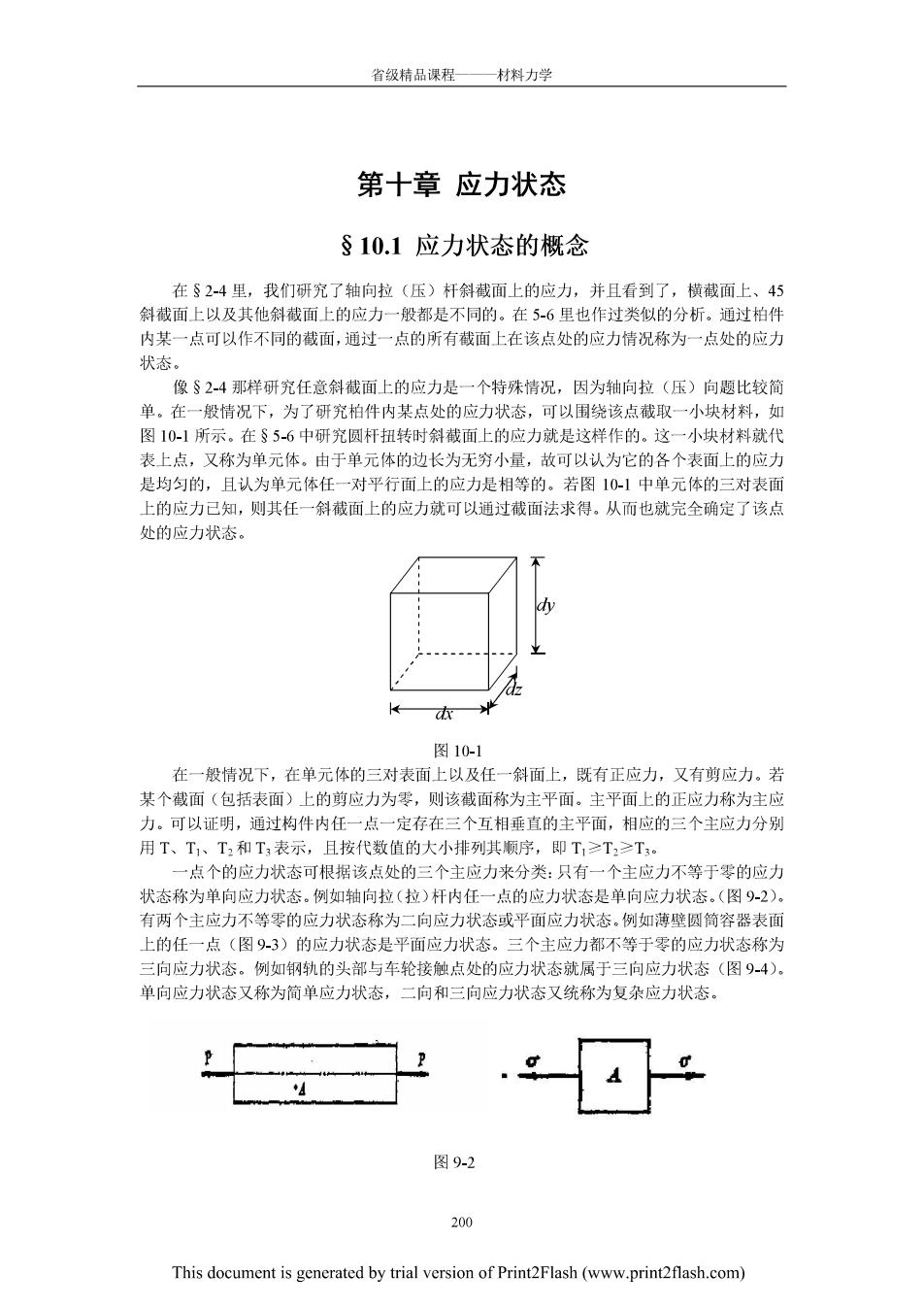
省领精品课程—材料力学 第十章应力状态 §10.1应力状态的概念 在S2-4里,我们研究了轴向拉(压)杆斜截面上的应力,并且看到了,横截面上、45 斜藏面上以及其他斜截面上的应力一般都是不同的。在5-6里也作过类似的分析。通过柏件 内某 一点可以作不同的截面,通过一点的所有截面上在该点处的应力情况称为一点处的应力 状态。 像§2-4那样研究任意斜截面上的应力是一个特殊情况,因为轴向拉(压)向趣比较简 单。在一般情况下,为了研究怕件内某点处的应力状态,可以围绕该点截取一小块材料,如 图10-1所示。在S5-6中研究圆杆扭转时斜截面上的应力就是这祥作的。这一小块材料就代 表上点,又称为单元体。由于单元体的边长为无穷小量,故可以认为它的各个表面上的应力 是均匀的,且认为单元体任一对平行面上的应力是相等的。若图101中单元体的三对表面 上的应力已知,则其任一斜截面上的应力就可以通过截面法求得,从而也就完全确定了该点 处的应力状态。 图10-1 在一般情况下,在单元体的三对表面上以及任一斜面上,既有正应力,又有剪应力。若 某个截面(包括表面)上的剪应力为零,则该截面称为主平面。主平面上的正应力称为主应 力。可以证明,通过构件内任一点一定存在三个互相垂直的主平面,相应的三个主应力分别 用T、T、2和T表示,且按代数值的大小排列其顺序,即T,≥T,≥T。 点个的应力状态可根据该点处的三个主应力来分类:只有一个主应力不等于零的应力 状态称为单向应力状态。例如轴向拉(拉)杆内任一点的应力状态是单向应力状态.(图92》 有两个主应力不等零的应力状态称为二向应力状态或平面应力状态。例如薄壁圆筒容器表面 上的任一点(图93)的应力状态是平面应力状态。三个主应力都不等于零的应力状态称为 三向应力状态。例如钢轨的头部与车轮接触点处的应力状态就属于三向应力状态(图94)。 单向应力状态又称为简单应力状态, 二向和三向应力状态又统称为复杂应力状态。 图9-2 200 This document is generated by trial version of PrintFlash(www.printflash.com)

省级精品课程 一材料力学 (4 图94 例10-1分析图9-3所示圆柱形薄壁容器表面上D,点的应力状态。 解:在第二章练习题2-33里己经求出容器横截面和纵截面上的正应力分别是 即(217)和(218)式。若在容器表面上取一点D,的上下一对表面上有T,左右一对表 面上有T。D2的前面是容器外表面,应力为零。又由于D,三对表面上剪应力为零,故该 三对(个)表面都是主平面,相应的正应力为主应力。按代数值的大小排列,D:的三个主 应力是 41 ,00 D2为平面应力状态。有时侯为了简化,只画出单元体的平面图,见图9-3。 201 This document is generated by trial version of PrintFlash(www.printflash.com)
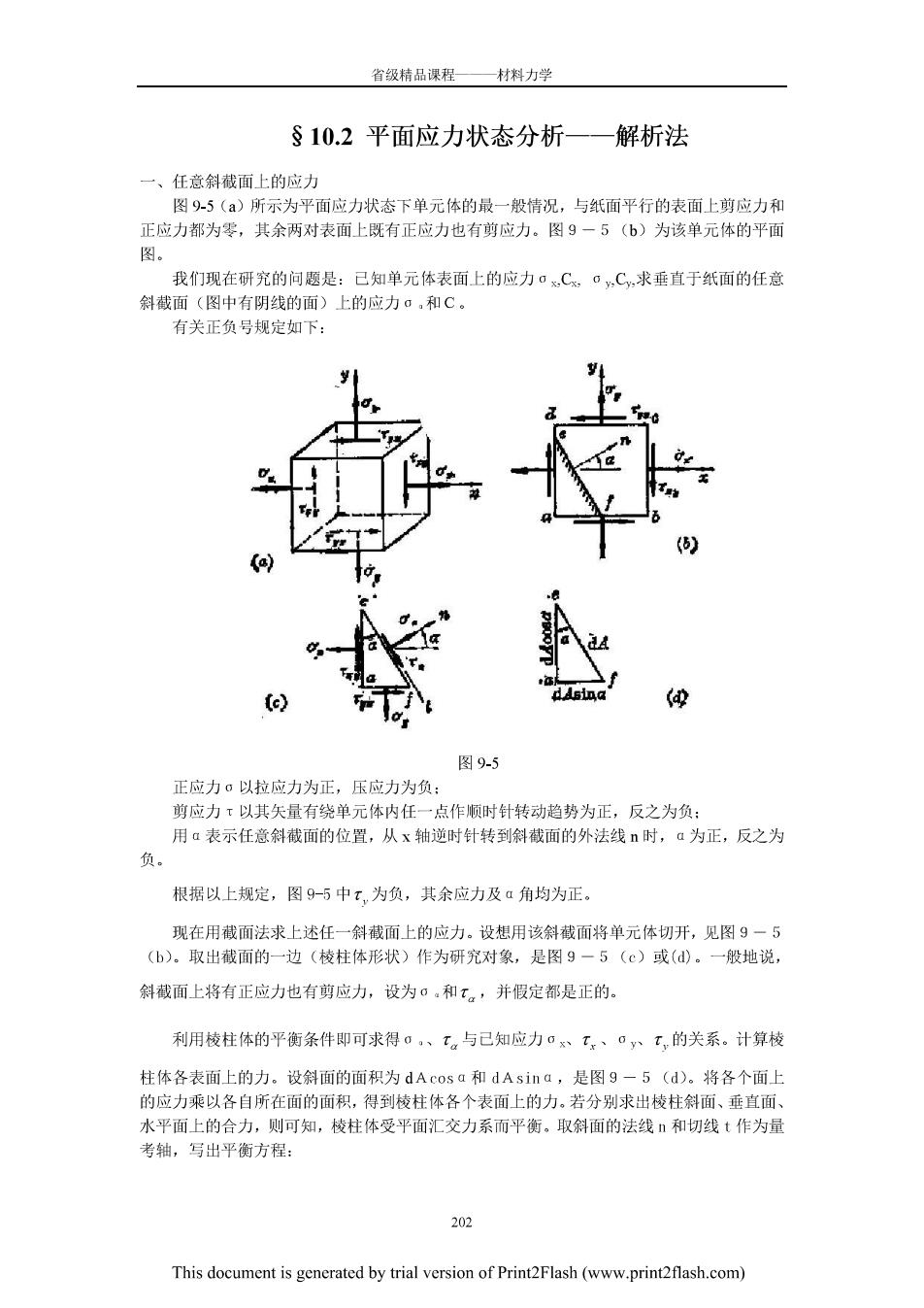
省领精品课程—材料力学 §10.2平面应力状态分析一一解析法 一、任意斜截面上的应力 图9-5(a 所示为 面应力状态下单元体的最一般情况,与纸面平行的表面上剪应力和 正应力都为零,其余两对表面上既有正应力也有剪应力,图9一5(6)为该单元体的平面 图。 我们现在研究的问题是:已知单元体表面上的应力o,C。·,C,求垂直于纸面的任意 斜裁面(图中有阴线的面)上的应力。,和C。 有关正负号规定如下 (c) 图9-5 正应力·以拉应力为正,压应力为负: 剪应力π以其矢量有绕单元体内任一点作顺时针转动趋势为正,反之为负: 用α表示任意斜截面的位置,从x轴逆时针转到斜截面的外法线n时,a为正,反之为 负 根据以上规定,图95中,为负,其余应力及a角均为正 现在用藏面法求上述任一斜截面上的应力。设想用该斜被面将单元体切开,见图9一5 (b).取出截面的一边(棱柱体形状)作为研究对象,是图9一5(c)或()。一般地说, 斜截面上将有正应力也有剪应力,设为。:和t。,并假定都是正的。 利用棱柱体的平衡条件即可求得。,、t与已知应力·xT,、·yT,的关系。计算棱 柱体各表面上的力。设斜面的面积为dAcos a和HAsina,是图9一5(d)。将各个面上 的应力乘以各自所在面的面积,得到棱柱体各个表面上的力,若分别求出棱柱斜面、垂直面 水平面上的合力,则可知,枝柱体受平面汇交力系而平衡。取斜面的法线n和切线t作为量 考轴,写出平衡方程 202 This document is generated by trial version of Print2Fash(www.printflash.com)

省领精品课程 一材料力学 odA-(o,dAcosa)cosa+(r,dAcosa)sina (a) -(a,disina)sina+(tdAsina)cosa=0 rdA-(o,dAcosa)sina-(,dAcosa)cosa +(o dAsina)cosa+(r,dAsina)sina=0 根据剪应力互等定理,.t,和x在数值上相等。由三角公式有cos2ā号(1+cos2a), m2a分(1-cos2a),2 in0sa=sin2a,代入以上两式,整理得 o。=7(o,+o,)+(cx-c,)cos2a-t,sin2a(10-l) t(-,)sin 2a+t,cos2a (10-2) 公式(10-1)和(10-2)表明,若已知单元体表面的应力,则任意斜截面上的应力0,和 t。可以求出:还可以看到,O。和t。是a的函数,即应力随截面位置而改变。 二、主应力和极值剪应力。 首先研究极值正应力。因为o,是α的函数,由数学分析,令 0,-0j水2ma)ecas2a)=0 (.-)sin 2a+t,cos2a=0 (e) 由此得到 tan 2d-, -2T (10-3) 因为tga=tg(180°+a),所以满足该式的a。值有两个:a和(a+90°).即极值正应力 1 有两个,它们所在的平面互相垂直。利用三角公式cos2ac +g2 。·cos2a。由(10-3)式求出cos2a。和sin2a,代入(10-1)式并注意到a=a。及a= a+90°,由此求得极值正应力的大小 (10-4) 再来求主应力。由定义,设α=Q。时代表主平面,则由(10-2)式有 ,)sin 2a,+r,cos2a=0 (d) 比较(c入(仙两式知,主平面也就是极值正应力所在的平面,因而主应力也就是极值正应 刀。 下面研究极值剪应力。由(102)式,令 203 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 ,)(2co 2a)+1,-2si2a) tan 2a =.- (10-5) 满足(10-5)式的a:值也有两个:a1和a+90°,对应于这两个极值位置,由(10-2)式求 得两个极值剪应力分别为 (10-6) 比较(10-4)和(106)式,得到极值剪应力和主应力的关系: (10-7) 比较(10-3)和(10-5)式,由于 tg20,tg20=-1 可知极作煎应力所在的平面与主平面的夹角为45” 极值蓟应力所在的平面上的正应力通常不为零,将a:和a+9心分别代入(10-1)式, 并用表示这个正应力,得 0,之(o+a分(0 d (10-8) 例10-2矩形截面简支梁如图(a)所示,试从D点处取出单元体。 204 This document is generated by trial version of Print2Flash(www.print2flash.com)