
省级精品课程—材料力学 由以上三式可以看到,P。、。、t均为α的函数,也就是说,不同的截面 上应力不同。最大应力对我们很有用 当a=0时,6s=g,t。=0 即最大正应力发生在横截面上,O=。,该截面上的剪应力为零。 当a=45时,lrm=20,a。= 即最大剪应力发生在与轴线成45°的斜面,?=20,该斜面上的正应力也 等于横截而上的正应力的一半。 §2.5轴向拉(压)杆的强度计算 首先建立两个概念:工作应力和容许应力。构件在载荷作用下产生的应力称 为工作应力。实际工程中,为了保证构件能正常地工作,即不发生破坏,对不同 材料的各类构件的工作应力都规定了一个容许的值,称为这材料的容许应力。容 许应力是在实验的基础上规定的。容许正应力记为[。]。 这样,构件能正常工作,即不发生破坏的条件是:构件内最大工作应力不得 超过材料的容许应力。对于拉(压)杆这个条件是: A ≤ (2-9) (2-9)式称为拉(压)杆的强度条件 应用强度条件(29》 可以解决以下三类强度计算问题 1.强度校核已知杆的尺寸、载荷以及材料的容许应力,验算杆件是否满 足强度要求。 2.设计截面已知载荷及材料的容许应力,确定杆的最小横截面积。即 3.确定容许载荷已知杆的横截面积和材料的容许应力,确定容许载荷。 即 Ns≤[o]A 例2-3:有一高度1=24m的方形截面等直石柱,截面边长为1.5m,其顶部受轴 向载荷P-1000KN作用,见图2-9(a)。已知材料的容重Y=23KN/m,容许应力 [o]=1MPa,试校核石柱的强度。 解:首先计算石柱的轴力,图2-9(b)就是分离体,由分离体的平衡条件 得。 N=-(P+YAx)(压力) This document is generated by trial version of Print2Flash(www.print2flash.com)
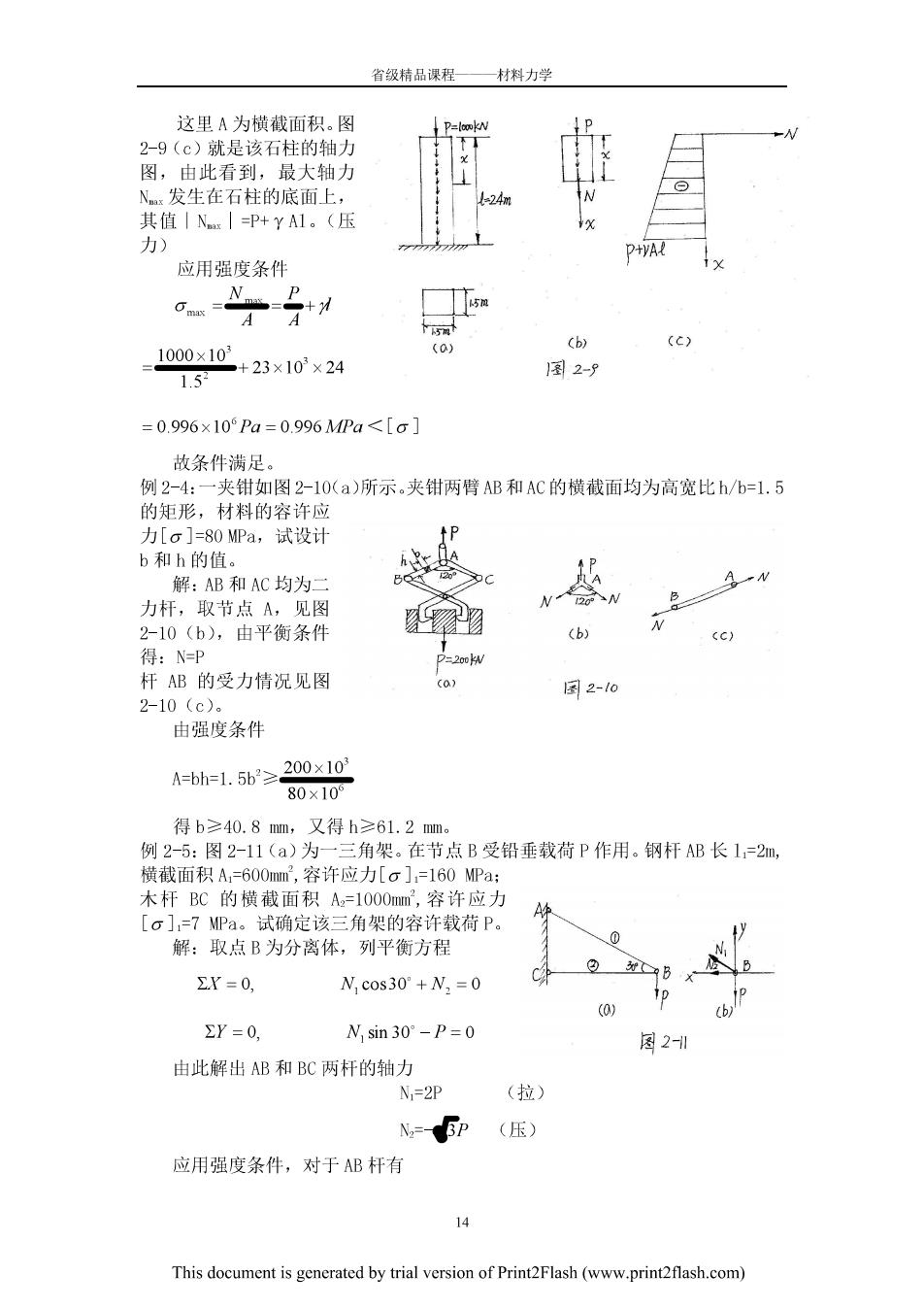
省领精品课程 一材料力学 这里A为横截面积。图 2-9(c)就是该石柱的轴力 图,由此看到, 最大轴力 发生在石柱的底面上, 其值|N|=P+YA1。(压 力) 应用强度条件 1000×10+23×103×24 (b) 1图2-9 152 =0.996×10Pa=0.996MPa<[c] 故条件满足。 例2-4:一夹钳如图2-l0(a)所示.夹钳两臂AB和AC的横截面均为高宽比h/b=1.5 的矩形,材料的容许应 力[g]=80MPa,试设计 b和h的值。 解:AB和AC均为 一水 力杆,取节点A,见图 B 2-10(b),由平衡条件 (b) (c) 得:N=P 杆AB的受力情况见图 o 国2-10 2-10(c》 由强度条件 A=bh=1.5b≥200x10 80×10° 得b≥40.8m,又得h≥61.2m 例2-5:图2-11(a)为 角架 。在节点B受铅垂载荷P作用。钢杆AB长1,=2m 横截面积A:=600mm,容许应力[c]=l60MPa: 木杆BC的横截面积A=1000mm’,容许应力 [o]=7MPa。试确定该三角架的容许载荷P。 解:取点B为分离体,列平衡方程 =0, B Ncos30°+V=0 (0) p 6 Y=0, N1sin30°-P=0 图21 由此解出AB和BC两杆的轴力 N,=2P (拉》 N=3p (压) 应用强度条件,对于AB杆有 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 有600x10≤160X10 2P 所以P≤48×103N 对于BC杆有 BP 700x10≤7X10 所以P≤40.4X10N 故三角架的容许截荷可取P=40.4KN。 §2.6应力均匀分布的适用条件、应力集中的概念 一、圣维南原理 工程实际问题里,外力可以通过各种方式作用于杆上。图2-12所示为同样 的拉杆,上端的受力方式不同,但这些力都是静力等效的。圣维原理指出,力作 用于杆端方式的不同,只会使与杆端距离不大于杆的横向尺寸范围内的应力受到 影响。在图2-12中,只在图示虚线范围内也就是在力作用的局部,各杆的应力 分布不同, 在离开杆端局部范围之外,应力都是 ,而按(2-5 ) 计算横批 面上的正应力,应力均匀 分布,而可以不考虑力的作 用方式。 p 圆2-2 二、应力集中的概念 根据实际需要,右要在构件上钻相,开抽等,文就引起件错截面尺十的 突然改变。这样的杆在轴向拉(压)时,在截面突然变化的部位横截面上的正应 力不再均匀分布,应力局部增大,而离开该部位稍远的地方应力又趋于均匀。这 种由于截面尺寸突然改变而引起应力局部增大的现象称为应力集中,见图2-13 (a)、(b)、(c),应力集中的程度有理论应力集中系数,表示: = (2-10) 式中σ为1-1截面上的最大应力,σ为该截面上的平均应力。构件在拉压、 公 This document is generated by trial version of Print2Flash(www.print2flash.com)
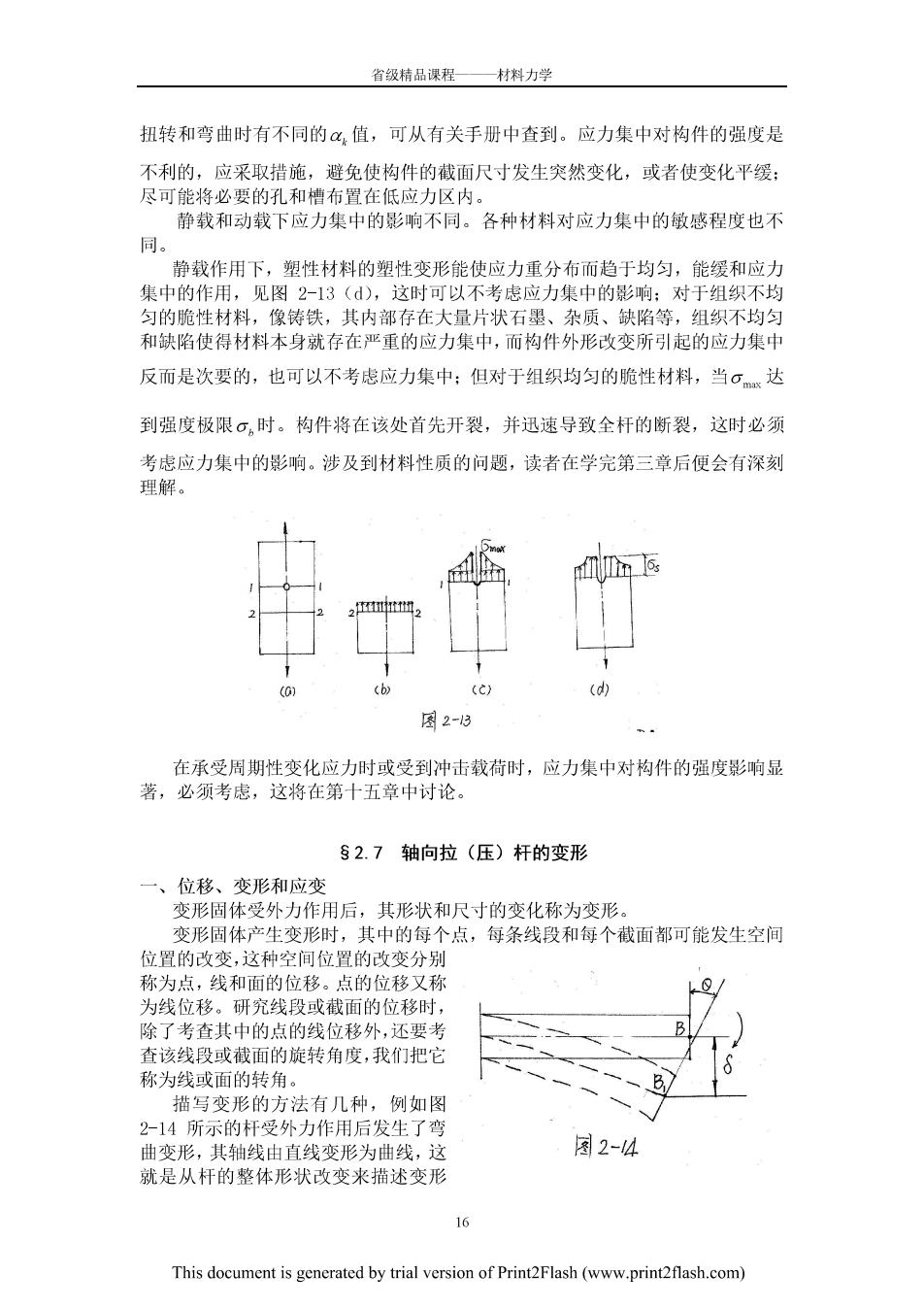
省级精品课程 材料力学 扭转和弯曲时有不同的x,值,可从有关手册中查到。应力集中对构件的强度是 不利的,应采取措施,避免使构件的截面尺寸发生突然变化,或者使变化平缓 尽可能将必要的孔和槽布置 低应力区内 静载和动载下应力集中的影响不同。各种材料对应力集中的敏感程度也不 同。 静载作用下,塑性材料的塑性变形能使应力重分布而趋于均匀,能缓和应力 住中的作用,见图2-13(d).这计可可以不考虑应力典中的号影响:对干组织不均 匀的脆性材料,像铸铁,其内部存在大量片状石墨、杂质、缺陷等,组织不均匀 和缺陷使得材料本身就存在严重的应力集中,而构件外形改变所引起的应力集中 反而是次要的,也可以不考虑应力集中:但对于组织均匀的脆性材料,当。达 到强度极限。,时。构件将在该处首先开裂,并迅速导致全杆的断裂,这时必须 考虑应力集中的影响。涉及到材料性质的问题,读者在学完第三章后便会有深刻 理解。 ( 图2-3 在承受周期性变化应力时或受到冲击载荷时,应力集中对构件的强度影响显 著,必须考虑,这将在第十五章中讨论。 §2.7轴向拉(压)杆的变形 一、位移、变形和应变 变形固体受外力作用后,其形状和尺寸的变化称为变形。 变形固体产生变形时,其中的每个点,每条线段和每个截面都可能发生空间 位程的改变,这种空间位程的改变分别 称为点,线和面的位移。 点的位移又称 为线位移。研究线段或截面的位移时 除了考查其中的点的线位移外,还要考 查该线段或截面的旋转角度,我们把它 称为线或面的转角。 描写变形的方法有几种,例如图 2-14所示的杆受外力作用后发生了弯 曲变形,其轴线由直线变形为曲线,这 园2-4 就是从杆的整体形状改变来描述变形 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 的,§1-2所讲的杆的基本变形式就是这样 1 》折的。其实,若给出B载面的转角日和卫 截面形心的垂直位移6,则图2-14所示杆 95ta5 D16 的弯曲变化也就得到控制,利用控制点的位 038 来描写杆的变形也是一种方法。还有一种方 (b) 法,如果将构件的任意局部变形弄清楚了, (0) 则整个构件的变形也就解决了。局部变形的 图2-5 描写方法是对于构件内任意 占0.首先 0占的任意微线段的伸长或缩短的程度,如图2-15(a)所示,设线段0B 变形的后的位置是OB1,伸长量是△S,则称 oB=im、 (2-11) 为0点沿0B方向的线应变,它表示了0点沿B方向的相对伸长或缩短。其次 再研究过0点的任意直角的改变。如图2-15(b)所示,设直角∠CD变形后为 ∠C,0D,则 Ya=lim((oD-∠CO,D) (2-12) 称为0点在C0D平面上的角应变。有了线应变和角应变,我们总可以把一点附近 的局部变形完全表示清楚,至于如何表示我们将根据具体问题逐步学习。 二、拉(压)杆的纵向变形 由验得到拉(压)轩的纵向您形规独,拉伸时纵向伸长,压缩村纵向培短 当材料不超过弹性范围内时,其伸长或缩短量△与轴力N和杆长1成正比,与 横截面积A成反比,即 4/=M (2-13) FA 式中E为比例常数,称为材料的弹性模量,是一个材料常数。由(2-13)式看到,EA 越大则△W越小,EA称为拉(压)杆的刚度 纵接移4山=- 横向镀彩4d=dd -16 因为。=N1A,拉(压)杆的变形是均匀的,故任一点的纵向应变可用平 均值表示,即ε=△1,代入(2-13)式并路去下标得到 6=或o=EE (2-14) 我们把(2-13)和(2-14)式都称为虎克定律,它们是两种不同形式,前者 表示杆的总伸长或缩短量与轴力之关系,后者表示任一点附近的应变和应力之关 系。 三、拉(压)杆的横向变形 This document is generated by trial version of Print2Flash(www.print2flash.com)