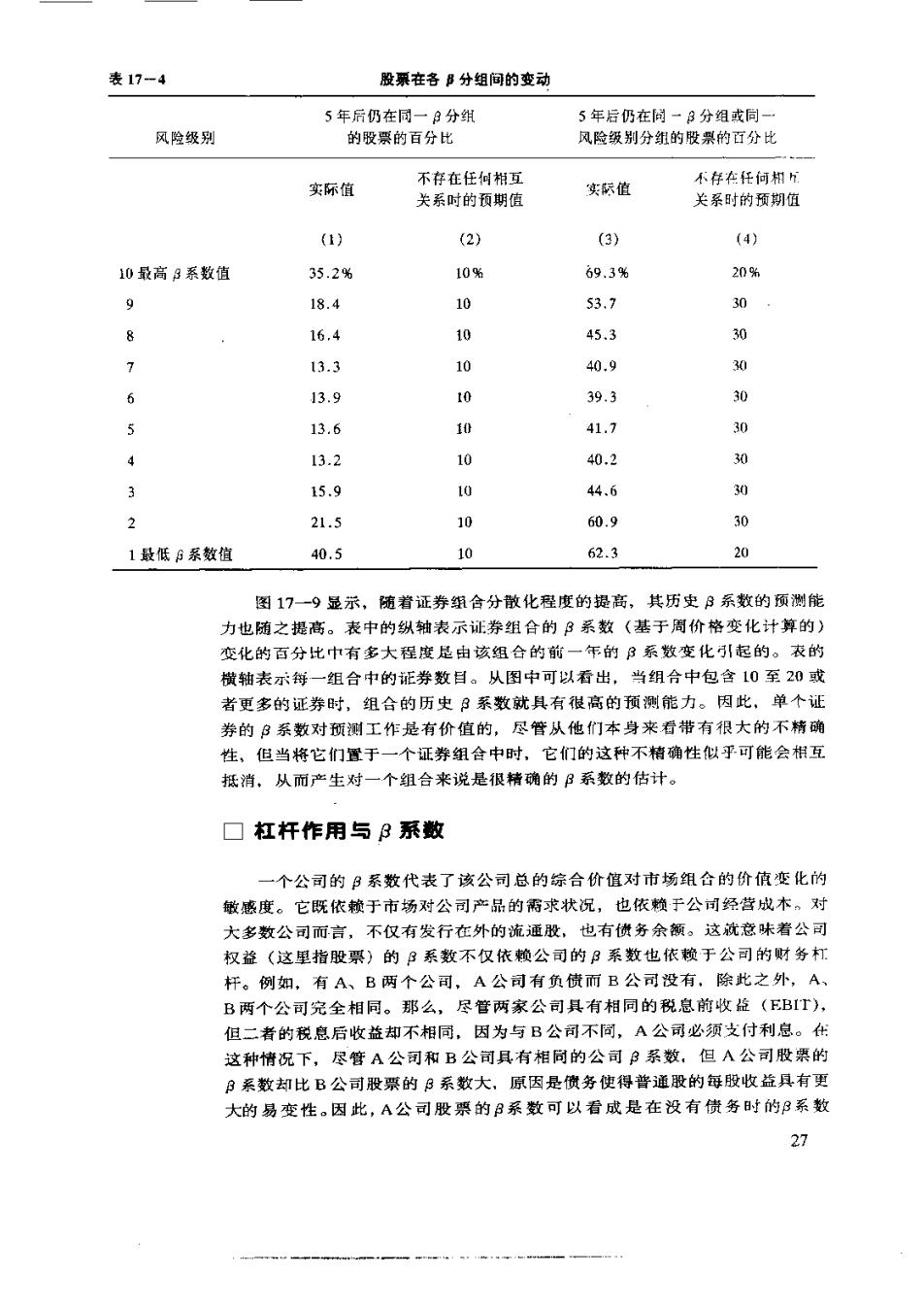
表17-4 股票在各B分组间的变动 5年后仍在同一日分组 5年后仍在同一B分组或同一 风险级别 的股票的百分比 风险级别分组的股票的百分比 不存在任何相h 实际值 不存在任何相互 关系时的预期值 实际值 关系时的预期值 () (2) (3) (4) 0最高3系数值 35.2% 10% 69.3% 20% 9 18.4 10 53.7 30 8 16,4 10 45.3 30 7 13.3 10 40.9 30 6 13.9 10 39.3 30 5 13.6 0 41.7 30 4 13.2 10 40.2 30 15.9 公 44.6 30 21.5 10 60.9 30 1最低B系数植 40.5 10 62.3 20 图17一9显示,随着证券组合分散化程度的提高,其历史B系数的预测能 力地随之提高。表中的纵轴表示证券组合的3系数(基于周价格变化计算的)》 变化的百分比中有多大程度是由该组合的前一年的3系数变化引起的。衣的 横轴表示每一组合中的证券数目。从图中可以看出,当组合中包含10至20或 者更多的证券时,组合的历史B系数就具有很高的预测能力。因此,单个证 券的B系数对预测工作是有价值的,尽管从他们本身来看带有很大的不精确 性,但当将它们置于一个证券组合中时,它们的这种不精确性似乎可能会相互 抵消,从而产生对一个组合来说是很精确的B系数的估计。 口杠杆作用与3系数 一个公司的B系数代表了该公司总的综合价值对市场组合的价值变化的 敏感度。它既依赖于市场对公司产品的需求状况,也依赖于公司经营城木。对 大多数公司而言,不仅有发行在外的流通股,也有债务余额。这就意味着公司 权益(这里指股票)的B系数不仅依赖公司的系数也依赖于公司的财务杠 杆。例如,有A、B两个公司,A公司有负债而B公司没有,除此之外,A、 B两个公司完全相同。那么,尽管两家公司具有相同的税息前收益(EBIT), 但二者的税息后收益却不相同,因为与B公司不同,A公司必须支付利总。在 这种情况下,尽管A公司和B公司具有相同的公司系数,但A公司股栗的 P系数却比B公司股票的B系数大,原因是债务使得普通股的每股收益具有更 大的易变性。因此,A公司股票的B系数可以看成是在没有债务时的B系数 27

100 变化百分比 50 10 汤 30 40 50 每…证券组合的证券数门 图17一9前一年的B系数变化引起的B系数值变化的百分比 (B公司股票的系数)加上·个公司债务余额后的调整数。 人们已经找到·种方法来衡量债务对公司股票B系数的彩响,该方法包 括四个处理步骤: 第一,决定(计算)公司目前债务余额的市值(D)和股票的市值(E), 这样,具有财务杠杆的公司的市场价值(V)可由下列公式表示: VL=D+E (17.10) 第一二,不含财务杠杆作用的公司的市场价值也应被确定下来,我们可用下 列公式表示: V.=VL-TD (17.11) 其中:V。=没有杠杆作用的公司的市场价值; T=平均的公司所得税税率: D=公司债务余额的市场价值。 第三,通过估算公司债务的B系数Ba,和公司股票的B系数Bv,可以求 出公司的B系数,计算公式如下: n=RhxL-》D+R是 V。 (17.12) 第四,用公式(17.12)估算了公司B系数之后,杠杆作用对公司股票的 影响程度就通过公式(17.12)的变形公式求得。从方程(17.12)中求出 Ba,结果如下: R=n+(Pn-Rh)(号)1-T) (17.13) 在公式(17,13)中应该注意,当公司的偾务权益比率D/E发生变化时, 公司B系数Bm并不会改变。当假设偾务B系数B做不变,则提高公司的馈务 一一权益比率就能增加公司股票的值。从直观上来说,这种关系其有一定的 经济意义,因为提高公司债务一资本比例会使公司的税后收益具有更大的易变 性。相反,降低公司的债务一资本比例,就能使税后收益的易变性减少,从而 降低其股票的B值。 当公司最近改变了债务一资本比例(或正准备增加这-一比例)时,B系数 28

的这一属性对预测公同股票的B系数1十分有用。例如,对ABC公司,直到上 个刀以前,公司总资严为1亿美元,其中资本余额为6000月美元,债务余额 为4000万美元,税率为30%。用表17一2中所述的特征线模型对公司上个月 以前的数据进行计算。则公司股票(或资本)利和债务的系数分别为1.40和 0.20。现在,ABC公司又发行了2000万美元的股票,并用经营利润偿还了部分 债务。结果,ABC公司月前的资本余额和债务余额分别为7400万美元和2000 万美元(其,7400万美元的资本余额等于新发行的2000万美元股票加上原 来的6000万美元资木余额减去6000万美元税牧;2000万美元的债务余额是原 米的货务余额减去公司所偿还的部分求出的)。ABC公司股票的B系数在进行 这种资本结构调整后会是多少呢? 该问题可以用前面所介绍的方法米回答。首先,利用公式(17.10)可知 在新股发行以前公司价值为1亿美心:第二,从公式(17.11)可计算出不包含 杠杆作用的公司价值为8800万美元(一1亿美元-0.3×4000万美元);第三, 公司的3系数可用公式(17.12)作如下计算: A-0.20×[1=08992i类正]+1.40×台868羹2=1.02 8800方美元 最所,当前的公股票系数(即发行2000万美元新股以后的股票日系数) 可州公式(17.13)计算出来: Rn-1.02+1.02-0.20)×号98男装2×(1-0.30)=1.17 因此,从上面的计算可以肴出,当减少ABC公司的债务余额时,其股票的B 系数也从1.40降到了1.17。 ☐行业B系数 处于较高周期性需求和具有较人固定成本的企业,比之处于具有较为稳定 的需求利和较大可变成木的企业,~般说来可以衡期其具有更高的B系数,因 为前者的税息前收流其有更大的可变性。人们可能会设想,财务杠杆的作用可 能光全消除上述因素的影响,使不同行业中企业的股票B系数趋于基本相同。 然而,事实并非如此,某些行业的公同确实倾向于比另“些行业的公司具有更 高的股票分系数,而且从总的情况来看,其分类与前面的预期基本一致。 表17一5显示了不同的行业分类中公司股票B系数的平均值。对于那些生 产“必需品”的公司来说,当人们对经济前最的预期发生改变时,与其他大多 数公司相比,其股票价格会作出较小反应。即这类生产必需品的公司(如公用 事业或食品行业)更倾向于有较小的B值,因为它们有更稳定的收益。相反, 对于那些生产“奢侈品”的公司来说,当人们对经济前景的预期发生改变时, 与其他大多数公司相比,其股票价值会作出较大的反应。即这类生产著侈品的 公司(如旅游服务和电器生产行业)更倾向护有较大的B值,因为收益更具 周期波动性。 B系数的预测表17一5中所提供的数据可以用来调整历史B系数。例 如,若知道某个公司是航空运输企业,则可以有理由假定其股票的先验的 系数为1.8,因此,将其股栗的历史B系数向1.8调整就比用公式(17.9)向 29

所有般票的平均值1.0调整更为合理。 表17-5 部分产业股票系数的平均值,1966一1974年 产业名称 B系数值 产业名称 3系数值 空中运输 1.80 能源、原材料 1.22 房地产 1.70 轮胎、橡胶制品 1.2 旅游、户外消遭 1.66 公路、海运 1.19 电子 1.60 木制品、纸业 1.16 各种金融 1.60 联合企业 1.14 非耐用品、娱乐业 1.47 药品业 1.14 耐用消费品 1.44 国内石油业 1.12 商业机器 1.43 肥皂、化妆品 1.09 零售、批发 1.43 炼钢 1.02 新闻媒介 1.39 集装箱 1.01 保险 1.34 有色金减 0.99 货物运输 1.31 农业、食品 0.99 小商品生产 1.30 酒业 0.89 航天 1.30 国际石油 0.85 商业眼务 1.28 银行业 0.81 服装 1.27 烟草业 0.80 建筑业 1.27 电话通讯业 0.75 机动车 1.27 公用事业 0.60 胶片、光学仪器 1.24 黄金业 0.36 化工 1.22 对历史系数的调整方法实际上包含了对未来?系数的预测公式。公式 (17.9)可以更一般地表示为: B。=a+b娲 (17.14) 其中,a,b是常数。如果考虑到不同行业日系数的区别,可将公式(17.14) 改写为: B。=a明d+bp (17.15) 其中日,表示该行业的公司股票的B系数的平均值。 例如,设a和b的取值分别为0.33和0.67,空中特快是…个航空运输业 的公可,其历史系数为2.0,周整B系数是多少呢?若注意到航运输业股 票的3系数为1.8,则空中特快般票的调整B系数就可以用公式(17,15)计 算出来: 月。=(0.33×1,8)+(0.67×2.0)=1.93 因此,空中特快的调整B系数为1.93,介于其历史B系数2.0利行业P系数 1.8之间。事实上,这就是公式(17.15)所要达到的目的,将历史3系数调 整为历史B系数BA和行业B系数B的一个中间值。 30

跨行业的公司对于跨行业经营的公司义如何处理呢?如果一个公司同 时经营两个行业,则公式(17.15)可改写为: 月.=a(Ed1×Baal+Ein2×3nu2)+bpa (17.16) 其中,Ed1和Ea2分别表术公可在行业1和行业2中的收益比重,只,和B2 分别为这两个行业的B系数 例如,对电望远镜公司,其一半的收益来自电器行业,分·半的收益来 自于航天工业,假设a和b分别为0.33和0.67,而该公司的仍史3系数为 1.2,则调整的B系数可分下列两步计算: 第-·,计算E1×3d1tE2×B2的值。运用表17-一5和上述假设数据. 可知该值为1.45(=0.5×1.6+0.5×1.3)。该数可以看作为任何在这两个行 业中经营且有大致相同的收益水平的公词的平均3系数: 第.二,用公式(17.16)将电子望远镜公可的历史系数调整为1.28(= 0.33×1.45+0.67×1.20)。注意,该值介于其历史3系数1.20和它所处的 “行业”B系数1.45之间。 居于财务特征的调盛 各种有关的金融财务信息也可以川于调整公可的 3系数。比如,具有较高股息发放率的股票可能具有较小的3系数,因为其价值 是与近期股息而不是远期股息相联系。相应地,公式(17,16)可作如下修正: 月。=a(Ea1×Baul+Fmd2×Bu2)+b3+cY (17,17) 其中,c是常数,Y是公股票的股息率。 表17一6所示的就是这种形式的-个预测公式,它所用的是1982年间可的 历史数据。用这种公式来预测-一种证券的B系数,首先确定该证券所属行业 或部门的常数,然后用该常数上该证券的历史日系数乘以0.576(注意,这 与用公式(7.9)对历史B系数作调整是类似的),最后,再加上:(1》证券 的股息收益率乘以-0.019;(2)证券的“规模属性”乘以-0.105。用代数形 式表示出来,模型为: B。=a,+(0.576×a)+(-0.019×Y)+(-0.105×S)(17.18) 其中,4,为证券所属行业的常数、民为证券的历史B系数,Y为股总种,S 是公司的规模。根据这一公式,如果一种证券具有较高的股息收益,或较大的 股票(资本)余额市场价值,则可以预测其将具有较小的B系数。 应用举例设一种股票被划为碱于“基础产业”的行业,历史系数 为1.2,过去12个月的股息收益率为4%,资本余额的总市值为70亿美元 (即公司有1亿股在外流通股,每股市价为70美元)。运用公式(17.18),则 调整3系数为: 3。=0.455+(0.576×1.2)+(-0.019×4)+L-0.105×Log7] =0.455+0.69-0.08-0.09 =0.98 这种基于多因素模型的预测公式与那柴仅仅适用历史3系数的预测公式 相比,与历史数据更加吻合。根据-一项研究报告,它的准确性比其他简单的B 系数调整方法提高了86%。然而,该数字仅仅表明对某一组给定数据而言的 预测精度。对于一个预测公式的真正检验,在于其“预测”的能力,而这 点,只有在最后的实际分析中,通过使用这些方法的大量的经验才能得出对各 31 ”一””卡