
续前表 (B)计算 19系数 (T×8XY)-(y×SK)-16×590.80)二(54.84×66:622=0.63 (T×∑X2)-(∑X)2 (16×848.38)-(66.62)2 2.a系数: (2Y/T)-[月×(2X/T)}=[54.84/16]-[.63×(66.62/16)月=0.79% 3.随机误差项标准离差: ↑【Y2-Alpha×Y)-(3×XY)】/[T-2]fn =}【1039.03-(0.79×54.84)-(0.63×590.80)]/[16-2]}2=6.67% 4.系数的标准差: 随机误差项标准离差/1∑x2-[〈∑X)2/T] =6.67/1848.38-[(66.62)2116]112=0.28 5.a系数的标准差: 随机误差项标准离差/1T-L(X)2/∑X]}2 =6.67/116-[(66.62)2/848.38:12=2.03 6.相关系数: 公(x-x》(y-) n∑xy-Σx·∑y 分r-.2y-n2-四227 (T×公XY)-(Y×2X) :L(T×ΣY2)-(ΣY)21×[(T×x2)-(Σx)2]西 (16×590.80)-(54.84×66.62) 11(16×1039.03)054.84月×(16×849.38)-(66.62P]m=0.52 7.决定系数: (决定系数)2=(0.52)2=0.27 8.非决定系数: 1-决定系数=1-0.27=0.73 同理,最佳拟合直线一定具有最小的随机误差平方和,也就是说,与问 直线相对的16个随机误差的平方和将比其他任一直线求!的随机误差平方和 要小。 例如,在公式(17.8)中,如果a等于1.5%,B等少0.8,则就可以将 16个季度的随机误差项ewM求出,将这16个数的平方和除以14(=16一2), 耳求平方和,就可以算出随机误差项的标准离差。然而,这一标准离差将大于 以a等于0.79%和月等于0.63作:的最佳拟合直线所求出的随机误差项的标 准离差—6.67%。 需要记住的-一点是,一种证券的“真实的”历史B系数是不能被观察到 的,所能做的只是计算其估计值。因此,即使-一种证券的“真实的”系数永 远保持不变,我们用表17一2中的方法求出的B系数的估计值也会经常变化, 因为估算中存在各种各样的误差(即选择误差)。例如,如果以另外16个季度 22

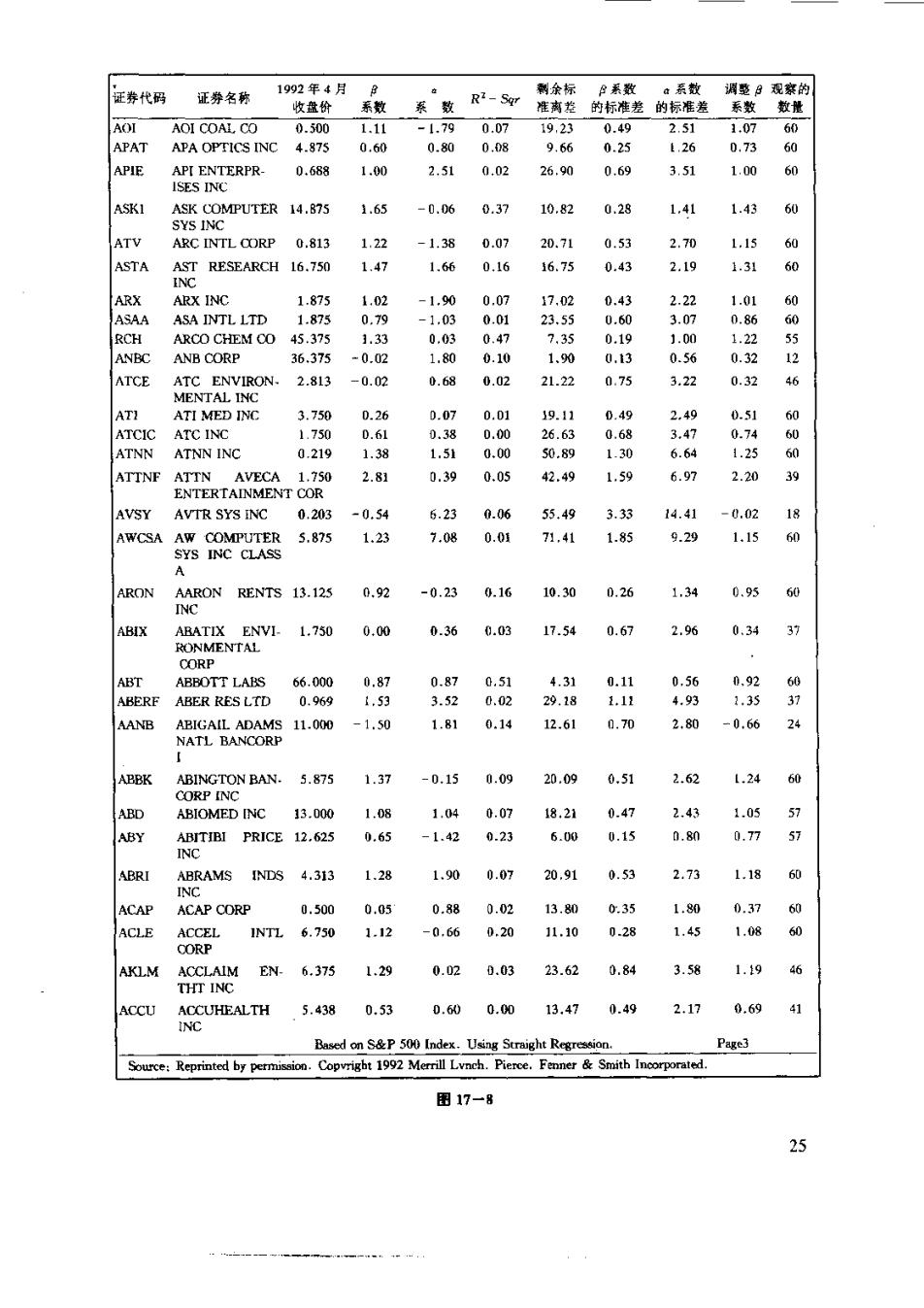
g ★ 第14季度 0% ★ ★★★ ★★ ★ 5.08% ★ ★ 10% 5% ★5% 10% ★ 10% 雷17一7怀杰特制造公司的市场横型 的数据作样本来计算,刚求出的怀杰特的估计B值几乎肯定会与用表17一2中 的数据算出的0.63不同。表17一2中所列的B的标误差《stand8 rd error of bea》表示这种枯计的误差穆度。在给定一系列必要假设的条件下(比如, “真实的”B在此16个季度内不发生变化),“真实的”B值有2/3的机会是落 在B估计值的加、减…个标准误差的粒图内。因此,可以说怀杰特的“真实 的”B值很可能大于0.35(=0.63-0.28)且小于0.91(=0.63+0.28)。类 似地,a的标准误差(standard error of alpha)地表示了在a估计值计算中选择 误差的大小。 表17一2中对出的相关素数(correlation coefficient)代栽了杯杰特的牧益 率与市场指数收益率之间相关的紧密程度。由于其取值范圈在+【与一】之间, 怀杰特的相关系数为0.52,说明二者之间只有适度的(或中等的)正相关关 系,即,当市场指数的收益率越大时怀杰特的收益率也越大。 决定系数(coefficient of determination)表示怀杰特收益率的变化中有多 大比例与市场指数收益率的变化有关,即,怀杰特收益率的变动中在多大程度 上可用市场指数的变动来解释。怀杰特的决定系数为0.27,就表示在这16个 季度的估算期间中,怀杰特的收益率的变动有27%的部分是由于市场指数牧 益率的变动引起的。 由于非决定系数(coefficient of nondetermination】等于1减去决定系数, 它就表示了怀杰特收益率的变动中有多大程度不是由于市场指数运动引起的。 怀杰特的非决定系数为0.73,说明其收益率的变动中有73%的部分与市场指 数运动无关。 图17-一8摘自美林公间(Merill Lynch)的《证券风险评估》报告。其中 是用表17一2中所述的计算方法对表中股票的价格变化百分比与标准·普尔 500指数的价格变化百分比在60个月中(不能获得足够数据的除外),逐月比 较,计算出?个对股票分析有价值的指标。 表中项和。项下的数据分别表示了证券特纸线的斜率和截距,该直线是 该种股票与指数散点图的最体拟合直线。例如,在研究的60个月期间,ASK 23

计算机公司的股票的3值和a值分别为1.65和-0.06%。 表中R一Sqr(R平方的简称)项下的数据就是表17一2中所说的决定系 数。ASK股票的决定系数为0.37,说明ASK股票价格的变化中有37%的部 分在此60个月中是由市场指数变化的。 表中剩余标准离差的值就是表17一2中所说的随机误差项的标准离差。从 图17一8可知,ASK股票的剩余标准离差为10.82%。 表中贝塔系数的标准差表示B值的标准误差。ASK股票的该值为0.28, 说明ASK股票的“真实的”B值有2/3的可能性落在1,37(=1.650.28) 和1.93(=1,65+0.28)之间;同理,可以推断ASK股票的“真实的”a俏 有2/3的可能会落在~1.47(=-0.06-1.41)和1.35(=-0.06+1.41) 之间。 图17一8中第7个数据称为调整贝塔系数(adjusted beta),该数有特别的 意义,下面详细讨论。 口调整系数 在没有任何信息的前提下,我们有理由将一种股票的P系数估算为1,即 B系数的平均值。但是,如果有条件能观察到在某一期间该股票如何随市场指 数而变化,则对这种先验的估计值作出调整就是合理的。这种周整能产生个 更切合实际的的最后估计值,它处于1.0和最初的完全基于历史价格变化所 计算的B的估计值之间。 大多数计算阝系数的投资公司在作这种调整时都采用了较为固定的程序。 当然,它们也常常,甚至对不同的股票,作出某些特殊的调整。图7一8中的 调整B系数是用约34%的权数乘以市场的平均B值1.0再加上约66%的权数 乘以每一只股票的历史B系数的估计值而获得的。如ASK股票的调整B系数 为1.43(=0.34×1.0+0.66×1.65)。更一般的计算公式为: B。=(0.34×1.0)+(0.66×Bn) (17.9) 其中,B。和B.分别是调整B系数和历史系数。从公式(17,9)不难看出, 该公式采取了将一种证券的历史系数调整为更接近1.0的策略。对小于1.0 的历史B系数,调整后变得更大一些,但仍小于1.0,对大于1.0的历史系 数,经调整后变得小一些,俱仍大于1,0。之所以有这样的调肇结果,是因为 权数(这里指0.66和0.34)都为正且和数为1.0,因此,这种调整程序实际 是一种平均技术。 表17一3显示这一调整程序使历史日系数与未来B系数产生多大程度的差 别。表中第2栏是8种证券组合的未调整的历史系数(每-~种证券组合中都 包含100种股票),它们是基于1947年7月至1954年6月间的月价格变化求 出的(注意,这里特意选择了这一期间B值较大的证券组合作为样本)。表中 第3栏是用美林公司的方法计算的调整系数,表中第4栏是基于随后7年的 价格变化计算的。从表中不难看出,对大多数证券组合,已调整的B系数比 未调整的B系数更接近于相连的历史阝系数。这-一现象说明调整的历史B系数 比未调整的历史B系数能更精确地对未来β系数作出预测。 24 w。”心一·,小
证券代码 1992年4月 a系数 调整日观察的 证券名称 a R7-Sqr 剩余标P系数 收盘价 系数 系数 准南差的标准差的标准差 系数数量 AOI AOI COAL CO 0.500 1.11 -1.79 0.07 19,23 0.49 2.51 1.07 60 APAT APA OPTICS INC 4.875 0.60 0.80 0.D8 9.66 0.25 t.26 0.73 60 APIE API ENTERPR- 0.688 1.00 2.51 0.02 26.90 0.69 3.51 1.00 60 ISES INC ASKI ASK COMPUTER 14.875 i.65 -0.06 0.37 10.82 0.28 1.41 1.43 60 SYS INC ATV ARC INTL CORP 0.813 1.22 -1.38 0.07 20.71 0.53 2.70 1.15 60 ASTA AST RESEARCH 16.750 1.47 1.66 0.16 16.75 0.43 2.19 1.31 60 INC ARX ARX INC 1.875 1.02 -1.90 0.07 17.02 0.43 2.22 1.01 60 ASAA ASA INTL LTD 1.875 0.79 -1.03 0.01 23.55 0.60 3.07 0.86 60 RCH ARCO CHEM CO 45.375 1.33 0.03 0.47 7.35 0.19 1.00 1.22 55 ANBC ANB CORP 36.375 -0.02 1.80 0.10 1.90 0.13 0.56 0.32 2 ATCE ATC ENVIRON. 2.813 -0.02 0.68 0.02 21.22 0.75 3.22 0.32 46 MENTAL INC ATI ATI MED INC 3.750 0.26 0.07 0.01 19.11 D.49 2.49 0.51 60 ATCIC ATC INC 1.750 0.61 0.38 0.00 26.63 0.68 3.47 0.74 60 ATNN ATNN INC 0.219 1.38 1.5 0.00 50.89 1.30 6.64 1.25 60 ATTNF ATTN AVECA 1.750 2.81 0.39 0.05 42.49 1.59 6.97 2.20 39 ENTERTAINMENT COR AVSY AVTR SYS INC 0.203 -0.54 6.23 0.06 55.49 3.33 14.41 -0.02 AWCSA AW COMPUTER 5.875 1.23 7.08 0.01 71.41 1.85 9.29 1.15 50 SYS INC CLASS A ARON AARON RENTS 13.125 0.92 -0.23 0.16 10.30 0.26 1.34 0.95 60 INC ABIX ABATIX ENVI- 1.750 0.00 0.36 0.03 17.54 0.67 2.96 0.34 37 RONMENTAL CORP ABT ABBOTT LABS 66.000 0.87 0.87 0.51 4.31 0.11 0.56 0.92 60 ABERF ABER RES LTD 0.969 1.53 3.52 0.02 29.18 1.11 4.93 1.35 37 AANB ABIGAIL ADAMS 11.000 -1.50 1.81 0.14 12.61 0.70 2.80 -0.66 24 NATL BANCORP ABBK ABINGTON BAN.5.875 1.37 -0.15 0.09 20.09 0.51 2.62 1.24 60 CORP INC ABD ABIOMED INC 13.000 1.08 1.04 0.07 18.21 0-4 2.43 1.05 57 ABY ABITIBI PRICE 12.625 0.65 -1.42 0.23 6.00 0.13 n sn 0.77 57 INC ABRI ABRAMS INDS 4.313 1.28 1.90 0.07 20.91 0.53 2.73 1.18 2 INC ACAP ACAP CORP 0.500 0.05 0.88 0.02 13.80 0.35 1.80 0.37 60 ACLE ACCEL 1NTL6.750 1.12 -0.66 0.20 11.10 0.28 1.45 1.08 60 CORP AKLM ACCLAIM EN-6.375 1.29 0.02 0.03 23.62 0.84 3.58 1.9 THT INC ACCU ACCUHEALTH 5.438 0.53 0.60 0.00 13.47 0.49 2.17 0.69 41 INC Based on S&P500 Index.Using Straight Regression. Page3 Source:Reprinted by permission.Copvright 1992 Merrill Lvnch.Pierce.Fenner Smith Incorporated. 图17一8 25

表17一3 包含100种证券的各证券组合的事前事后系数值 1947.7一1954.6 证券组合 术调整3系数 调整,3系数 1954.7-1961.6 1961.7一1968.6 (1) (2) (3) (4) (5) y 0,36 0.48 0.57 0.72 2 0.61 0.68 0.71 0.79 0.78 0.82 0.88 0.88 4 0.91 0.93 0.96 0.92 5 1.01 1.01 1.03 1.4 6 1.13 1.10 1.13 1.02 1.26 1.21 1.24 1.08 8 1.47 1.39 1.32 1.35 表17一3中的第5栏是用第3个7华间的数据计算的历史B系数。试比较 第2、第4、第5栏中未调整的历史B系数,可以看出这些数值都有不断向平 均值1.0趋近的倾向,因此,上述调整程序(方法)看来对预测未来期间的3 系数具有一定的价值。 上面的讨论似乎说明了这样一种观点:“真实的”B系数不仅会随时间的 改变而改变,而且还具有回复到平均值的倾向,因为某些极端的数值会随时间 缓和下去。如果一个公司的经营状况和财务状况使其股票的风险人大地不同于 其他公司,则随着时间的椎移,公司通过各种调整使其股票的风险更容易回到 而不是史远离市场的平均水平。3系数存在这种趋向性的根本原因正是这~经 济原因而非纯粹的简单的统计现象。然而,我]没有理由去指望所有股票的 “其实的”B系数都能以同样的速度和相同的方式趋向相同的平均值,因此, 许多对公司的基本分析也许要比采用更复杂的统计方法处理过去的价格数据以 计算B系数更为行州。 虽然证券组合的历史B系数能对其未米B系数的预测提供有用的信总,但 单个正券的历史3系数却存在很大的误差,需要作相应处厘。这一点可以从 图17一8中所列的贝塔系数的标准误差项中不难看出。 表17一4提供了另外·种观察此问题的角度。该表将在纽约股票交易所上 市的所有股票,从1931年到1967什,逐年用其前5年的历史数据计算历史3 系数,然后逐年按1月份的历史B系数的高低将每支股票划入各个不同B等级 的组中。划分方法是在【月份的阝值为前10%的股票划入第10组,接下来的 10%划入第9组,以后照此类推。该表显示了5年以后仍在同·个组(第1 栏)和同个风险级别(第3栏)的股票的百分比。表中还显示了在这种过去 和未来的3分组没有关联的条件下可以预期到的百分比。检查该表可以发现, 个别证券的B系数具有某种程度的预测价值,但并不是很大。 26