
第十—章一元多项式的因式分解 1.基本内容 一元多项式、整除的概念、最大公因式、因式分解定理、重因式、多项式的根、复系数与 实系数多项式、有理系数多项式。 2.教学基本要求 掌握辗转相除法求多项式的最大公因式,掌握因式分解定理和重因式的概念,以及不可约 多项式的判断。 3.教学重点与难点 重点:辗转相除法,因式分解定理和多项式根的判断 难点:辗转相除法 第十二章多元多项式 1.基本内容 多元多项式、对称多项式。 2.教学基本要求 掌握字典排序法和其次多项式的概念,掌握初等多项式定义和对称多项式基本定理 3.教学重点与难点 重点:字典排序法,对称多项式基本定理 难点:对称多项式基本定理 4.教学建议 采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第十三章多项式矩阵与若尔当典范形 1.基本内容 多项式矩阵、不变因子、矩阵相似的条件、初等因子、若尔当典范形、矩阵的极小多项 式。 2.教学基本要求 掌握矩阵的初等变换和的方法,掌握矩阵相似的条件和若尔当典范形的概念。 3.教学重点与难点 重点:矩阵的初等变换,史密斯正规化 难点:矩阵的初等变换 4.敦学建议: 采用讲授法、提问法、课堂讨论法开展本章课程的学习。 四、教学环节与学时分配 27
27 第十一章 一元多项式的因式分解 1.基本内容 一元多项式、整除的概念、最大公因式、因式分解定理、重因式、多项式的根、复系数与 实系数多项式、有理系数多项式。 2.教学基本要求 掌握辗转相除法求多项式的最大公因式,掌握因式分解定理和重因式的概念,以及不可约 多项式的判断。 3.教学重点与难点 重点:辗转相除法,因式分解定理和多项式根的判断 难点:辗转相除法 第十二章 多元多项式 1.基本内容 多元多项式、对称多项式。 2.教学基本要求 掌握字典排序法和其次多项式的概念,掌握初等多项式定义和对称多项式基本定理 3.教学重点与难点 重点:字典排序法,对称多项式基本定理 难点:对称多项式基本定理 4.教学建议: 采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第十三章 多项式矩阵与若尔当典范形 1.基本内容 多项式矩阵、不变因子、矩阵相似的条件、初等因子、若尔当典范形、矩阵的极小多项 式。 2.教学基本要求 掌握矩阵的初等变换和的方法,掌握矩阵相似的条件和若尔当典范形的概念。 3.教学重点与难点 重点:矩阵的初等变换,史密斯正规化 难点:矩阵的初等变换 4.教学建议: 采用讲授法、提问法、课堂讨论法开展本章课程的学习。 四、教学环节与学时分配
总学 课外辅 教学内容 中 导1 号 课外实 备注 176 讲课 上机 其他 践 向量代数 16 16 2 行列式 1616 3线性方程组与线性子空间 16 16 4几何中的平面与直线 10 10 5 矩阵的秩与矩阵的运昇 16 16 6 钱性空问与欧儿里得空问 44 7 儿何空间的常见曲面 10 10 8 线性变换 1616 9 钱性空间上的函致 14 14 10 坐标变换与点变换 8 8 11 元多项式的因式分解 16 12 多元多项式 10 10 13多项式矩阵与若尔当典范型1414 五、教学中应注意的问题 高等代数与空间解析几何比较抽象,学生从中学刚进入大学,要采取适当的教学方法让学 生尽逐步话应。 六、实验实践内容 无 七、考核方式 见《高等代数与解析几何》课程考试大纲。 八、教材及主要参考书 1、选用教材: 《高等代数与解析几何》陈志杰主编,高等教育出版社,2008年 2.主要参考书: 山《高等代数》(第三版)北京大学数学系几何与代数教研室代数小组主编,高等教有 出版社,1998年. 2)《高等代数》张禾瑞,郝炳新主编,高等教育出版社。 [3】《高等代数》王萼芳主编,高等教有出版社 [4《解析几何》丘维生北京大学出版社1986 28
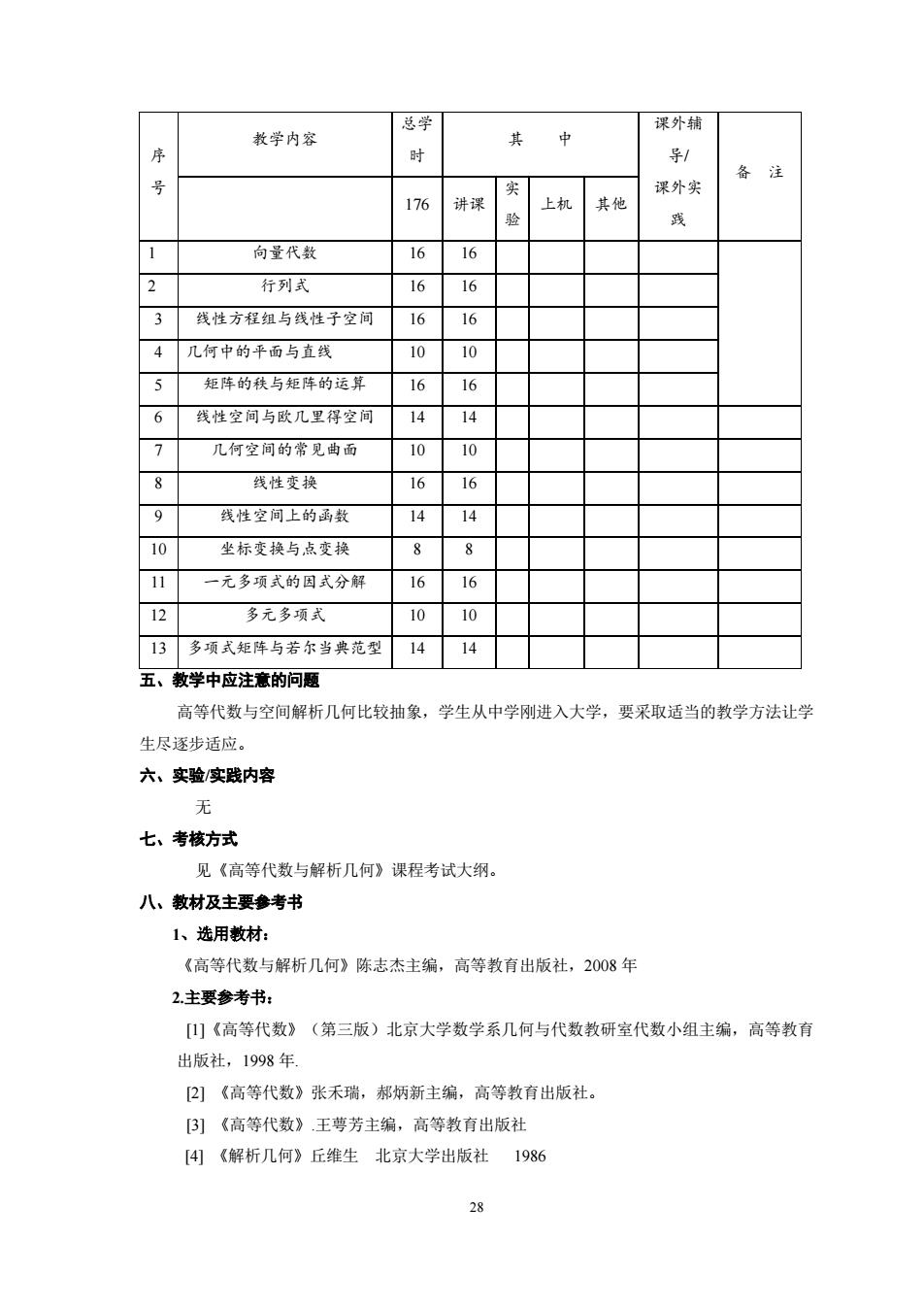
28 序 号 教学内容 总学 时 其 中 课外辅 导/ 课外实 践 备 注 176 讲课 实 验 上机 其他 1 向量代数 16 16 2 行列式 16 16 3 线性方程组与线性子空间 16 16 4 几何中的平面与直线 10 10 5 矩阵的秩与矩阵的运算 16 16 6 线性空间与欧几里得空间 14 14 7 几何空间的常见曲面 10 10 8 线性变换 16 16 9 线性空间上的函数 14 14 10 坐标变换与点变换 8 8 11 一元多项式的因式分解 16 16 12 多元多项式 10 10 13 多项式矩阵与若尔当典范型 14 14 五、教学中应注意的问题 高等代数与空间解析几何比较抽象,学生从中学刚进入大学,要采取适当的教学方法让学 生尽逐步适应。 六、实验/实践内容 无 七、考核方式 见《高等代数与解析几何》课程考试大纲。 八、教材及主要参考书 1、选用教材: 《高等代数与解析几何》陈志杰主编,高等教育出版社,2008 年 2.主要参考书: [1]《高等代数》(第三版)北京大学数学系几何与代数教研室代数小组主编,高等教育 出版社,1998 年. [2] 《高等代数》张禾瑞,郝炳新主编,高等教育出版社。 [3] 《高等代数》.王萼芳主编,高等教育出版社 [4] 《解析几何》丘维生 北京大学出版社 1986

[⑤《空间解析几何》复旦大学数学教研室:人民教有出版社1990 [宋卫东等,空间解析几何习题课设计与解题指导。合肥:中国科学技术大学出版社, 1995 九、教改说明及其他: 无 执笔人:刘艳琪系室审核人:许友军 29
29 [5]《空间解析几何》复旦大学数学教研室: 人民教育出版社 1990 [6]宋卫东等,空间解析几何习题课设计与解题指导。合肥:中国科学技术大学出版社, 1995 九、教改说明及其他: 无 执笔人:刘艳琪 系室审核人:许友军

《高等代数与解析几何》课程考试大纲 Advanced Algebra and Analytic Geometry 课程编号:170701011,170701012 总学时数:176学时 学分:11学分 一、考试对象:信息与计算科学专业的学生 二、考试目的 本考试科目目的在于考查考生高等代数与解析几何的基本概念、基本理论和基本方法的 掌握程度,检查学生在修完该课题后对所学内容的掌握情况。 三、考试要求 要求考生比较系统地理解高等代数与解析几何的基本概念和基本理论,掌握高等代数的基 本思想和方法。要求考生具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识 分析问题和解决问题的能力。 四、考试内容与要求 第一章向量代数 15分值 1考试内容:①向量的概念,向量的运算及矢向量的坐标法:②向量的内积和外积的基本 性质和运算规律,向量的混合积的概念及其性质③向量的内积、外积、混合积的坐标计算, 及其运算的几何意义。 2.考试要求:①向量的概念,向量的运算及矢量的坐标法:②向量的内积和外积的基本性 质和运算规律,向量的混合积的概念及其性质:③向量的内积、外积、混合积的坐标计算,及 其运算的几何意义。 第二章行列式18分值 1考试内容:行列式的概念和基本性质行列式计算行列式按行(列)展开定理拉普拉斯 (Laplace)定理及行列式的乘法法则 2.考试要求:1.理解行列式的概念,掌握行列式的性质、拉普拉斯Laplac©)定理及行列式 的乘法法则:2.会应用行列式概念和基本性质计算行列式,能够熟练掌握行列式按行(列)展开 定理,能够运用递推公式计算一些经典类型的行列式。 第三章线性方程组与线性子空间15分值 1、考试内容:①线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条 件:②非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组 的基础解系和通解解空间及其维数非齐次线性方程组的通解:③线性子空间的概念,以及基和 维数的求法。 30
30 《高等代数与解析几何》课程考试大纲 Advanced Algebra and Analytic Geometry 课程编号:170701011, 170701012 总学时数:176 学时 学分:11 学分 一、考试对象:信息与计算科学专业的学生 二、考试目的 本考试科目目的在于考查考生高等代数与解析几何的基本概念、基本理论和基本方法的 掌握程度,检查学生在修完该课题后对所学内容的掌握情况。 三、考试要求 要求考生比较系统地理解高等代数与解析几何的基本概念和基本理论,掌握高等代数的基 本思想和方法。要求考生具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识 分析问题和解决问题的能力。 四、考试内容与要求 第一章 向量代数 15 分值 1.考试内容:①向量的概念,向量的运算及矢向量的坐标法;②向量的内积和外积的基本 性质 和运算规律,向量的混合积的概念及其性质③向量的内积、外积、混合积的坐标计算, 及其运算的几何意义。 2.考试要求:①向量的概念,向量的运算及矢量的坐标法;②向量的内积和外积的基本性 质和运算规律,向量的混合积的概念及其性质;③向量的内积、外积、混合积的坐标计算,及 其运算的几何意义。 第二章 行列式 18 分值 1.考试内容:行列式的概念和基本性质行列式计算行列式按行(列)展开定理拉普拉斯 (Laplace)定理及行列式的乘法法则 2.考试要求: 1.理解行列式的概念,掌握行列式的性质、拉普拉斯(Laplace)定理及行列式 的乘法法则;2.会应用行列式概念和基本性质计算行列式,能够熟练掌握行列式按行(列)展开 定理,能够运用递推公式计算一些经典类型的行列式。 第三章 线性方程组与线性子空间 15 分值 1、考试内容:①线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条 件;②非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组 的基础解系和通解解空间及其维数非齐次线性方程组的通解;③线性子空间的概念,以及基和 维数的求法

2、考试要求:①会用克莱姆法则求解线性方程组:②掌捏齐次线性方程组有非零解的充 分必要条件及非齐次线性方程组有解的充分必要条件:③熟练掌握齐次线性方程组的基础解 系、通解及解空间的概念,掌握齐次线性方程组的基础解系和通解的求法:④理解非齐次线 性方程组解的结构及通解的概念:⑤掌握用初等行变换求解线性方程组的方法:©掌握齐次线 性方程组与非齐次线性方程组的解的结构,线性流形的概念。 第四章几何空间中的平面与直线16分值 1、考试内容:平面与空间曲线方程,空间中的点、直线、平面两两之间的相互关系的代 数形式的联系。掌握各种形式的直线方程和平面方程的表达方式,掌握直线与直线、平面与平 面、直线与平面间的位置关系的判断,掌握点、直线、平面之间的度量关系的计算。 2、考试要求:理解并熟练掌握利用向量建立平面和直线的向量式方程和坐标式方程,掌 握平面和直线方程的各种表示形式,能根据所给的条件建立适当的平面或直线的方程:掌握平 面与平面、直线与平面、直线与直线的各种位置关系及其判断方法,掌握有关的计算公式,能 根据所给的条件进行正确的论证和计算:理解平面束的概念,能利用平面束来解决有关的问 第五章矩阵的秩与矩阵的运算18分值 1、考试内容:矩阵的概念矩阵的基本运算矩阵的转置伴随矩阵逆矩阵的概念和性质矩阵 可逆的充分必要条件矩阵的初等变换和初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算 2、考试要求:①理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对 称矩阵和反对称矩阵,熟悉它们的基本性质:②掌握矩阵的数乘、加法、乘法、转置等运算。 了解方阵的多项式概念:③理解逆矩阵的概念,掌握可逆矩阵的性质,以及矩阵可逆的判别条 件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵:④掌握矩阵的初等变换、初等矩阵的性质 和矩阵等价的条件,理解矩阵的秩的概念,了解矩阵的秩与行列式的关系。了解矩阵乘积的秩 与因子矩阵的秩的关系,了解阶方阵非退化的概念及充分必要条件,熟练掌握用初等变换求 矩阵的秩和逆矩阵的方法:⑥熟悉分块矩阵及其运算。 第六章线性空间与欧几里德空间18分值 1、考试内容:①集合与映射的基本概念线性空间的概念与基本性质线性空间的维数、基 与向量的坐标线性空间中的基变换与坐标变换过渡矩阵线性子空间及其运算线性空间的同构: ②线性空间内积的定义及其性质欧几里德空间的概念标准(规范)正交基施密特(Schmidt)正交化 过程正交矩阵正交变换及其性质正交子空间、正交补及其性质实对称矩阵的特征值、特征向量 及相似对角矩阵欧几里德空间的同构。 2、考试要求:①理解线性空间的概念掌握线性子空间的判定方法,掌握线性空间的维 数、基和坐标等基本概念和性质,了解线性空间同构的概念,了解同构映射的性质:②理解生 成子空间的概念,掌握求子空间基和维数的方法,掌握子空间的交、和、直积运算及其性质, 了解线性空间同构的概念,了解同构映射的性质:③理解和掌握标准(规范)正交基的概念,掌 3
31 2、考试要求:①会用克莱姆法则求解线性方程组;②掌握齐次线性方程组有非零解的充 分必要条件及非齐次线性方程组有解的充分必要条件; ③熟练掌握齐次线性方程组的基础解 系、通解及解空间的概念,掌握齐次线性方程组的基础解系和通解的求法; ④理解非齐次线 性方程组解的结构及通解的概念;⑤掌握用初等行变换求解线性方程组的方法;⑥掌握齐次线 性方程组与非齐次线性方程组的解的结构,线性流形的概念。 第四章 几何空间中的平面与直线 16 分值 1、考试内容 :平面与空间曲线方程,空间中的点、直线、平面两两之间的相互关系的代 数形式的联系。掌握各种形式的直线方程和平面方程的表达方式,掌握直线与直线、平面与平 面、直线与平面间的位置关系的判断,掌握点、直线、平面之间的度量关系的计算。 2、考试要求:理解并熟练掌握利用向量建立平面和直线的向量式方程和坐标式方程,掌 握平面和直线方程的各种表示形式,能根据所给的条件建立适当的平面或直线的方程;掌握平 面与平面、直线与平面、直线与直线的各种位置关系及其判断方法,掌握有关的计算公式,能 根据所给的条件进行正确的论证和计算;理解平面束的概念,能利用平面束来解决有关的问 题。 第五章 矩阵的秩与矩阵的运算 18 分值 1、考试内容:矩阵的概念矩阵的基本运算矩阵的转置伴随矩阵逆矩阵的概念和性质矩阵 可逆的充分必要条件矩阵的初等变换和初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算 2、考试要求:①理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对 称矩阵和反对称矩阵,熟悉它们的基本性质;②掌握矩阵的数乘、加法、乘法、转置等运算。 了解方阵的多项式概念;③理解逆矩阵的概念,掌握可逆矩阵的性质,以及矩阵可逆的判别条 件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵;④掌握矩阵的初等变换、初等矩阵的性质 和矩阵等价的条件,理解矩阵的秩的概念,了解矩阵的秩与行列式的关系。了解矩阵乘积的秩 与因子矩阵的秩的关系,了解 n 阶方阵非退化的概念及充分必要条件,熟练掌握用初等变换求 矩阵的秩和逆矩阵的方法;⑥熟悉分块矩阵及其运算。 第六章 线性空间与欧几里德空间 18 分值 1、考试内容:①集合与映射的基本概念线性空间的概念与基本性质线性空间的维数、基 与向量的坐标线性空间中的基变换与坐标变换过渡矩阵线性子空间及其运算线性空间的同构; ②线性空间内积的定义及其性质欧几里德空间的概念标准(规范)正交基施密特(Schmidt)正交化 过程正交矩阵正交变换及其性质正交子空间、正交补及其性质实对称矩阵的特征值、特征向量 及相似对角矩阵欧几里德空间的同构。 2、考试要求:①理解线性空间的概念掌握线性子空间的判定方法,掌握线性空间的维 数、基和坐标等基本概念和性质,了解线性空间同构的概念,了解同构映射的性质;②理解生 成子空间的概念,掌握求子空间基和维数的方法,掌握子空间的交、和、直积运算及其性质, 了解线性空间同构的概念,了解同构映射的性质;③理解和掌握标准(规范)正交基的概念,掌