
(1)第一型曲面积分 第一型曲面积分的概念:第一型曲面积分的计算 (2)第二型曲面积分 曲面的侧:第二型曲面积分的概念:第二型曲面积分的计算:两类曲面的关系 (3)高斯公式与斯托克斯公式 (4)场论初步 场的概念:梯度场:散度场:旋渡场:管量场与有势场 2.教学基本要求: (1)掌握有关实数绝对值的性质与运算: (2)深刻理解确界概念与确界原理,并能运用有关命题进行运算与证明: (3)深刻理解函数概念,进一步了解函数概念,进一步了解函数的几种表示法和几种具 有某些特性的函数。 3教学重点难点: 重点:掌握第一型曲面积分与第二型曲面积分的概念与计算,理解第一型曲面积分与第二 型曲面积分二者之间形式上的转化关系,掌握奥一高公式、斯托克斯公式。 难点:曲面的侧在积分中的运用。 4.教学建议: 采用讲授法、提问法、课堂讨论法开展本章课程的学习。 四、教学环节与学时分配 总 课外辅 教学内容 学 其 备 序号 果外实 实上其 272 讲课 他 第一章 实数集与函数 10 8 2 第二章 数列极限 16 12 4 第三章 函数极限 16 12 4 第四章 函数的连续性 12 3 第五章 导数和微分 14 10 4 第六 微分中值定理及其应用 16 10 6 第七章 实数的完备性 10 3 第八章 不定积分 12 8 4 第九章 定积分 16 10 6 2
12 (1)第一型曲面积分 第一型曲面积分的概念;第一型曲面积分的计算 (2)第二型曲面积分 曲面的侧;第二型曲面积分的概念;第二型曲面积分的计算;两类曲面的关系 (3)高斯公式与斯托克斯公式 (4)场论初步 场的概念;梯度场;散度场;旋渡场;管量场与有势场 2.教学基本要求: (1)掌握有关实数绝对值的性质与运算; (2)深刻理解确界概念与确界原理,并能运用有关命题进行运算与证明; (3)深刻理解函数概念,进一步了解函数概念,进一步了解函数的几种表示法和几种具 有某些特性的函数。 3.教学重点难点: 重点: 掌握第一型曲面积分与第二型曲面积分的概念与计算,理解第一型曲面积分与第二 型曲面积分二者之间形式上的转化关系,掌握奥—高公式、斯托克斯公式。 难点: 曲面的侧在积分中的运用。 4.教学建议: 采用讲授法、提问法、课堂讨论法开展本章课程的学习。 四、教学环节与学时分配 序号 教学内容 总 学 时 其 中 课外辅 导/ 课外实 践 备 注 272 讲课 实 验 上 机 其 他 第一章 实数集与函数 10 8 2 第二章 数列极限 16 12 4 第三章 函数极限 16 12 4 第四章 函数的连续性 12 9 3 第五章 导数和微分 14 10 4 第六章 微分中值定理及其应用 16 10 6 第七章 实数的完备性 10 7 3 第八章 不定积分 12 8 4 第九章 定积分 16 10 6
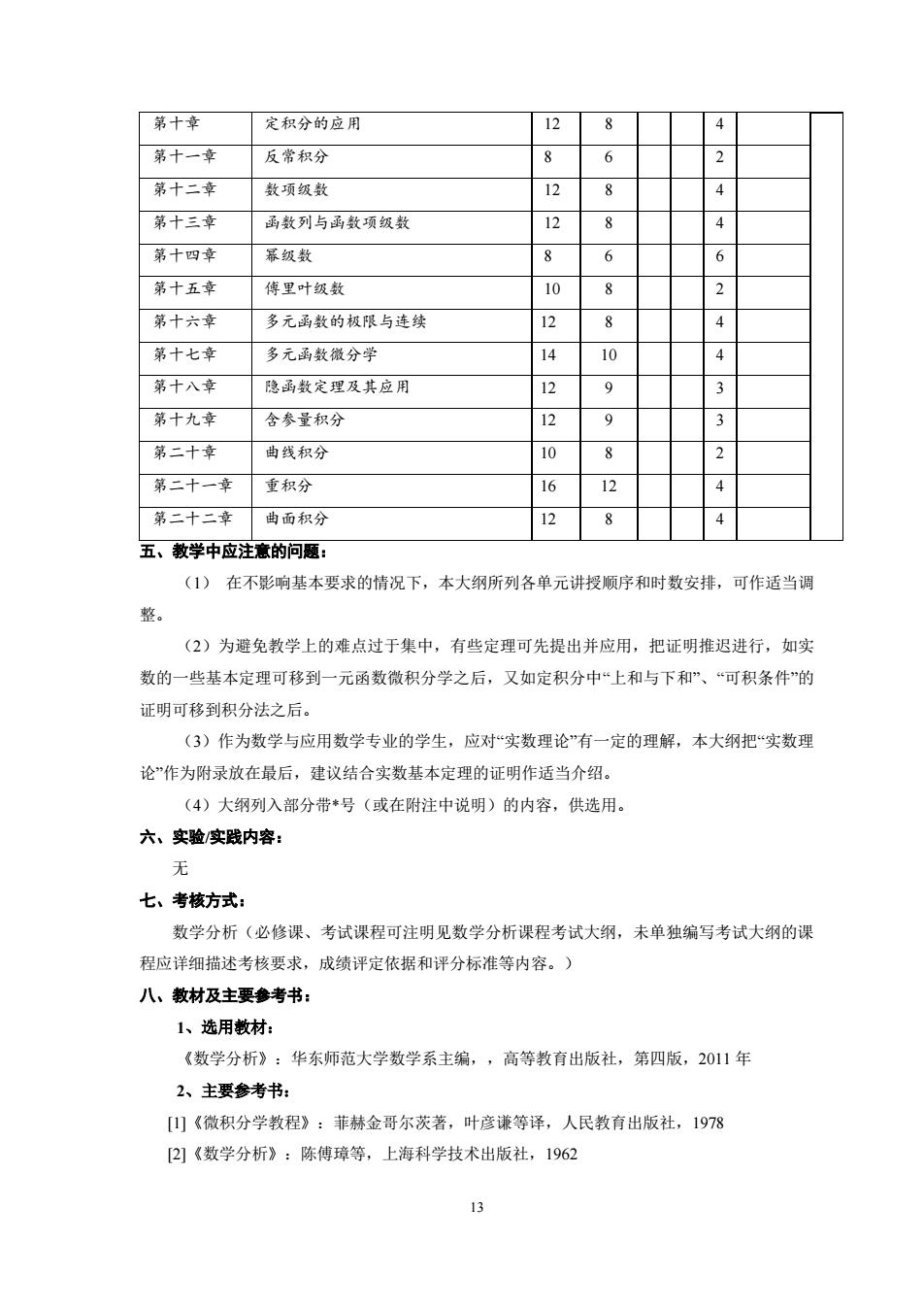
第十章 定积分的应用 12 4 第十一章 反常积分 第十二章 数项级数 12 4 第十三章 函数列与函数项级数 12 4 第十四章 暴级数 6 第十五章 傅里叶级数 10 2 第十六章 多元函数的极限与连续 12 8 4 第十七章 多元函数微分学 10 4 第十八章 隐函数定理及其应用 12 9 3 第十九章 含参量积分 9 第二十章 曲线积分 10 8 2 第二十一章 重根分 16 12 第二十二章 曲面积分 2 8 4 五、教学中应注意的问题: (1)在不影响基本要求的情况下,本大纲所列各单元讲授顺序和时数安排, 可作适当调 (2)为避免教学上的难点过于集中,有些定理可先提出并应用,把证明推迟进行,如实 数的一些基本定理可移到一元函数微积分学之后,又如定积分中“上和与下和”、“可积条件”的 证明可移到积分法之后。 (3)作为数学与应用数学专业的学生,应对“实数理论”有一定的理解,本大纲把“实数理 论”作为附录放在最后,建议结合实数基本定理的证明作适当介绍。 (4)大纲列入部分带*号(或在附注中说明)的内容,供选用。 六、实验实践内容: 无 七、考核方式: 数学分析(必修课、考试课程可注明见数学分析课程考试大纲,未单独编写考试大纲的课 程应详细描述考核要求,成绩评定依据和评分标准等内容。) 八、教材及主要参考书: 1、选用教材: 《数学分析》:华东师范大学数学系主编,,高等教有出版社,第四版,2011年 2、主要参考书: [山《微积分学教程》:菲赫金哥尔茨著,叶彦谦等译,人民教有出版社,1978 2《数学分析》:陈傅璋等,上海科学技术出版社,1962 13
13 第十章 定积分的应用 12 8 4 第十一章 反常积分 8 6 2 第十二章 数项级数 12 8 4 第十三章 函数列与函数项级数 12 8 4 第十四章 幂级数 8 6 6 第十五章 傅里叶级数 10 8 2 第十六章 多元函数的极限与连续 12 8 4 第十七章 多元函数微分学 14 10 4 第十八章 隐函数定理及其应用 12 9 3 第十九章 含参量积分 12 9 3 第二十章 曲线积分 10 8 2 第二十一章 重积分 16 12 4 第二十二章 曲面积分 12 8 4 五、教学中应注意的问题: (1) 在不影响基本要求的情况下,本大纲所列各单元讲授顺序和时数安排,可作适当调 整。 (2)为避免教学上的难点过于集中,有些定理可先提出并应用,把证明推迟进行,如实 数的一些基本定理可移到一元函数微积分学之后,又如定积分中“上和与下和”、“可积条件”的 证明可移到积分法之后。 (3)作为数学与应用数学专业的学生,应对“实数理论”有一定的理解,本大纲把“实数理 论”作为附录放在最后,建议结合实数基本定理的证明作适当介绍。 (4)大纲列入部分带*号(或在附注中说明)的内容,供选用。 六、实验/实践内容: 无 七、考核方式: 数学分析(必修课、考试课程可注明见数学分析课程考试大纲,未单独编写考试大纲的课 程应详细描述考核要求,成绩评定依据和评分标准等内容。) 八、教材及主要参考书: 1、选用教材: 《数学分析》:华东师范大学数学系主编,,高等教育出版社,第四版,2011 年 2、主要参考书: [1]《微积分学教程》:菲赫金哥尔茨著,叶彦谦等译,人民教育出版社,1978 [2]《数学分析》:陈傅璋等,上海科学技术出版社,1962

3)《数学分析》:欧阳光中等,上海科学技术出版社,1982。 [4]《数学分析讲义(第三版)》:刘玉琏等,高等教有出版社,1992。 [们《数学分析教程》:常庚哲等,高等教有出版社,2003。 九、教改说明及其他: 无 执笔人:许友军系室审核人:刘亚春 4
14 [3]《数学分析》:欧阳光中等,上海科学技术出版社,1982。 [4]《数学分析讲义(第三版)》:刘玉琏等,高等教育出版社,1992。 [5]《数学分析教程》:常庚哲等,高等教育出版社,2003。 九、教改说明及其他: 无 执笔人:许友军 系室审核人:刘亚春

《数学分析》课程考试大纲 Mathematical Analysis 课程编号:170701009,170701010,130701040 总学时数:272学时 学分:17学分 一、考试对象 信息与计算科学专业 二、考试目的 本课程考试目的是检查学生掌握变量与函数、极限与连续、导数与微分、微分学的基本定 理、不定积分等内容的基本情况。 三、考试要求 本课程是一门理论性很强的基础性学科,要求学生掌握基本理论,其备较强的分析、计 算、推理及应用能力。 四、考试内容与要求 第一章实数集与函数8-15分值 1、考试内容:实数及其性质,绝对值与不等式。区间与邻域,有界集与确界原理。函数概 念,函数的表示法。函数的四则运算,复合函数反函数,初等函数。具有某些特性的函数:有界函 数、单调函数、奇函数与偶函数、周期函数。 2、考试要求:了解实数及其性质:理解区间与邻域的概念,理解绝对值与不等式的性 质,会解绝对值与不等式:理解确界概念及确界原理,会用确界概念证明某些问题:深刻理解 “映射“观点下的一元函数概念:深刻理解函数的四则运算、复合函数、反函数、初等函数及基 本初等函数的概念,熟练掌握函数的复合运算:理解函数的有界性、单调性、奇偶性和周期性 概念,并会用定义判新一个函数是否具有这些性质:了解并记住一些非初等函数,例如整数部 分函数、符号函数、狄利克雷函数 第二章数列极限815分值 1、考试内容:数列。数列极限的8N定义,无穷小数列。收敛数列性质:唯一性、有界性、保 号性、不等式性质、迫敛性、四则运算法则。子列及子列定理。数列极限存在的条件:数列极 限的单调有界定理、柯西收敛准则。 2、考试要求:深刻理解数列极限的N定义及它的几何意义,它的几何意义:了解无穷 小数列、子列及子列定理:深刻理解收敛数列性质,并掌握其应用:理解数列极限存在的条 件,并学会它的一些应用:熟练掌握数列极限的运算。 第三章函数极限&-15分值 1、考试内容:x→0时函数的极限,x→x。时函数的极限,单侧极限。函数极限的性 质:唯一性、局部有界性、局部保号性、不等式性质、迫敛性和四则运算法则。函数极限存在 15
15 《数学分析》课程考试大纲 Mathematical Analysis 课程编号:170701009, 170701010,130701040 总学时数:272 学时 学分:17 学分 一、 考试对象 信息与计算科学专业 二、考试目的 本课程考试目的是检查学生掌握变量与函数、极限与连续、导数与微分、微分学的基本定 理、不定积分等内容的基本情况。 三、考试要求 本课程是一门理论性很强的基础性学科,要求学生掌握基本理论,具备较强的分析、计 算、推理及应用能力。 四、考试内容与要求 第一章 实数集与函数 8-15 分值 1、考试内容:实数及其性质,绝对值与不等式。区间与邻域,有界集与确界原理。函数概 念,函数的表示法。函数的四则运算,复合函数,反函数,初等函数。具有某些特性的函数:有界函 数、单调函数、奇函数与偶函数、周期函数。 2、考试要求:了解实数及其性质;理解区间与邻域的概念,理解绝对值与不等式的性 质,会解绝对值与不等式;理解确界概念及确界原理,会用确界概念证明某些问题;深刻理解 “映射”观点下的一元函数概念;深刻理解函数的四则运算、复合函数、反函数、初等函数及基 本初等函数的概念,熟练掌握函数的复合运算;理解函数的有界性、单调性、奇偶性和周期性 概念,并会用定义判断一个函数是否具有这些性质;了解并记住一些非初等函数,例如整数部 分函数、符号函数、狄利克雷函数。 第二章 数列极限 8-15 分值 1、考试内容:数列。数列极限的 ε-N 定义,无穷小数列。收敛数列性质:唯一性、有界性、保 号性、不等式性质、迫敛性、四则运算法则。子列及子列定理。数列极限存在的条件:数列极 限的单调有界定理、柯西收敛准则。 2、考试要求:深刻理解数列极限的 ε-N 定义及它的几何意义, 它的几何意义;了解无穷 小数列、子列及子列定理;深刻理解收敛数列性质,并掌握其应用;理解数列极限存在的条 件,并学会它的一些应用;熟练掌握数列极限的运算。 第三章 函数极限 8-15 分值 1、考试内容: x 时函数的极限, 0 x x 时函数的极限,单侧极限。函数极限的性 质:唯一性、局部有界性、局部保号性、不等式性质、迫敛性和四则运算法则。函数极限存在

的条件:归结原则、函数极限的单调有界定理和柯西准则。两个重要极限。无穷小量及其阶的 比较,无穷大量,曲线的渐近线。 2、考试要求:深刻理解各种趋势函数极限(包括单侧极限)的定义,以及它们的几何意 义,并会用6一6,5一M定义及其否定叙述证明某些函数的极限:深刻理解函数极限的性质, 并掌握其应用:理解函数极限的存在的条件,并学会它的一些应用。理解两个重要极限,并堂 握熟练它们的应用:理解无穷小量、无穷大量的概念,掌握无穷小阶的比较,并会使用兰道符 号。会用等价无穷小求极限:会求曲线的渐近线:熟练掌握函数极限的运算。 第四章函数的连续性8-15分值 1、考试内容:函数在一点的连续性,左、右连续,间断点及其分类,区间上的连续函数。连 续函数的局部性质:局部有界性、局部保号性、四则运算、复合函数的连续性,闭区间上连续 函数的性质:最值定理、介值性定理、根的存在定理,反函数的连续性,一致连续与一致连续性 定理。指数函数的连续性,初等函数连续性。 2、考试要求:深刻理解函数在一点连续(包括单侧连续),以及在在区间上连续的概 念,并能用定义证明函数在一点是否连续:掌握不连续点的判断方法及其分类:理解连续函数 的局部性质,并掌握其应用:理解闭区间上连续函数的性质、反函数的连续性,一致连续与一致 连续性定理,初等函数连续性,并掌握其应用。 第五章导数与微分8-15分值 1、考试内容:导数的定义,导函数,导数的几何意义,极值,费马定理。导数的四则运 算法则,反函数的导数,复合函数的导数,基本求导法则与公式。参变量函数的导数,隐函数的 导数,初等函数的导数。高阶导数。微分概念,微分的几何意义,微分的运算法则,一阶微分 形式的不变性,高阶微分,微分在近似计算中的应用。 2、考试要求:深刻理解导数的概念及其几何意义,了解导数的物理意义。会求平面曲线 的切线方程和法线方程:深刻理解函数的可导性与连续性之间的关系:掌握利用导数定义计算 函数(含分段函数)的导数(包括单侧导数),熟练掌握导数基本公式和求导法则(四则运算、反 函数、复合函数、隐函数及用参数方程表示的函数的求导法则):掌握隐函数和由参数方程所 确定的函数的一阶、二阶导数:深刻理解微分的概念、微分的几何意义以及导数与微分的异 同:熟练掌握微分运算,理解一阶微分形式的不变性,了解微分在近似计算中的应用:理解函 数的高阶导数和高阶微分概念,掌握高阶导数和高阶微分的求法。会应用莱不尼兹公式计算两 个函数乘积的高阶导数:理解极值概念和费马定理 第六章微分中值定理及其应用815分值 1、考试内容:罗尔中值定理,拉格朗日中值定理,单调函数。柯西中值定理。不定式极 限,罗比塔法则。带有皮亚诺(Peao)型余项、拉格朗日型余项的泰勒公式,泰勒公式在近 似计算上的应用。函数单调性与极值。最大值与最小值。函数的凸性与曲线的拐点。函数图象 的讨论。方程的近似解幸。 16
16 的条件:归结原则、函数极限的单调有界定理和柯西准则。两个重要极限。无穷小量及其阶的 比较,无穷大量,曲线的渐近线。 2、考试要求:深刻理解各种趋势函数极限(包括单侧极限)的定义,以及它们的几何意 义,并会用 , M 定义及其否定叙述证明某些函数的极限;深刻理解函数极限的性质, 并掌握其应用;理解函数极限的存在的条件,并学会它的一些应用。理解两个重要极限,并掌 握熟练它们的应用;理解无穷小量、无穷大量的概念,掌握无穷小阶的比较,并会使用兰道符 号。会用等价无穷小求极限;会求曲线的渐近线;熟练掌握函数极限的运算。 第四章 函数的连续性 8-15 分值 1、考试内容:函数在一点的连续性,左、右连续,间断点及其分类,区间上的连续函数。连 续函数的局部性质:局部有界性、局部保号性、四则运算、复合函数的连续性,闭区间上连续 函数的性质:最值定理、介值性定理、根的存在定理,反函数的连续性,一致连续与一致连续性 定理。指数函数的连续性,初等函数连续性。 2、考试要求:深刻理解函数在一点连续(包括单侧连续),以及在在区间上连续的概 念,并能用定义证明函数在一点是否连续;掌握不连续点的判断方法及其分类;理解连续函数 的局部性质,并掌握其应用;理解闭区间上连续函数的性质、反函数的连续性,一致连续与一致 连续性定理,初等函数连续性,并掌握其应用。 第五章 导数与微分 8-15 分值 1、考试内容:导数的定义,导函数,导数的几何意义,极值,费马定理。导数的四则运 算法则,反函数的导数, 复合函数的导数,基本求导法则与公式。参变量函数的导数,隐函数的 导数,初等函数的导数。高阶导数。微分概念,微分的几何意义,微分的运算法则,一阶微分 形式的不变性,高阶微分,微分在近似计算中的应用。 2、考试要求:深刻理解导数的概念及其几何意义,了解导数的物理意义。会求平面曲线 的切线方程和法线方程;深刻理解函数的可导性与连续性之间的关系;掌握利用导数定义计算 函数(含分段函数)的导数(包括单侧导数), 熟练掌握导数基本公式和求导法则(四则运算、反 函数、复合函数、隐函数及用参数方程表示的函数的求导法则); 掌握隐函数和由参数方程所 确定的函数的一阶、二阶导数;深刻理解微分的概念、微分的几何意义以及导数与微分的异 同;熟练掌握微分运算,理解一阶微分形式的不变性,了解微分在近似计算中的应用;理解函 数的高阶导数和高阶微分概念,掌握高阶导数和高阶微分的求法。会应用莱不尼兹公式计算两 个函数乘积的高阶导数;理解极值概念和费马定理。 第六章 微分中值定理及其应用 8-15 分值 1、考试内容:罗尔中值定理,拉格朗日中值定理,单调函数。柯西中值定理。不定式极 限,罗比塔法则。带有皮亚诺(Peano)型余项、拉格朗日型余项的泰勒公式,泰勒公式在近 似计算上的应用。函数单调性与极值。最大值与最小值。函数的凸性与曲线的拐点。函数图象 的讨论。方程的近似解