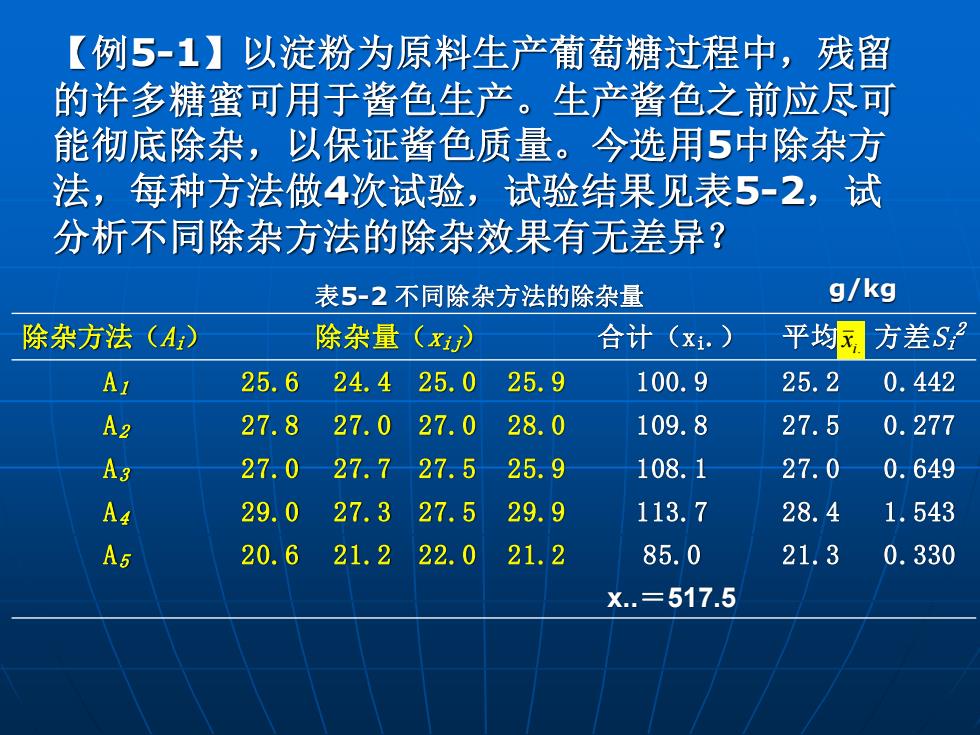
【例5-1】以淀粉为原料生产葡萄糖过程中,残留 的许多糖蜜可用于酱色生产。生产酱色之前应尽可 能彻底除杂,以保证酱色质量。今选用5中除杂方 法,每种方法做4次试验,试验结果见表5-2,试 分析不同除杂方法的除杂效果有无差异? 除杂方法(Ai) 除杂量(xij) 合计(xi.) 平均 方差Si 2 A1 25.6 24.4 25.0 25.9 100.9 25.2 0.442 A2 27.8 27.0 27.0 28.0 109.8 27.5 0.277 A3 27.0 27.7 27.5 25.9 108.1 27.0 0.649 A4 29.0 27.3 27.5 29.9 113.7 28.4 1.543 A5 20.6 21.2 22.0 21.2 85.0 21.3 0.330 x.=517.5 i. x 表5-2 不同除杂方法的除杂量 g/kg
【例5-1】以淀粉为原料生产葡萄糖过程中,残留 的许多糖蜜可用于酱色生产。生产酱色之前应尽可 能彻底除杂,以保证酱色质量。今选用5中除杂方 法,每种方法做4次试验,试验结果见表5-2,试 分析不同除杂方法的除杂效果有无差异? 除杂方法(Ai) 除杂量(xij) 合计(xi.) 平均 方差Si 2 A1 25.6 24.4 25.0 25.9 100.9 25.2 0.442 A2 27.8 27.0 27.0 28.0 109.8 27.5 0.277 A3 27.0 27.7 27.5 25.9 108.1 27.0 0.649 A4 29.0 27.3 27.5 29.9 113.7 28.4 1.543 A5 20.6 21.2 22.0 21.2 85.0 21.3 0.330 x.=517.5 i. x 表5-2 不同除杂方法的除杂量 g/kg

单因素试验,处理数k=5,重复数n=4。 各项偏差平方和及自由度计算如下: 矫正数 总偏差平方和 / 517.5 /(4 5) 13390.3125 2 2 C = x. nk = = 138.1975 25.6 24.4 21.2 13390.3125 2 2 2 2 = = + + + − = − SST xi j C 上一张 下一张 主 页 退 出
单因素试验,处理数k=5,重复数n=4。 各项偏差平方和及自由度计算如下: 矫正数 总偏差平方和 / 517.5 /(4 5) 13390.3125 2 2 C = x. nk = = 138.1975 25.6 24.4 21.2 13390.3125 2 2 2 2 = = + + + − = − SST xi j C 上一张 下一张 主 页 退 出

13518.7875 13390.3125 128.4750 (100.9 109.8 108.1 113.7 ) 4 1 . 1 2 2 2 2 2 = − = = + + + − = − C x C n SS i t 处理间(不同除杂方法间)的偏差平方和 处理内(误差)的偏差平方和 =138.1975−128.4750 = 9.7225 SSe = SST − SSt
13518.7875 13390.3125 128.4750 (100.9 109.8 108.1 113.7 ) 4 1 . 1 2 2 2 2 2 = − = = + + + − = − C x C n SS i t 处理间(不同除杂方法间)的偏差平方和 处理内(误差)的偏差平方和 =138.1975−128.4750 = 9.7225 SSe = SST − SSt

总自由度 处理间自由度 处理内自由度 用SSt、SSe分别除以dft和dfe便可得到处 理间均方MSt及处理内均方MSe。 dfT = nk −1= 45−1=19 dft = k −1= 5−1= 4 = − =19− 4 =15 e T t df df df / 9.7225/15 0.65 / 128.475/ 4 32.12 = = = = = = e e e t t t MS SS df MS SS df 上一张 下一张 主 页 退 出
总自由度 处理间自由度 处理内自由度 用SSt、SSe分别除以dft和dfe便可得到处 理间均方MSt及处理内均方MSe。 dfT = nk −1= 45−1=19 dft = k −1= 5−1= 4 = − =19− 4 =15 e T t df df df / 9.7225/15 0.65 / 128.475/ 4 32.12 = = = = = = e e e t t t MS SS df MS SS df 上一张 下一张 主 页 退 出

假设各处理没有真实差异,那么 和 都是误差方差 的估计量。以 为分母, 为分子,求其比值。统计学上把两个均方之 比值称为F值。即 1.2.2 构造F统计量,进行F检验 2 2 / F = St Se 1, ( 1) df1 = dft = k − df2 = dfe = k n − (1) F统计量构造 ~F(df1,df2) 2 St 2 Se 2 2 t S 2 e S
假设各处理没有真实差异,那么 和 都是误差方差 的估计量。以 为分母, 为分子,求其比值。统计学上把两个均方之 比值称为F值。即 1.2.2 构造F统计量,进行F检验 2 2 / F = St Se 1, ( 1) df1 = dft = k − df2 = dfe = k n − (1) F统计量构造 ~F(df1,df2) 2 St 2 Se 2 2 t S 2 e S