
第3章统计数据分布特征的描述 学习目标 1、孰练掌据反映续计数据分布华中鹊热的各种平均指标的汤义及其计算方法 2 熟练掌握反映统计数据分布离中趋势的各种变异指标的涵义及其计算方法 、熟练掌握反映统计数据分布对称与偏斜程度的偏度和峰度指标的涵义及其计算方法。 基本概念 位置平均数分位数数值平均数算术平均数几何平均数权数四分位差方差标准差 系数) 3.1统计变量集中趋势的测定 统计学是关于收集、分析、表述和解释统计数据的方法论科学,她对统计数据的收集、分析、表述 和解释虽然要从每一个数据着手,但其着眼点即研究目的却是在于统计数据整体或者说研究现象的总体 特征。在一个统计总体中,每一个个体即统计单位都有自己的特征和属性,具体地就表现出不同的标志 值,我们不能用其中的某一个或某几个的标志值来代表全部据的特征,而必须使用所有数据的代表值 来表述总体特征,这就必须测定变量的集中趋势。 3.1.1测定集中趋势的主要指标及其作用 集中趋势的描述是统计数据描述的重要内容。所谓集中是指数据向中心靠拢的意思,所以,集中趋 势也称为中心 位置。 统计数据的集中趋势(或中心位置)是指数据向其中心值靠拢或集中的程度。测定 集中趋势就是寻找数据水平的代表值或中心值。 测定集中趋势的指标有两类:位置平均数和数值平均数。 所谓位置平均数是根据变量值位置来确定的代表值,即在总体中将变量值按顺序排列得到的数列中 某个特殊位置的值就称为位置平均数。常用的位置平均数有众数、中位数和分位数等,前两种常用。位 置平均数可以用于对品质数据(由定类尺度和定序尺度所测量的数据即定类数据和顺序数据)和数量数 据(由定距尺度和定比尺度所测量的数据)的测度 所谓数值平均数就是均值 ,它是对总体中的所有数据计算平均值,用以反映所有数据的 般水平 根据计算方法不同,数值平均数可以分为算术平均数、调和平均数、几何平均数和幂平均数。这类平均 数的特点是,统计总体中任何一项数据的变动都会在一定程度上影响到数值平均数的计算结果。数值平 均数只能用于对数量数据的测度。 定集中静势是为了表示社会经济现象总体名单位某一标志在一定时间、地占条件下所达到的一般 水平。亦即将总体各单位标 值的 数量差异抽象化, 反映 总体在具体条件下各单位标志值达到的 一般力 平。集中趋势的指标经常被作为评价事物和决策的数量标准或参考。具体地说,测定集中趋势的作用如 下: 1.反映总体各单位变量分布的集中趋势和一般水平 实践中,客观现象总体各单位的某一变量值或从小到大、成按照某一特征形成一定的分布,通常标 志值很极端的单位数比较少,越靠近中心值单位数就越多,也就是说 围绕在中心值周围的标志值个数 在总体单位数中占有最大比重,显示总体各单位向中心值集中。所以集中趋势的测定指标是反映总休各
1 第 3 章 统计数据分布特征的描述 学习目标 1、熟练掌握反映统计数据分布集中趋势的各种平均指标的涵义及其计算方法; 2、熟练掌握反映统计数据分布离中趋势的各种变异指标的涵义及其计算方法; 3、熟练掌握反映统计数据分布对称与偏斜程度的偏度和峰度指标的涵义及其计算方法。 基本概念 位置平均数 分位数 数值平均数 算术平均数 几何平均数 权数 四分位差 方差 标准差 (系数) 3.1 统计变量集中趋势的测定 统计学是关于收集、分析、表述和解释统计数据的方法论科学,她对统计数据的收集、分析、表述 和解释虽然要从每一个数据着手,但其着眼点即研究目的却是在于统计数据整体或者说研究现象的总体 特征。在一个统计总体中,每一个个体即统计单位都有自己的特征和属性,具体地就表现出不同的标志 值,我们不能用其中的某一个或某几个的标志值来代表全部数据的特征,而必须使用所有数据的代表值 来表述总体特征,这就必须测定变量的集中趋势。 3.1.1 测定集中趋势的主要指标及其作用 集中趋势的描述是统计数据描述的重要内容。所谓集中是指数据向中心靠拢的意思,所以,集中趋 势也称为中心位置。统计数据的集中趋势(或中心位置)是指数据向其中心值靠拢或集中的程度。测定 集中趋势就是寻找数据水平的代表值或中心值。 测定集中趋势的指标有两类:位置平均数和数值平均数。 所谓位置平均数是根据变量值位置来确定的代表值,即在总体中将变量值按顺序排列得到的数列中 某个特殊位置的值就称为位置平均数。常用的位置平均数有众数、中位数和分位数等,前两种常用。位 置平均数可以用于对品质数据(由定类尺度和定序尺度所测量的数据即定类数据和顺序数据)和数量数 据(由定距尺度和定比尺度所测量的数据)的测度。 所谓数值平均数就是均值,它是对总体中的所有数据计算平均值,用以反映所有数据的一般水平。 根据计算方法不同,数值平均数可以分为算术平均数、调和平均数、几何平均数和幂平均数。这类平均 数的特点是,统计总体中任何一项数据的变动都会在一定程度上影响到数值平均数的计算结果。数值平 均数只能用于对数量数据的测度。 测定集中趋势是为了表示社会经济现象总体各单位某一标志在一定时间、地点条件下所达到的一般 水平。亦即将总体各单位标志值的数量差异抽象化,反映总体在具体条件下各单位标志值达到的一般水 平。集中趋势的指标经常被作为评价事物和决策的数量标准或参考。具体地说,测定集中趋势的作用如 下: 1.反映总体各单位变量分布的集中趋势和一般水平 实践中,客观现象总体各单位的某一变量值或从小到大、或按照某一特征形成一定的分布,通常标 志值很极端的单位数比较少,越靠近中心值单位数就越多,也就是说,围绕在中心值周围的标志值个数 在总体单位数中占有最大比重,显示总体各单位向中心值集中。所以集中趋势的测定指标是反映总体各

单位变量分布的一般水平的代表性指标。如要了解某个行业的劳动生产率水平,既不能用该行业最高的 劳动生产幸来表示,也不能用最低的劳动生产率来表示,而应该用行业的一般劳动生产率即平均劳动生 产率来反映整个行业劳动生产率的整体水平 2比较同类现 在不同单位的发展水平 比不同单位同类现象的发展水平, 般不能用总量指标来对比,因为总量指标会受到规模大小差 异的影响,不能简单加以比较。例如评价两个同行业企业的职工工资水平,即不能用每一个职工的工资 一一比较,也不能用工资总额指标来对比,因为工资总额会因企业职工人数的差异而不同,如果用平均 工资进行比较,就可以比较客观地说明间顺。因此,集中趋势在说明生产水平、消费水平、经济效益或 工作质量等方面、以及投资项目评估、生产消耗定额的制定、产品成本核算等许多场合都被广泛应用。 3,比较同类现象在不同时期的发展变化趋势或规律 社会经济现象的变化受多种因素的影响,个别单位或标志总量的变化,除了受现象规模的影响外 还易受偶然因素的影响。测定集中趋势,既可以避免受现象规模的影响,又能够消除偶然因素的作用, 比较确切地反映意体现象变化的基本趋势。例如研究居民收入水平的变动情况,个别居民的收入有特联 生,不足以反映 一般水平的变化,而居民总收入的变动又受居民人数变化的影响。如果采用各年居民的 平均收入水平进行比较 则可以反映出居民收入水平的变动趋势。 4.分析现象之间的依存关系 相互联系的客观现象的依存关系,不能取现象的某个具体值,而必须采纳其代表值。例如,将工业 企业按照规模的大小进行分组,再计算各不同规摸工业企业的劳动生产率、利润率等指标,就可以反映 出企业却的不同与劳动生产率利润率之间的关系 下面根据集中趋势各种测定指标所适用的数据等级,从初级到高级,即从位置代表值到数值代表值 分别予以介绍。我们特别需要注意的是,低层次数据的测定值适用于高层次数据的测量,但是高层次的 测定值并不适用于低层次数据的测定。 3.1.2位置平均数 位置平均数是根据数据排列位置所确定的代表值,其与数值平均数的基本区别在于不需要依据每 个数据值来计算。常用的位置代表值有众数和中位数,以及中位数之外的其它分位数。 1.众数(Mode) 众数是总体中出现次数最多的那个数据值,在须数分布中,众数指频数或颊率最大的标志值,用 M0表示。从数据的分布层面看,分布数列中最常出现的标志值说明该标志值最具有代表性,因此可以 反映数列的 一般才 在分配曲线图上,众数就是曲线的最高峰所对应的标志值 但是,众数具有不确定性。如果数据的分布没有明显的集中趋势或最高峰点,众数就不存在:如果 有多个高峰点,就有多众数。见图31众数示意图。 于个 (a)单众数 (b)双众 (c)五种无众数的情形 图3-1众数示意图 众数是英国统计学家皮尔生(Karl Pearson,1857~l936)首先提出来的,它对数据等级的要求是所
2 单位变量分布的一般水平的代表性指标。如要了解某个行业的劳动生产率水平,既不能用该行业最高的 劳动生产率来表示,也不能用最低的劳动生产率来表示,而应该用行业的一般劳动生产率即平均劳动生 产率来反映整个行业劳动生产率的整体水平。 2.比较同类现象在不同单位的发展水平 比较不同单位同类现象的发展水平,一般不能用总量指标来对比,因为总量指标会受到规模大小差 异的影响,不能简单加以比较。例如评价两个同行业企业的职工工资水平,即不能用每一个职工的工资 一一比较,也不能用工资总额指标来对比,因为工资总额会因企业职工人数的差异而不同,如果用平均 工资进行比较,就可以比较客观地说明问题。因此,集中趋势在说明生产水平、消费水平、经济效益或 工作质量等方面、以及投资项目评估、生产消耗定额的制定、产品成本核算等许多场合都被广泛应用。 3.比较同类现象在不同时期的发展变化趋势或规律 社会经济现象的变化受多种因素的影响,个别单位或标志总量的变化,除了受现象规模的影响外, 还易受偶然因素的影响。测定集中趋势,既可以避免受现象规模的影响,又能够消除偶然因素的作用, 比较确切地反映总体现象变化的基本趋势。例如研究居民收入水平的变动情况,个别居民的收入有特殊 性,不足以反映一般水平的变化,而居民总收入的变动又受居民人数变化的影响。如果采用各年居民的 平均收入水平进行比较,则可以反映出居民收入水平的变动趋势。 4.分析现象之间的依存关系 相互联系的客观现象的依存关系,不能取现象的某个具体值,而必须采纳其代表值。例如,将工业 企业按照规模的大小进行分组,再计算各不同规模工业企业的劳动生产率、利润率等指标,就可以反映 出企业规模的不同与劳动生产率或利润率之间的关系。 下面根据集中趋势各种测定指标所适用的数据等级, 从初级到高级, 即从位置代表值到数值代表值, 分别予以介绍。我们特别需要注意的是,低层次数据的测定值适用于高层次数据的测量,但是高层次的 测定值并不适用于低层次数据的测定。 3.1.2 位置平均数 位置平均数是根据数据排列位置所确定的代表值,其与数值平均数的基本区别在于不需要依据每一 个数据值来计算。常用的位置代表值有众数和中位数,以及中位数之外的其它分位数。 1.众数(Mode) 众数是总体中出现次数最多的那个数据值,在频数分布中,众数指频数或频率最大的标志值,用 Mo 表示。从数据的分布层面看,分布数列中最常出现的标志值说明该标志值最具有代表性,因此可以 反映数列的一般水平。 在分配曲线图上,众数就是曲线的最高峰所对应的标志值。 但是,众数具有不确定性。如果数据的分布没有明显的集中趋势或最高峰点,众数就不存在;如果 有多个高峰点,就有多众数。见图 3-1 众数示意图。 Mo Mo Mo 无众数 (a)单众数 (b)双众数 (c)五种无众数的情形 图 3-1 众数示意图 众数是英国统计学家皮尔生(Karl Pearson,1857~1936)首先提出来的,它对数据等级的要求是所

有集中趋势的代表值中最低的,从定类尺度开始的四种计量尺度测定的数据都适用。由于众数的特性, 实践中有时就利用它来表明现象的一般水平,有时利用它来作为某些决策的参考依据。如服装厂在制订 各种型号服装的生产计划时,计划产量最多的型号就是市场上销售量最大的型号。再如,在选举中,获 得最多票数者当选其实就是众数的应用。 众数一般用于总体数据。由于未 整理的数据不知道哪个标志值出现次数最多 就无法确定众数 因此,为了确定众数,必须先将资料进行分组,编制分配数列。又由于数量变量的分组有单项式分组和 组距式分组,而组距式分组又有等距分组和不等距分组之分,因此,各种不同的数据条件确定众数的方 法又有所不同。 (1)品质数列和单项式数量数列确定众数 由品质数列和单项式数量分配数列确定众数,方法比较简单。即出现次数最多的标志值就是众数 [例3-1】2000年福建省城镇居民家庭居住条件构成如表3-1。 表3-1 城镇居民家庭居住条件构成 (%) 项 2000年 按房屋产权分 100.0 租赁私房 12.6 1.9 自有房 71.7 其他 13.8 资料来源:《福建统计年鉴一2002》. 按房屋产权分组数据就是一个品质数列,有71.7%的城镇居民的住房是自有房,因为71.7%是该品质 数列中的最高频率,因此,其众数就是“自有房”,=自有房。 [例3-2】某学院某学年教师开课门数如表3-2: 表3-2教师开课门数(单位:门) 开课门数x 2 3 4 合计 教师数f 15 3028 12 85 在上表的单项式数量数列中,教师开课门数最集中的是2门课,所以2就是众数,M2。 (②)由组距数量数列确定众数 由组距数列确定众数,首先应当确定众数组,然后通过比例插值法计算众数。在等距分组条件下, 众数组就是次数最多的那一组:在不等距分组的条件下,众数组则是频数密度或频率密度最高的那一组 众数值是依据众数组的次数与众数组相邻的两组次数的关系用比例插值计算的。 图3-2表达了比例插值法的思路
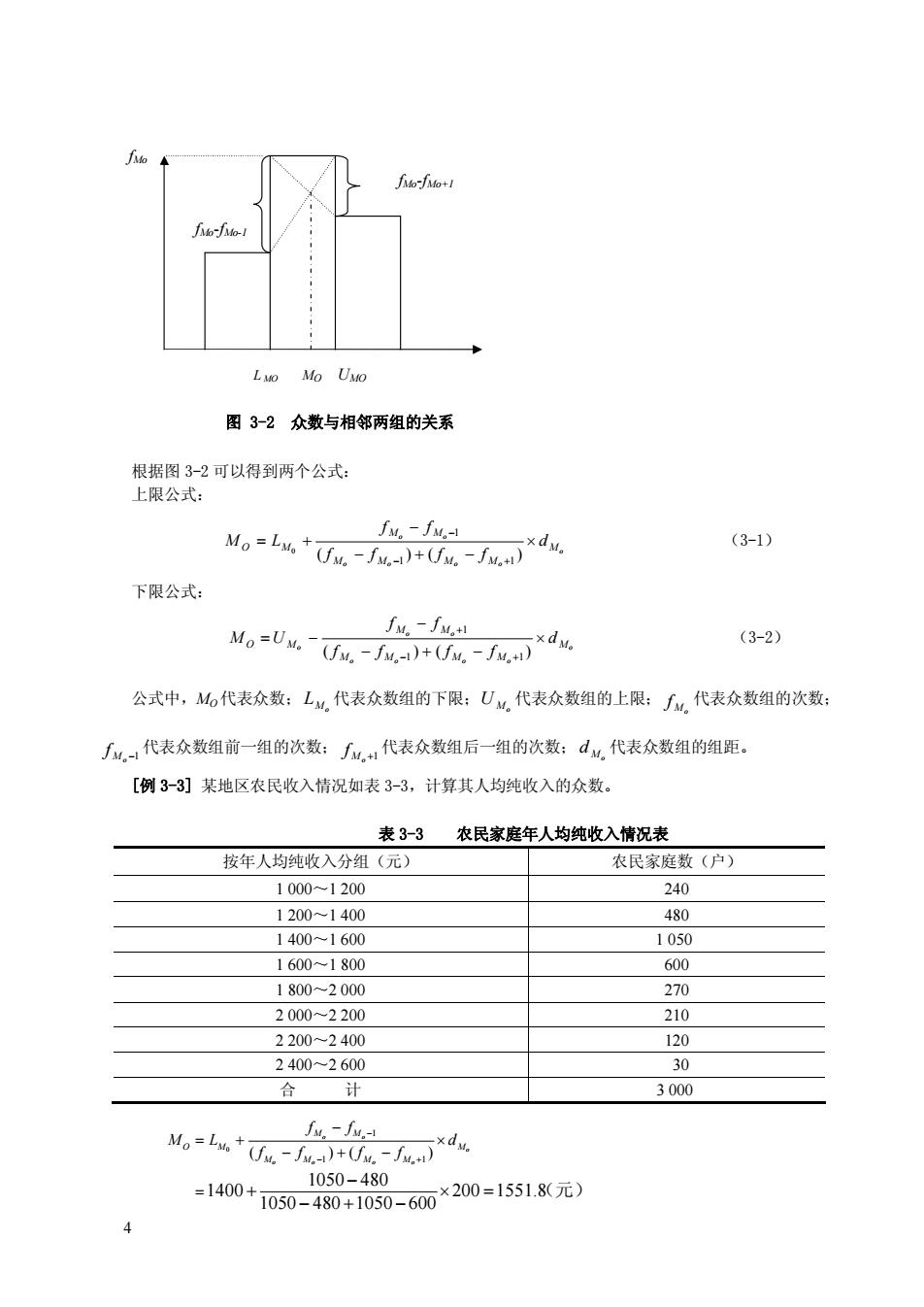
3 有集中趋势的代表值中最低的,从定类尺度开始的四种计量尺度测定的数据都适用。由于众数的特性, 实践中有时就利用它来表明现象的一般水平,有时利用它来作为某些决策的参考依据。如服装厂在制订 各种型号服装的生产计划时,计划产量最多的型号就是市场上销售量最大的型号。再如,在选举中,获 得最多票数者当选其实就是众数的应用。 众数一般用于总体数据。由于未经整理的数据不知道哪个标志值出现次数最多,就无法确定众数。 因此,为了确定众数,必须先将资料进行分组,编制分配数列。又由于数量变量的分组有单项式分组和 组距式分组,而组距式分组又有等距分组和不等距分组之分,因此,各种不同的数据条件确定众数的方 法又有所不同。 (1)品质数列和单项式数量数列确定众数 由品质数列和单项式数量分配数列确定众数,方法比较简单。即出现次数最多的标志值就是众数。 [例 3-1] 2000 年福建省城镇居民家庭居住条件构成如表 3-1。 表 3-1 城镇居民家庭居住条件构成 (%) 资料来源:《福建统计年鉴—2002》。 按房屋产权分组数据就是一个品质数列, 有 71.7%的城镇居民的住房是自有房, 因为 71.7%是该品质 数列中的最高频率,因此,其众数就是“自有房” ,MO=自有房。 [例 3-2] 某学院某学年教师开课门数如表 3-2: 表 3-2 教师开课门数 (单位:门) 开课门数 x 1 2 3 4 合计 教师数 f 15 30 28 12 85 在上表的单项式数量数列中,教师开课门数最集中的是 2 门课,所以 2 就是众数,MO=2。 (2)由组距数量数列确定众数 由组距数列确定众数,首先应当确定众数组,然后通过比例插值法计算众数。在等距分组条件下, 众数组就是次数最多的那一组; 在不等距分组的条件下, 众数组则是频数密度或频率密度最高的那一组。 众数值是依据众数组的次数与众数组相邻的两组次数的关系用比例插值计算的。 图 3-2 表达了比例插值法的思路。 项 目 2000 年 按房屋产权分 100.0 公 房 12.6 租赁私房 1.9 自 有 房 71.7 其 他 13.8
LM0 Mo UMo 图32众数与相邻两组的关系 根据图3-2可以得到两个公式 上限公式: Mou (fw.a)dv. JM。-JM。-1 (3-1) 下限公式: 。=Uu.-fa+-fn*dw (3-2) 公式中,M6代表众数:LM,代表众数组的下限:UM,代表众数组的上限:了代表众数组的次数 ∫,一代表众数组前一组的次数:∫4,代表众数组后一组的次数:d代表众数组的组距。 [例3-3]某地区农民收入情况如表3-3,计算其人均纯收入的众数。 表3-3农民家庭年人均纯收入情况表 按年人均纯收入分组(元) 农民家庭数(户) 1000-1200 240 12001400 480 14001600 1050 1600~1800 600 1800-2000 270 2000-2200 210 2200~2400 120 2400-2600 30 3000 fy -fu- M。=L+-+-*4u 480+1050-600×200=1551.8元) 1050-480 =1400- 1050
4 fMo fMofMo+1 fMofMo1 L MO MO UMO 图 3-2 众数与相邻两组的关系 根据图 3-2 可以得到两个公式: 上限公式: o o o o o o o M M M M M M M O M d f f f f f f M L ¥ - + - - = + - + - ( ) ( ) 1 1 1 0 (3-1) 下限公式: o o o o o o o o M M M M M M M O M d f f f f f f M U ¥ - + - - = - - + + ( ) ( ) 1 1 1 (3-2) 公式中,MO 代表众数; M o L 代表众数组的下限; M o U 代表众数组的上限; M o f 代表众数组的次数; -1 M o f 代表众数组前一组的次数; +1 M o f 代表众数组后一组的次数; M o d 代表众数组的组距。 [例 3-3] 某地区农民收入情况如表 3-3,计算其人均纯收入的众数。 表 3-3 农民家庭年人均纯收入情况表 按年人均纯收入分组(元) 农民家庭数(户) 1 000~1 200 240 1 200~1 400 480 1 400~1 600 1 050 1 600~1 800 600 1 800~2 000 270 2 000~2 200 210 2 200~2 400 120 2 400~2 600 30 合 计 3 000 0 1 1 1 ( ) ( ) 1050 480 1400 200 1551.8 1050 480 1050 600 o o o o o o o M M O M M M M M M f f M L d f f f f - - + - = + ¥ - + - = - + ¥ = - + - (元)

或: fy.-fu 。=-+-x4 1600- 1050 050-480)+0050-600×200=1518元) 在不等距分组的条件下,众数必须根据频数密度或频率密度来计算。 众数是按照数据的位置计算的,它的长处是易于理解,不受极端数值的影响。当数据分布存在明显 的集中趋势,且有显著的极端值时,适合使用众数。但是其灵敏度、计算功能和稳定性差,具有不唯 性,所以当数据分布 中趋势不明显或存在两个以上分布中心时,便不适合使用众数(前者无众数 后者为双众数或多众数,也等于没有众数)。 2.中位数(Median) 中位数和众数一样,也是一种位置代表值,但是,它不能用于定类数据,只能在顺序及以上的数据 中使用,所以又称为次序统计量,用Me表示。 中位数是将总体中的数据按顺序排列后,处于数列中点位置上的那个数据值或变量值,或者说中位 数是累计频率数列中 累 为0.50 的变 从中位数概念可见:在总体中,小于中位数的数据个数占一半,大于中位数的数据个数也占一半 即中位数是将数据按大小顺序排列后,位于二等分点上的那个数据值。用中位数来代表总体中所有标志 值的一般水平,可以避免极端值的影响,在有的情况下更具有代表性。例如,人口的平均年龄会受到个 别特别长寿人口年龄的影响,使计算结果偏大,而年龄中位数则可以较好地体现人口年龄结构的特征: 国际上就使用人口的年龄中位数(30岁)作为人口老龄化的一个判断标准。 中位数的确定方法,根据所掌握的数据不同而有所不同 (1)由顺序数据和未分组的数量数据确定中位数。这种情况下,确定中位数的方法是:先将总体 中的全部数据顺序排列,然后确定中位数的位置,处于中位数位置的标志值就是中位数。 顺序数据中位数的位置: 中位数位置=号 (3-3) 未分组的数量数据中位数的位置: 中位数位置=”+1 (3-4) 式中,n为数据个数。 当数据个数刀为奇数时,中位数是处于中间位置上的数据值 当数据个数n为偶数时,中位数是处于中间位置上的两个数据值的算术平均数。 M,=x时 (3.5) M,=+) (3-6) [例3-4)某高校一次对食堂伙食满意度的调查数据如表3-4所示。 表3-4 调查数据次数分布 回答类别 学生人数(人) 学生数累计(向上累计) 非常不满意 240 240 不满意 1080 1320 930 2250 一意 450 2700
5 或: 1 1 1 ( ) ( ) 1600 1050 600 200 1551.8 (1050 480) (1050 600) o o o o o o o o M M O M M M M M M f f M U d f f f f + - + - = - ¥ - + - = - - ¥ = - + - (元) 在不等距分组的条件下,众数必须根据频数密度或频率密度来计算。 众数是按照数据的位置计算的,它的长处是易于理解,不受极端数值的影响。当数据分布存在明显 的集中趋势,且有显著的极端值时,适合使用众数。但是其灵敏度、计算功能和稳定性差,具有不唯一 性,所以当数据分布的集中趋势不明显或存在两个以上分布中心时,便不适合使用众数(前者无众数, 后者为双众数或多众数,也等于没有众数)。 2.中位数(Median) 中位数和众数一样,也是一种位置代表值,但是,它不能用于定类数据,只能在顺序及以上的数据 中使用,所以又称为次序统计量,用 Me 表示。 中位数是将总体中的数据按顺序排列后,处于数列中点位置上的那个数据值或变量值,或者说中位 数是累计频率数列中,累计频率为 0.50 所对应的变量值。 从中位数概念可见:在总体中,小于中位数的数据个数占一半,大于中位数的数据个数也占一半, 即中位数是将数据按大小顺序排列后,位于二等分点上的那个数据值。用中位数来代表总体中所有标志 值的一般水平,可以避免极端值的影响,在有的情况下更具有代表性。例如,人口的平均年龄会受到个 别特别长寿人口年龄的影响,使计算结果偏大,而年龄中位数则可以较好地体现人口年龄结构的特征, 国际上就使用人口的年龄中位数(30 岁)作为人口老龄化的一个判断标准。 中位数的确定方法,根据所掌握的数据不同而有所不同: (1)由顺序数据和未分组的数量数据确定中位数。这种情况下,确定中位数的方法是:先将总体 中的全部数据顺序排列,然后确定中位数的位置,处于中位数位置的标志值就是中位数。 顺序数据中位数的位置: 中位数位置= 2 n (3-3) 未分组的数量数据中位数的位置: 中位数位置= 2 n +1 (3-4) 式中,n 为数据个数。 当数据个数 n 为奇数时,中位数是处于中间位置上的数据值。 当数据个数 n 为偶数时,中位数是处于中间位置上的两个数据值的算术平均数。 1 2 Me n x = + (35) 1 2 2 1 ( ) 2 Me n n x x + = + (3-6) [例 3-4] 某高校一次对食堂伙食满意度的调查数据如表 3-4 所示。 表 3-4 调查数据次数分布 回答类别 学生人数(人) 学生数累计(向上累计) 非常不满意 240 240 不满意 1 080 1 320 一 般 930 2 250 满 意 450 2 700