连通和DFS ■如何判定两个顶点是否连通? ■ 如何判定一个图是否连通? VI e es VA 2023/2/27 21
n 如何判定两个顶点是否连通? n 如何判定一个图是否连通? 2023/2/27 21 连通和DFS v1 v2 v3 v4 e1 e2 e4

连通和DFS ■深度优先搜索(DFS)算法 ·从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 ●遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 N 算法2.1:DFS Vs e e3 输人:图G=(V,E),顶点u 初值:V中所有顶点的visited初值为false e6 1u.visited←-true; 2 foreach(u,v)∈Edo e2 N ea 3 if v.visited false then 4 DFS(G,v); es V3 2023/2/27 22
n 深度优先搜索(DFS)算法 l 从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 l 遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 2023/2/27 22 连通和DFS
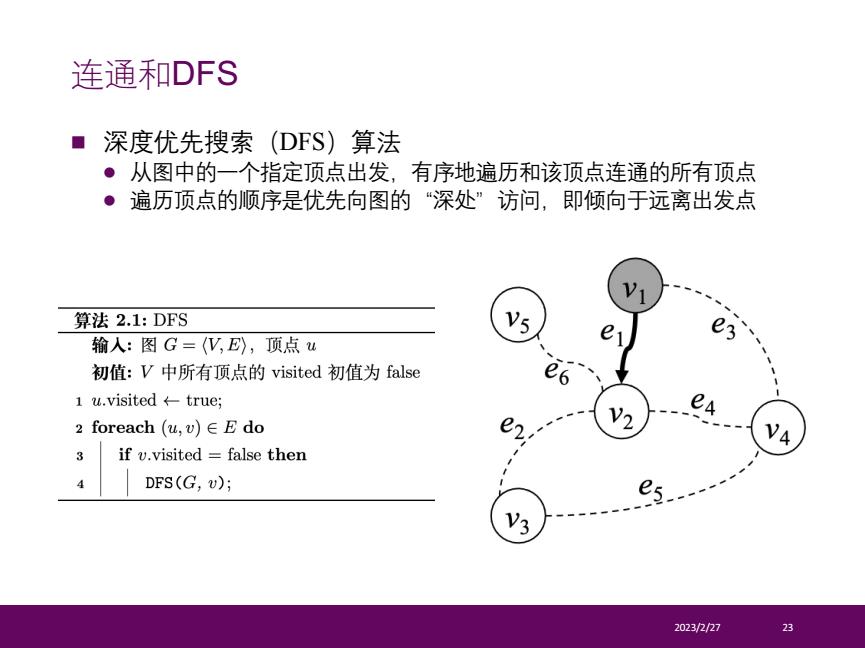
连通和DFS ■深度优先搜索(DFS)算法 ·从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 ●遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 算法2.1:DFS e 输人:图G=(V,E),顶点u e3 初值:V中所有顶点的visited初值为false 1u.visited←-true; 2 foreach(u,v)∈Edo e 3 if v.visited false then 4 DFS(G,v); es 2023/2/27 23
n 深度优先搜索(DFS)算法 l 从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 l 遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 2023/2/27 23 连通和DFS
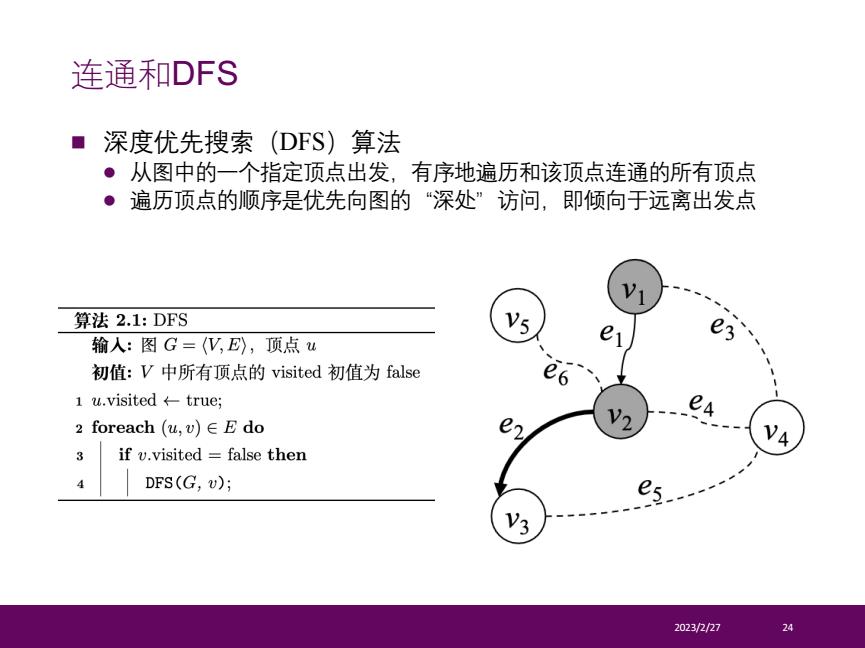
连通和DFS ■深度优先搜索(DFS)算法 ·从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 ●遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 算法2.1:DFS Vs e 输人:图G=(V,E),顶点u e 初值:V中所有顶点的visited初值为false e6 1u.visited←-true; 2 foreach(u,v)∈Edo e N 3 if v.visited false then DFS(G,v); 2023/2/27 24
n 深度优先搜索(DFS)算法 l 从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 l 遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 2023/2/27 24 连通和DFS
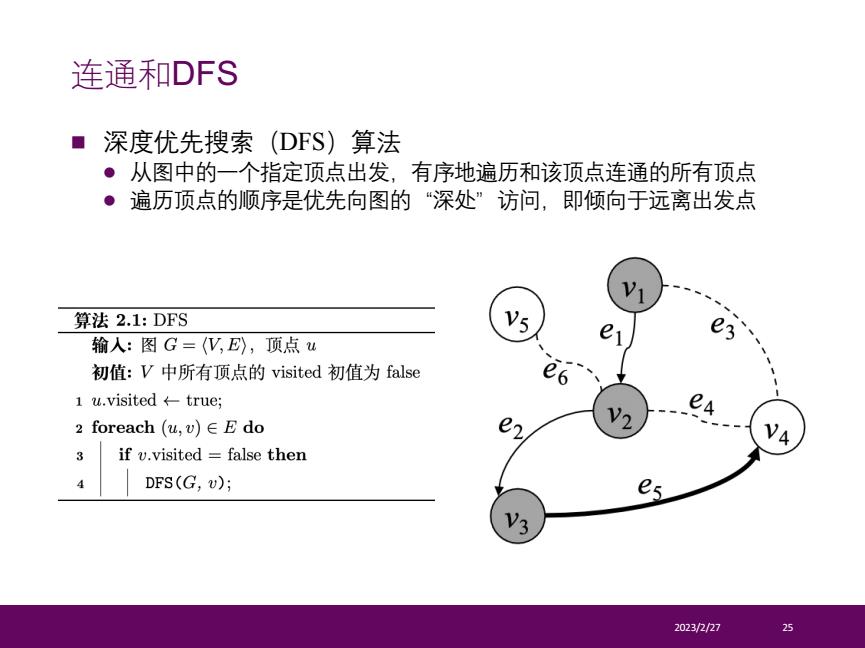
连通和DFS ■深度优先搜索(DFS)算法 ·从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 ●遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 算法2.1:DFS es 输人:图G=(V,E),顶点u e 初值:V中所有顶点的visited初值为false 1u.visited←-true; eA 2 foreach(u,v)∈Edo e 3 if v.visited false then 4 DFS(G,v); es N3 2023/2/27 25
n 深度优先搜索(DFS)算法 l 从图中的一个指定顶点出发,有序地遍历和该顶点连通的所有顶点 l 遍历顶点的顺序是优先向图的“深处”访问,即倾向于远离出发点 2023/2/27 25 连通和DFS