
电工技术 星形 三角形 dlangong R RR+RR+R3R R31 R R12 RR,+RR+RR R2 R R3 R23 R2 R31= RR2+RR3+R3R R 特点: 当R1=R2=R3=Rv时,有: R2=R23=R31=R=3Ry 上一页下一页
上一页 下一页 (2 17) 2 1 2 2 3 3 1 3 1 1 1 2 2 3 3 1 2 3 3 1 2 2 3 3 1 1 2 − + + = + + = + + = R R R R R R R R R R R R R R R R R R R R R R R R 星形 三角形 特点: 当R1 = R2 = R3 = RY时,有: 3 (2 19) R12 = R23 = R31 = R = R − R31 R12 R23 R1 R R2 3
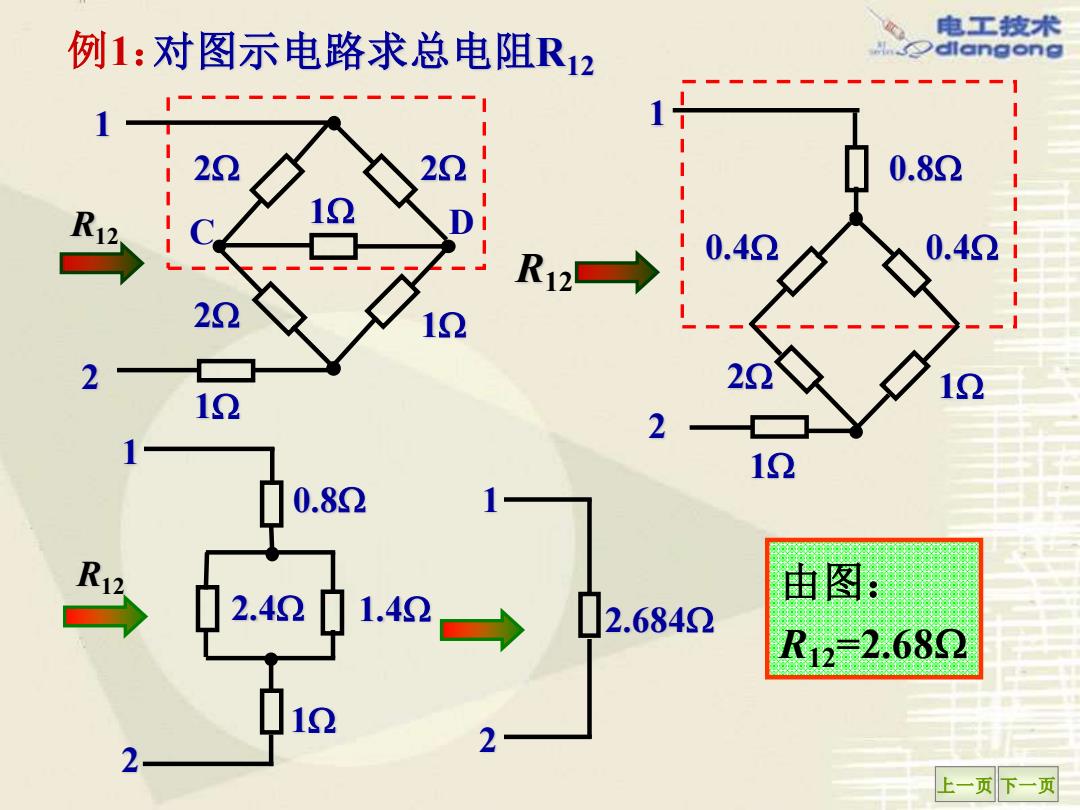
电工技术 例1:对图示电路求总电阻R12 dlangong 0.82 0.42 .4Ω 22 12 12 0.82 12.42 由图 .42 2.6842 R12=2.682 2 上一页下一页
上一页 下一页 例1:对图示电路求总电阻R12 R12 2 1 2 2 2 1 1 1 由图: R12=2.68 R12 C D 1 2 1 1 0.4 0.4 0.8 2 R12 1 0.8 2.4 1.4 1 2 1 2 2.684

电工技术 例2:计算下图电路中的电流11。 dlangong a 8 12V 12V 解:将联成△形abc的电阻变换为Y形联结的等效电阻 4×8 2= Rap Rca 0=22 Ran+Rpe+Rca 4+4+8 4×4 2=10 8×4 0=22 4+4+8 R= 4+4+8 上一页下一页
上一页 下一页 例2:计算下图电路中的电流 I1 。 I1 + – 4 5 8 4 4 12V a b d c 解:将联成形abc的电阻变换为Y形联结的等效电阻 I1 + – 4 5 Ra Rb Rc 12V a b c d Ω 2 Ω 4 4 8 4 8 a b bc ca a b ca a = + + = + + = R R R R R R Ω 1Ω 4 4 8 4 4 b = + + R = Ω 2 Ω 4 4 8 8 4 c = + + R =
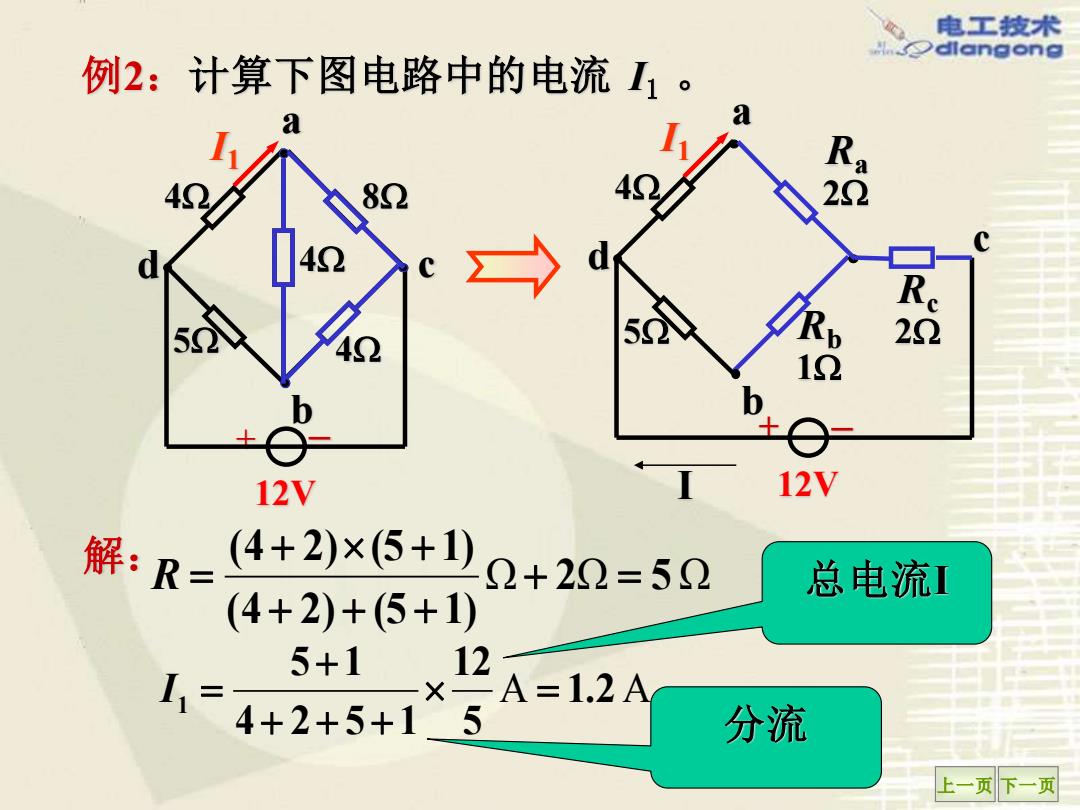
电工技术 dlangong 例2:计算下图电路中的电流1。 a 22 12 12V 12V 解:R=4+2列x5+1少0+20=5Q 总电流缸 (4+2)+(5+1) 5+1 1,=4+2+5+1 2A=1.2A 分流 上一页下一页
上一页 下一页 例2:计算下图电路中的电流 I1 。 I1 + – 4 5 8 4 4 12V a b d c 解: I1 + – 4 5 Ra 2 Rb 1 Rc 2 12V a b c d Ω 2Ω 5 Ω (4 2) (5 1) (4 2) (5 1) + = + + + + + R = A 1.2 A 5 12 4 2 5 1 5 1 1 = + + + + I = 总电流I I 分流

上一页 下一页