
第三章:感知景 3.1单个感知器模型与解决问题的能力 连续感知器(简称感知器) 连续感知器人工神经元结构及其数学描述如下: 激活函数:y=f(o)=k0+b 7+ n+ W:2 y=f(∑wx)=k∑wx+b i- 若取k=1,b=0 ,则其成为一类最简单的连续人工感知神经元
连续感知器(简称感知器) 第三章:感知器 3.1 单个感知器模型与解决问题的能力 y f w x k w x b n i i i n i = i i = + + = + = 1 1 1 1 ( ) 连续感知器人工神经元结构及其数学描述如下: 若取 k =1,b = 0 ,则其成为一类最简单的连续人工感知神经元。 激活函数: y f o k o b = = + ( )

第三章:感知恐 31单个感知器模型与解决问题的能力 定义:a)如果x的每个向量x都在{0,1或{-1,1}上取值, 且激活涵函数f(x)=sgn(x)是不连续的: 1x≥0 或0 x≥0 x<0 那么这个感知神经元被成为M-P模型。 b)如果x”∈R”但激励函数f(x)是离散的,那么这个 感知神经元被称为离散感知器 一常简称为感知器。 C)如果x”∈R”且f(x)是连续函数,那么这个感知 神经元称为连续感知器。 由相应的感知神经元组成的网络就称为相应神经网络,如 M-P神经网络、感知器神经网络、连续感知器神经网络
第三章:感知器 3.1 单个感知器模型与解决问题的能力 n x i x 是不连续的: 或 − = 1 0 1 0 ( ) x x f x = 0 0 1 0 ( ) x x f x 定义: 的每个向量 都在{0,1}或{-1,1}上取值, f (x) = sgn( x) a)如果 且激活函数 那么这个感知神经元被成为M-P模型。 b) 如果 x n , R n 但激励函数 f (x) 是离散的,那么这个 感知神经元被称为离散感知器——常简称为感知器。 是连续函数,那么这个感知 n n C) 如果 x R 且 f (x) 神经元称为连续感知器。 由相应的感知神经元组成的网络就称为相应神经网络,如 M-P神经网络、感知器神经网络、连续感知器神经网络
第三章:感知聚 3.1单个感知器模型与解决问题的能力 例线性不可分集合。 二维平面上的两类模式一异或(XO)问题,见表。 二维平面中不存在一条直线,将输入模式分为两类,此输入 模式称线性不可分集合,见图。 可见:单层感知器不能解决异或问题。 表2-3-3 2 0 0 0 0 1 1 0 1 图2-3-4 山 结论:单个感知霖不能对线性不可分门题实现两类分类
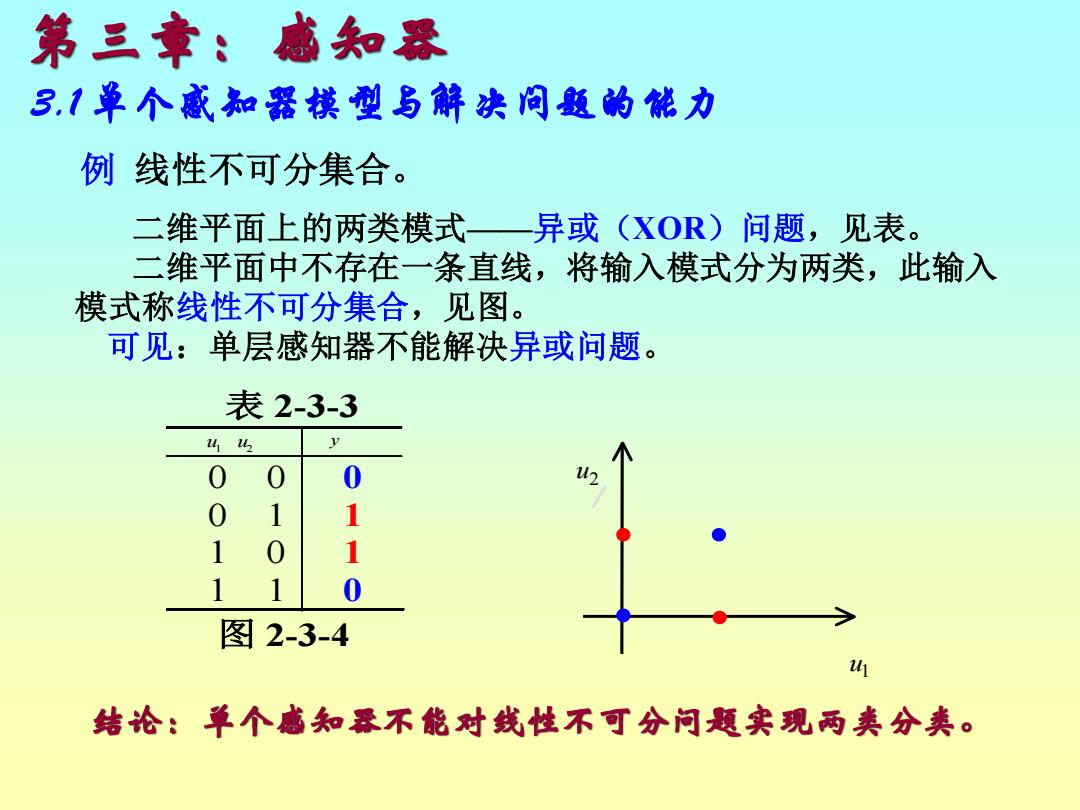
例 线性不可分集合。 二维平面上的两类模式——异或(XOR)问题,见表。 二维平面中不存在一条直线,将输入模式分为两类,此输入 模式称线性不可分集合,见图。 可见:单层感知器不能解决异或问题。 表 2-3-3 u1 u2 y 0 0 0 0 1 1 1 0 1 1 1 0 图 2-3-4 异或问题 u2 u1 第三章:感知器 3.1 单个感知器模型与解决问题的能力 结论:单个感知器不能对线性不可分问题实现两类分类
第三章:感知恐 3.1单个威知器模型与解决间题的能力 ·单层感知器工作原理 对于只有两个输入的判别边界是直线(如下式 所示),选择合适的学习算法可训练出满意的和, 当它用于两类模式的分类时,相当于在高维样本空 间中,用一个超平面将两类样本分开。 X2 类11 类12 判决边界 w1X1+w2x2+b=0
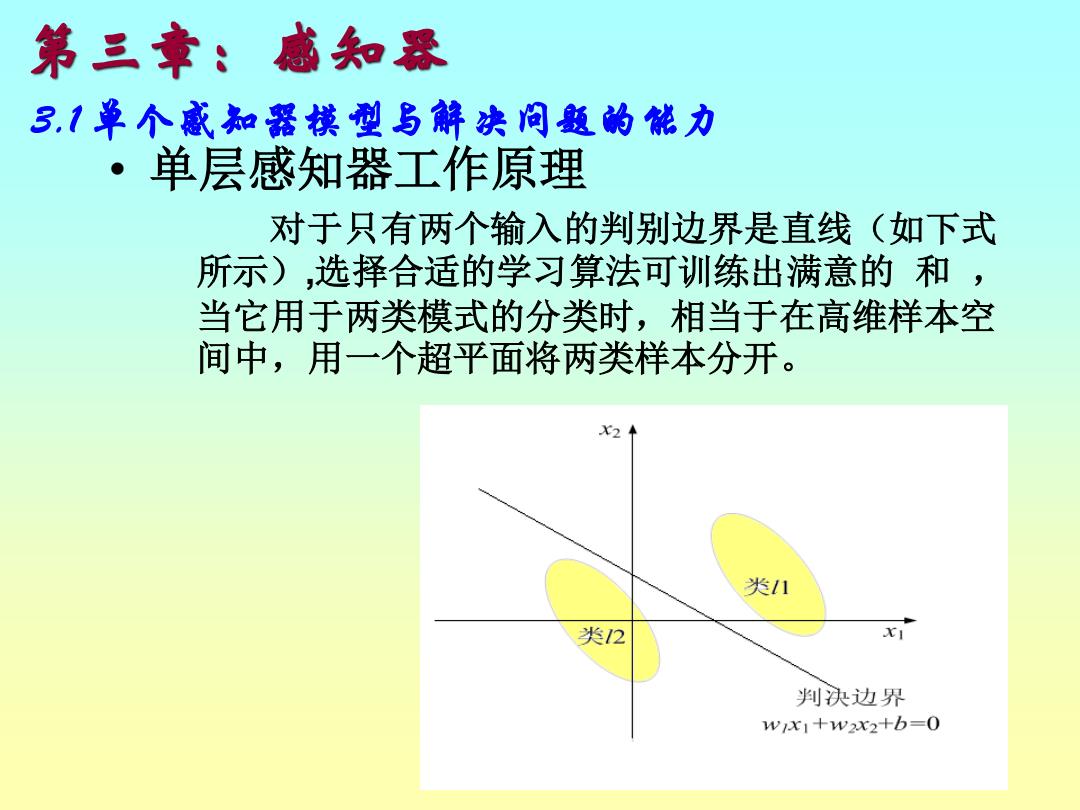
• 单层感知器工作原理 对于只有两个输入的判别边界是直线(如下式 所示),选择合适的学习算法可训练出满意的 和 , 当它用于两类模式的分类时,相当于在高维样本空 间中,用一个超平面将两类样本分开。 第三章:感知器 3.1 单个感知器模型与解决问题的能力
第三章:感知景 3.2单层感知器模型与解决问题的能力 在上一节中指出了线性单个感知神经网络只能实现两类 分类,如果要进行多于两类的分类将怎么办?生物医学已经 证明:生物神经系统是由一些相互联系的,并能互相传递信 息、的神经细胞互连构成。因此这就使我们自然地想到是否可 将单个的感知神经元连成网络形成一个单层的网络? 结构 X X2
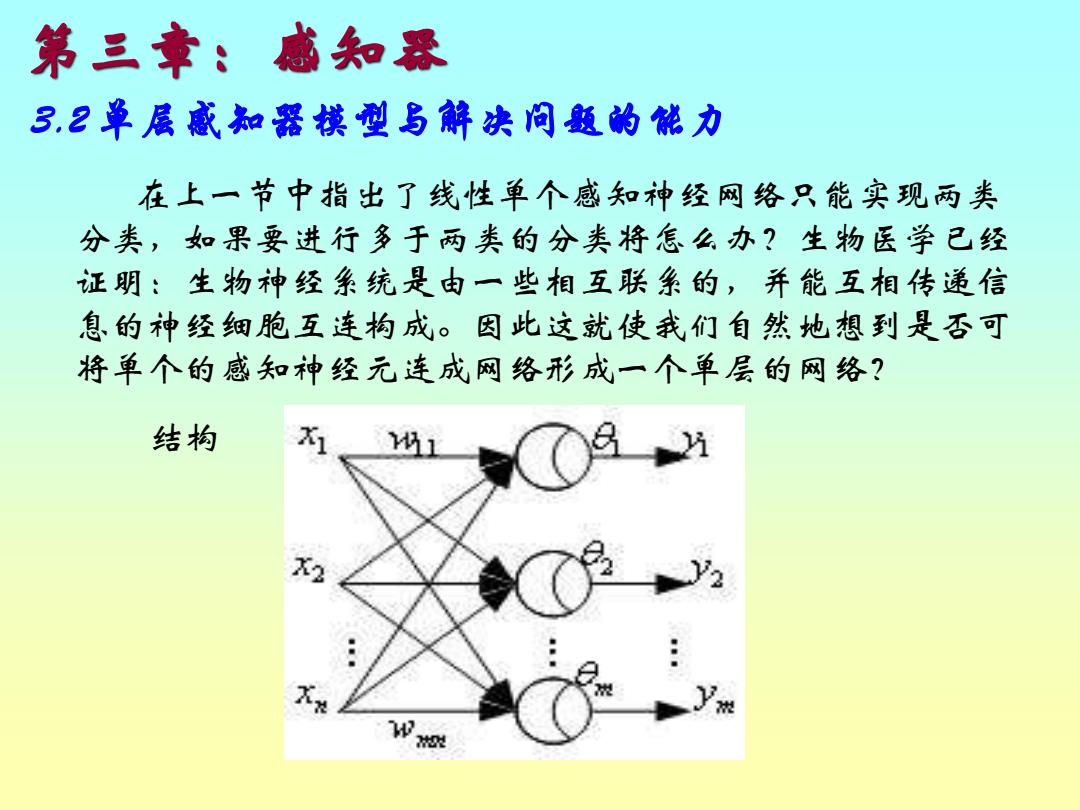
第三章:感知器 3.2 单层感知器模型与解决问题的能力 在上一节中指出了线性单个感知神经网络只能实现两类 分类,如果要进行多于两类的分类将怎么办?生物医学已经 证明:生物神经系统是由一些相互联系的,并能互相传递信 息的神经细胞互连构成。因此这就使我们自然地想到是否可 将单个的感知神经元连成网络形成一个单层的网络? 结构