
第三章:感知恐 31单个感知器模型与解决问题的能力 对与(b) y=f(4x1+3x3-2x2-6) 2a
第三章:感知器 3.1 单个感知器模型与解决问题的能力 对与(b) − − + − − + − = = + − − 1 4 2 3 6 0 1 4 2 3 6 0 (4 3 2 6) 1 2 3 1 2 3 1 3 2 x x x x x x y f x x x
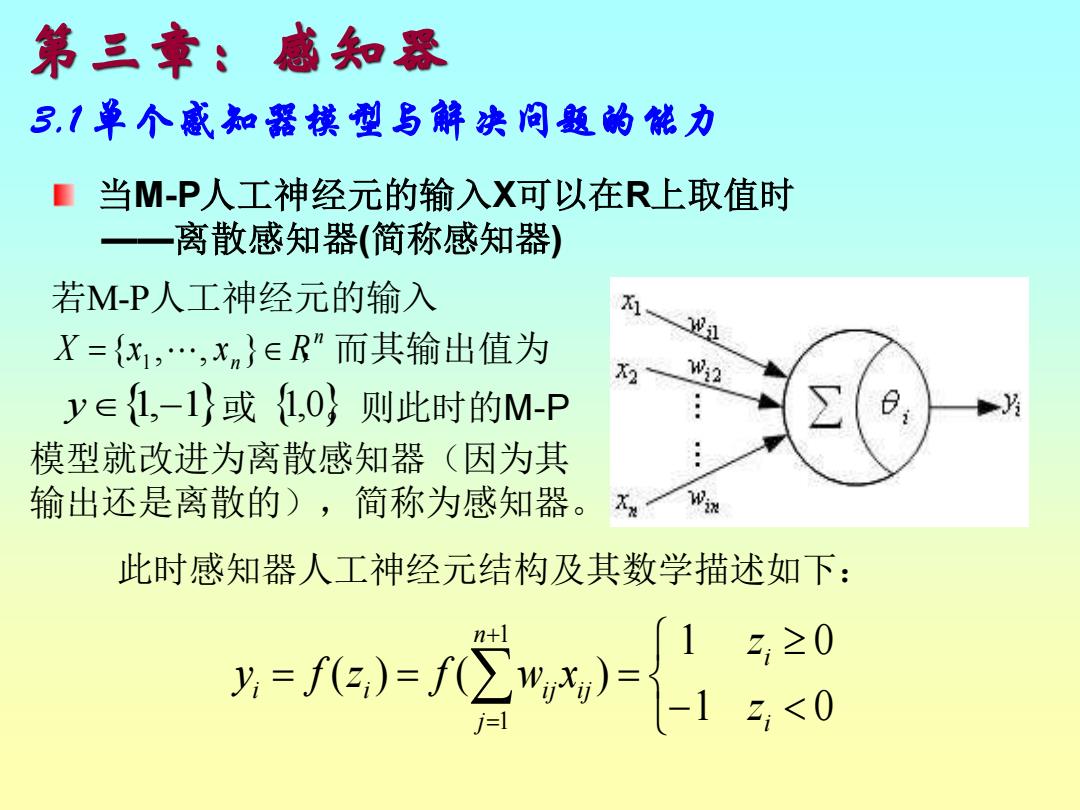
第三章:感知恐 3.1单个感知器模型与解决问题的能力 当M-P人工神经元的输入X可以在R上取值时 ——离散感知器(简称感知器) 若M-P人工神经元的输入 X={x,…,xn}∈R”而其输出值为 X2 00 y∈1,-1}或1,0}则此时的M-P 模型就改进为离散感知器(因为其 输出还是离散的),简称为感知器。x”w 此时感知器人工神经元结构及其数学描述如下:
第三章:感知器 3.1 单个感知器模型与解决问题的能力 此时感知器人工神经元结构及其数学描述如下: − = = = + = 1 0 1 0 ( ) ( ) 1 1 i i n j i i i j i j z z y f z f w x 当M-P人工神经元的输入X可以在R上取值时 ——离散感知器(简称感知器) n X = {x1 , , xn } R y1,−1 1,0 若M-P人工神经元的输入 ,而其输出值为 或 模型就改进为离散感知器(因为其 输出还是离散的),简称为感知器。 。则此时的M-P
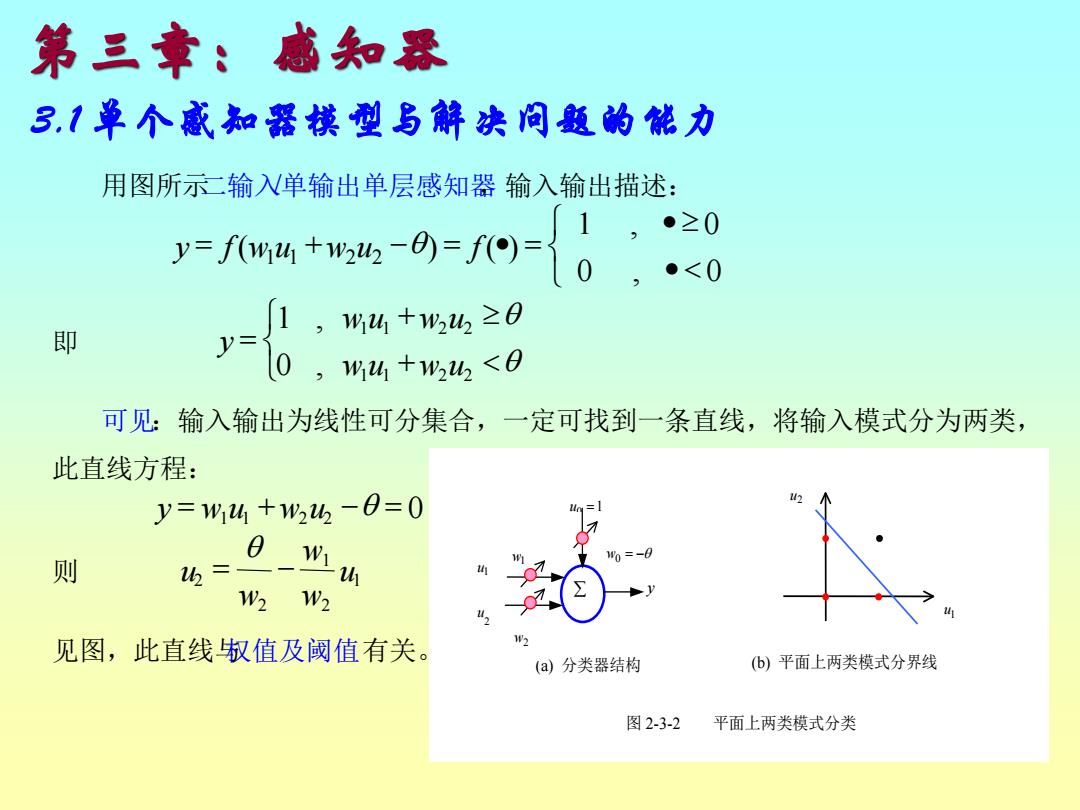
第三章:感知恐 3.1单个感知器模型与解决问题的能力 用图所示二输W单输出单层感知器输入输出描述: )=-=0-{0 ,·<0 即 6:w8 ),w4+2h2<0 可见输入输出为线性可分集合,一定可找到一条直线,将输入模式分为两类, 此直线方程: y=w14+w2h-8=0 则 0w1 W2 W2 见图,此直线叔值及阈值有关。 (a)分类器结构 (b)平面上两类模式分界线 图2-3-2 平面上两类模式分类
第三章:感知器 3.1 单个感知器模型与解决问题的能力 (a) 分类器结构 w2 w1 w0 = − y 1 u0 = 2 1 u u 1 u 2 u (b) 平面上两类模式分界线 图 2-3-2 平面上两类模式分类 用图所示二输入/单输出单层感知器,输入输出描述: • • = + − = • = 0 , 0 1 , 0 ( ) ( ) 1 1 2 2 y f wu w u f 即 + + = 1 1 2 2 1 1 2 2 0 , 1 , wu w u wu w u y 可见:输入输出为线性可分集合,一定可找到一条直线,将输入模式分为两类, 此直线方程: y = w u +w u − = 1 1 2 2 0 则 u w w w 2 u 2 1 2 1 = − 见图,此直线与权值及阈值有关
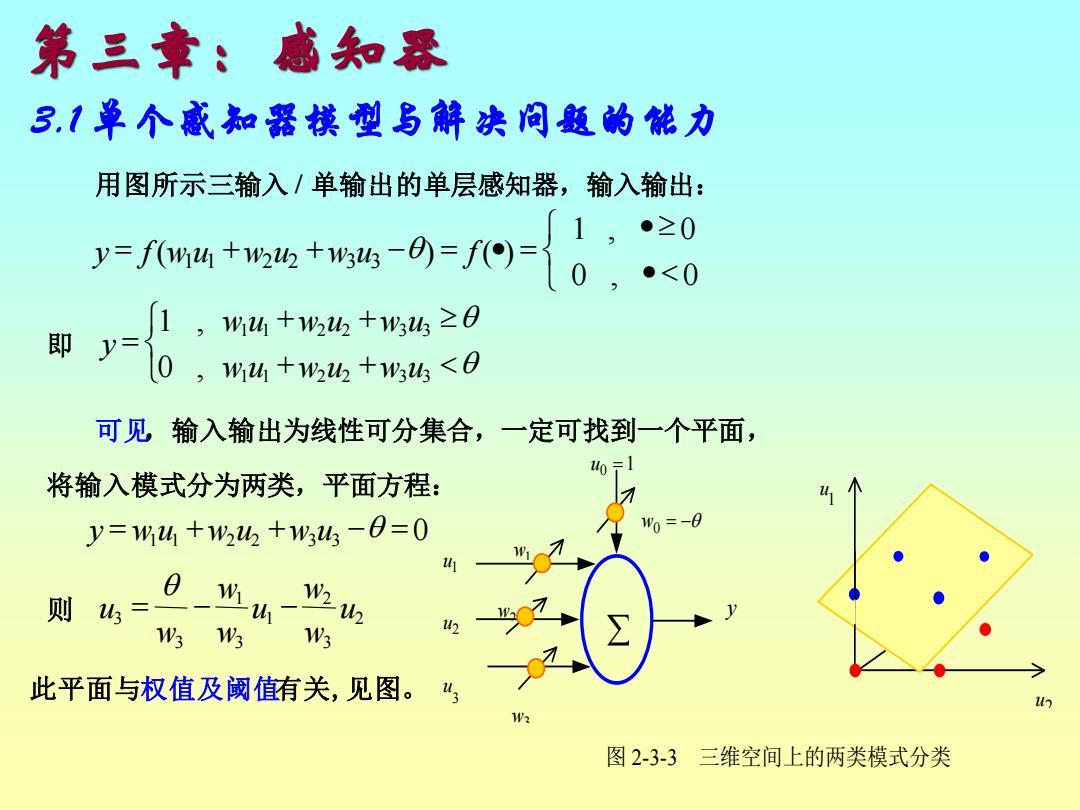
第三章:感知恐 31单个感知器模型与解决问题的能力 用图所示三输入/单输出的单层感知器,输入输出: m-4-9四{0:0 ●之0 7少=。:4十十6之 ),W4+w西+W3<B 可见输入输出为线性可分集合,一定可找到一个平面, 0=1 将输入模式分为两类,平面方程: y=%4+%2h+W4-8=0 1"0=-0 则4=6-山 W3 W3 此平面与权值及阈值有关,见图。“ 图2-3-3三维空间上的两类模式分类
第三章:感知器 3.1 单个感知器模型与解决问题的能力 2 u 1 u w0 = − 1 u0 = y w1 w3 w2 3 2 1 u u u 图 2-3-3 三维空间上的两类模式分类 用图所示三输入 / 单输出的单层感知器,输入输出: • • = + + − = • = 0 , 0 1 , 0 ( ) ( ) 1 1 2 2 3 3 y f wu w u w u f 即 + + + + = 1 1 2 2 3 3 1 1 2 2 3 3 0 , 1 , wu w u w u wu w u w u y 可见,输入输出为线性可分集合,一定可找到一个平面, 将输入模式分为两类,平面方程: y = w1u1 +w2u2 +w3u3 − = 0 则 2 3 2 1 3 1 3 3 u w w u w w w u = − − 此平面与权值及阈值有关,见图

第三章:感知恐 3.1单个感知器模型与解决问题的能力 感知器的分类定义 作为数学模型,我们对感知器作出如下归纳: 1感知器是一个多输入、单输出的运算系统,表示一个神经元 的运算特性,它的输入状态向量记为: x”=(x1x2…xn) 权向量: w”=(w11w2 ·…wn) 2.感知器的状态值可以为感知器的输出值 y=f(w”O,x") 3.以∑x-0=0为分界线,实现对输入的分类 y= 02x-0<0
第三章:感知器 3.1 单个感知器模型与解决问题的能力 感知器的分类定义 作为数学模型,我们对感知器作出如下归纳: 1.感知器是一个多输入、单输出的运算系统,表示一个神经元 的运算特性,它的输入状态向量记为: ( ) 1 2 n n x = x x x ( ) 1 2 n n 权向量: w = w w w 2. 感知器的状态值可以为感知器的输出值 ( ; ) n n y = f w x − − = = = 0 0 1 0 1 1 n i i i n i i i x x y 3. 以 x − = 0 为分界线,实现对输入的分类