
第二章定量资料的统计描述 一、基本概念 1.平均数用于反映一组观察值的平均水平,是描述计量资料集中趋势的指标。包括 算术均数、几何均数、中位数、众数及调和均数等。 2.变异指标反映一组观察值的离散趋势。常用者有极差、标准差、方差、四分位数 间距及变异系数等。 二、公式及应用条件 (一)算术均数用于正态分布或对称分布的资料 1.直接法x=∑xn 2.加权法x=∑x/∑f 3.简捷法x=x+(∑f/∑fD(i) (二)几何均数用于正偏态分布或对数正态分布资料。 1.直接法G=√X·X2.X。 G=lg'(∑lgx/n 2.加权法G=g(∑f1gx/∑f) (三)中位数应用条件:正负偏态资料:数据的一端或两端无确定数据:资料分布 不清。 1.直接法n为奇数M=Xa+☑ n为偶数M=X2a+2P 2.频数表法MeL+(i/fm)(n/2-c) (四)百分位数应用条件:①描述一组资料在某百分位置上的水平:②确定正常值 或参考值范围:③计算四分位数间距等。 公式Px=L+(if)(nxW100)-∑n) (五)众数M。一组观察值中出现次数最多的那个数值。在轻度偏态分布中,它与 X、M的关系为:M0-3M-2X (六)极差粗略估计一组观察值的变异大小。计算简便,但指标不太稳定。 R=最大值一最小值 (七)四分位数间距反映观察值中间1/2部分的变异,指标较为稳定。 Q=P5-P25=Q3-Q1 11
第二章 定量资料的统计描述 一、基本概念 1. 平均数 用于反映一组观察值的平均水平,是描述计量资料集中趋势的指标。包括 算术均数、几何均数、中位数、众数及调和均数等。 2. 变异指标 反映一组观察值的离散趋势。常用者有极差、标准差、方差、四分位数 间距及变异系数等。 二、公式及应用条件 (一)算术均数 用于正态分布或对称分布的资料 1. 直接法 x =∑xn 2. 加权法 x =∑fx/∑f 3. 简捷法 x =x0+(∑fx/∑f)(i) (二)几何均数 用于正偏态分布或对数正态分布资料。 1. 直接法 G X1 X 2 LLX n = ⋅ (∑ ) − G = lg lg x / n 1 2. 加权法 (∑ ∑ ) − G = lg f lg x / f 1 (三)中位数 应用条件:正负偏态资料;数据的一端或两端无确定数据;资料分布 不清。 1. 直接法 n为奇数 M=X[(n+1)/2] n为偶数 M=X[(n/2)+(n+1)/2]/2 2. 频数表法 M=L+(i/fm)(n/2 – c) (四)百分位数 应用条件:①描述一组资料在某百分位置上的水平;②确定正常值 或参考值范围;③计算四分位数间距等。 公式 PX=L+(i/fx)((n•x/100)-∑fL) (五)众数M。 一组观察值中出现次数最多的那个数值。在轻度偏态分布中,它与 X 、M的关系为:M0=3M-2 X (六)极差 粗略估计一组观察值的变异大小。计算简便,但指标不太稳定。 R=最大值-最小值 (七)四分位数间距 反映观察值中间 1/2 部分的变异,指标较为稳定。 Q=P75-P25=Q3-Q1 11

R 00203 (八)方差反映一组数据中每个变量值与其均数之间的变异,指标稳定而全面,但 其单位为原始数据单位的平方。有时使用不太方便。 1.总体方差σ2=∑(X-μ)2N 2.样本方差S2-Σ(X-X)1(n-1) (九)标准差 1.总体标准差σ=√∑(X-4}/N 2.样本标准差S=∑(X-}/n-1) 3.常用计算公式 ①直接法用于变量值较少时。 S=V∑X2-区]/n1m-1) ②加权法用于变量值较多时 S=∑x2-(∑]1nEf-) ③简捷法用于变量值较多时。 S=V∑X2-∑1川∑f-1)×) (十)变异系数用于①不同度量单位的比较:②两均数相差较大。该指标为无量纲 指标,一般不宜大于15~20%。 公式CV=(S/x)x100%。 三、习题 1.根据下表资料:①编制频数表及绘制频数分布图,简述其分布特征:②计算X、 S、S2、R、CV:③计算x±S,x±1.96S,x±2.58S的范围,估计总体均数 95%和99%的可信区间,并比较各实际分布与理论分布:④现测得二名女学 生血清总蛋白含量,甲生为65.0克/升,乙生为83.0克/升,问二人的血清总 蛋白含量是否正常?解释其临床意义。 12
P1 P25 P50 P75 P100 Q1 Q2 Q3 (八)方差 反映一组数据中每个变量值与其均数之间的变异,指标稳定而全面,但 其单位为原始数据单位的平方。有时使用不太方便。 1. 总体方差 σ2 =∑(X-μ)2 /N 2. 样本方差 S2 =∑(X- X )2 /(n-1) (九)标准差 1. 总体标准差 = ∑(X − ) / N 2 σ µ 2. 样本标准差 = ∑( ) − /( −1) 2 S X x n 3. 常用计算公式 ①直接法 用于变量值较少时。 [ ( ) ] / /( ) 1 2 2 S = ∑ ∑ X − fx n n − ②加权法 用于变量值较多时。 [ ( ) ( ]/ / 1) 2 2 S = ∑ ∑ fX − fx n ∑ f − ③简捷法 用于变量值较多时。 S = [∑ ∑ fX − ( fx) ( / n]/ ∑ f −1)× (i) 2 2 (十)变异系数 用于①不同度量单位的比较;②两均数相差较大。该指标为无量纲 指标,一般不宜大于 15~20%。 公式 CV = (S / x)×100% 。 三、习题 1. 根据下表资料:①编制频数表及绘制频数分布图,简述其分布特征;②计算 X 、 S、S2 、R、CV;③计算 x ±S, x ±1.96S, x ±2.58S的范围,估计总体均数 95%和 99%的可信区间,并比较各实际分布与理论分布;④现测得二名女学 生血清总蛋白含量,甲生为 65.0 克/升,乙生为 83.0 克/升,问二人的血清总 蛋白含量是否正常?解释其临床意义。 12
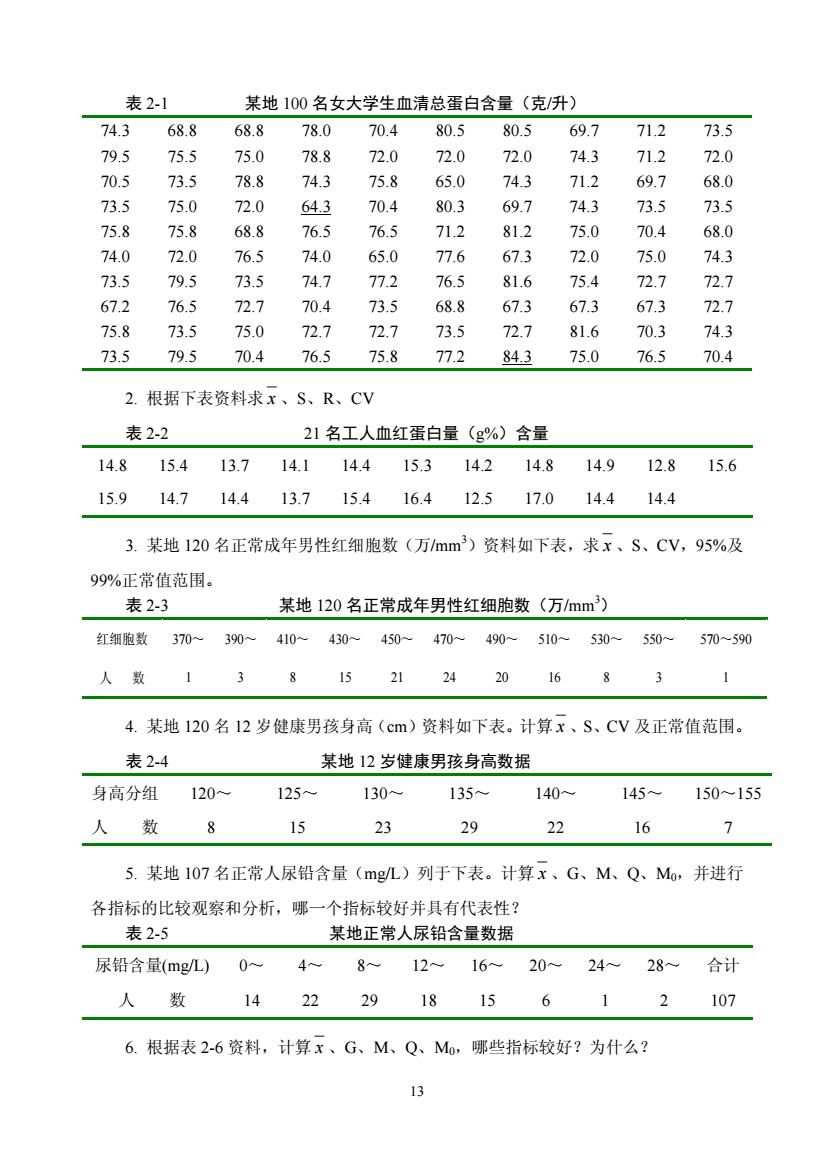
表2-1 某地100名女大学生血清总蛋白含量(克/升) 74.3 68.8 68.8 78.0 70.4 80.5 80.5 697 71.2 73.5 79.5 75.5 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0 70.5 73.5 78.8 74.3 75.8 65.0 74.3 712 69.7 68.0 73.5 75.0 72.0 64.3 70.4 80.3 69.7 74.3 73.5 73.5 75.8 75.8 68.8 76.5 76.5 71.2 81.2 75.0 70.4 68.0 74.0 72.0 76.5 74.0 65.0 77.6 67.3 20 75.0 74.3 735 79.5 735 747 772 76.5 81.6 754 727 72.7 67.2 76.5 72.7 70.4 73.5 68.8 67.3 67.3 67.3 72.7 758 735 75.0 72.7 72.7 73.5 72.7 81.6 70.3 74.3 73.5 79.5 70.4 76.5 75.8 77.2 84.3 75.0 76.5 70.4 2.根据下表资料求x、S、R、CV 表2-2 21名工人血红蛋白量(g%)含量 14.815.413.714.114.415.314.214.814.912.8 15.6 15.914.714.413.715.416.412.517.014.414.4 3.某地120名正常成年男性红细胞数(万mm3)资料如下表,求x、S、CV,95%及 99%正常值范围。 表2-3 某地120名正常成年男性红细胞数(万mm3) 红细胞数370~390~410~430~4350~470~490~510~530~550~570~590 人数 1 3 8 15212420168 1 4.某地120名12岁健康男孩身高(cm)资料如下表。计算x、S、CV及正常值范围。 表2-4 某地12岁健康男孩身高数据 身高分组120~ 125~ 130135~140 145 150~155 人数 8 15 23 29 22 16 7 5.某地107名正常人尿铅含量(mgL)列于下表。计算x、G、M、Q、Mo,并进行 各指标的比较观察和分析,哪一个指标较好并具有代表性? 表2-5 某地正常人尿铅含量数据 尿铅含量(mg/L)0~4~8~12>16>20>24~28~合计 人数 14 22 291815 6 1 2 107 6.根据表2-6资料,计算x、G、M、Q、Mo,哪些指标较好?为什么? 13
表 2-1 某地 100 名女大学生血清总蛋白含量(克/升) 74.3 68.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.5 79.5 75.5 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0 70.5 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.0 73.5 75.0 72.0 64.3 70.4 80.3 69.7 74.3 73.5 73.5 75.8 75.8 68.8 76.5 76.5 71.2 81.2 75.0 70.4 68.0 74.0 72.0 76.5 74.0 65.0 77.6 67.3 72.0 75.0 74.3 73.5 79.5 73.5 74.7 77.2 76.5 81.6 75.4 72.7 72.7 67.2 76.5 72.7 70.4 73.5 68.8 67.3 67.3 67.3 72.7 75.8 73.5 75.0 72.7 72.7 73.5 72.7 81.6 70.3 74.3 73.5 79.5 70.4 76.5 75.8 77.2 84.3 75.0 76.5 70.4 2. 根据下表资料求 x 、S、R、CV 表 2-2 21 名工人血红蛋白量(g%)含量 14.8 15.4 13.7 14.1 14.4 15.3 14.2 14.8 14.9 12.8 15.6 15.9 14.7 14.4 13.7 15.4 16.4 12.5 17.0 14.4 14.4 3. 某地 120 名正常成年男性红细胞数(万/mm 3 )资料如下表,求 x 、S、CV,95%及 99%正常值范围。 表 2-3 某地 120 名正常成年男性红细胞数(万/mm 3 ) 红细胞数 370~ 390~ 410~ 430~ 450~ 470~ 490~ 510~ 530~ 550~ 570~590 人 数 1 3 8 15 21 24 20 16 8 3 1 4. 某地 120 名 12 岁健康男孩身高(cm)资料如下表。计算 x 、S、CV 及正常值范围。 表 2-4 某地 12 岁健康男孩身高数据 身高分组 120~ 125~ 130~ 135~ 140~ 145~ 150~155 人 数 8 15 23 29 22 16 7 5. 某地 107 名正常人尿铅含量(mg/L)列于下表。计算 x 、G、M、Q、M0,并进行 各指标的比较观察和分析,哪一个指标较好并具有代表性? 表 2-5 某地正常人尿铅含量数据 尿铅含量(mg/L) 0~ 4~ 8~ 12~ 16~ 20~ 24~ 28~ 合计 人 数 14 22 29 18 15 6 1 2 107 6. 根据表 2-6 资料,计算 x 、G、M、Q、M0,哪些指标较好?为什么? 13

表2-6 某病50例患者潜伏期数据 潜伏期(小时)12~24~36~48~60~72~84~96~108~合计 人数 7 7 5 4 50 7.根据下表计算x、G、M、M、Q,哪些指标较好,为什么? 表2-7 94名电光性眼炎病人潜伏期资料 潜伏期小时0~24~6~8~10~12~1416>1820~22~24~合计 人数 810 211926401001294 8.据下列资料:求x、G、M、Q,不同人群选择哪些指标较好?为什么? 表2-8 不同人群血清效价资料 不同人群≤1:81:161:321:641:1281:2561:512≥1:1024n 1结核样型 23 10 11 15 1611 8 6 100 瘤型 7 22 394126 32 200 正常人 22 4 5 7 4 0 1 45 9.表2-9 102名健康人的钩端螺旋体血凝抗体滴度分布。求平均滴度。 抗体滴度 1:100 1:200 1:400 1:800 1:1600 合计 人数 7 19 34 29 13 102 10.表2-10 42人接种麻疹疫苗,一月后的血凝抑制抗体滴度分析。求平均抗体滴度。 抗体滴度1:41:81:161:321:641:1281:2561:512合计 人数 1 5 8 2 7 10 4 5 42 四、思考题 1.解释名词:总体样本计量资料计数资料等级资料圆形资料概率 中位数自由度 平均数标准差方差变异系数极差四分位数间距 2.写出频数表的编制方法和步骤,其意义是什么? 3.算术均数、几何均数、中位数的意义、区别及特点是什么? 4.写出平均指标及变异指标的计算公式及应用条件。 5.简述正态分布的特点及意义,哪些医学资料属于正态分布?举出10~20个实例给 以说明。 6.正态分布下的面积分布规律是什么?有哪些公式?举例说明。 7.正常值范围有哪几种,有何意义?举例说明。 14
表 2-6 某病 50 例患者潜伏期数据 潜伏期(小时) 12~ 24~ 36~ 48~ 60~ 72~ 84~ 96~ 108~ 合计 人 数 1 7 11 11 7 5 4 2 2 50 7. 根据下表计算 x 、G、M、M0、Q,哪些指标较好,为什么? 表 2-7 94 名电光性眼炎病人潜伏期资料 潜伏期(小时) 0~ 2~ 4~ 6~ 8~ 10~ 12~ 14~ 16~ 18~ 20~ 22~ 24~ 合计 人 数 8 10 21 19 22 6 4 0 1 0 0 1 2 94 8. 据下列资料:求 x 、G、M、Q,不同人群选择哪些指标较好?为什么? 表 2-8 不同人群血清效价资料 不同人群 ≤1:8 1:16 1:32 1:64 1:128 1:256 1:512 ≥1:1024 n 1 结核样型 23 10 11 15 16 11 8 6 100 瘤 型 25 8 7 22 39 41 26 32 200 正 常 人 22 4 5 5 7 4 0 1 45 9. 表 2-9 102 名健康人的钩端螺旋体血凝抗体滴度分布。求平均滴度。 抗体滴度 1:100 1:200 1:400 1:800 1:1600 合计 人 数 7 19 34 29 13 102 10. 表 2-10 42 人接种麻疹疫苗,一月后的血凝抑制抗体滴度分析。求平均抗体滴度。 抗体滴度 1:4 1:8 1:16 1:32 1:64 1:128 1:256 1:512 合计 人 数 1 5 8 2 7 10 4 5 42 四、思考题 1. 解释名词:总体 样本 计量资料 计数资料 等级资料 圆形资料 概率 中位数 自由度 平均数 标准差 方差 变异系数 极差 四分位数间距 2. 写出频数表的编制方法和步骤,其意义是什么? 3. 算术均数、几何均数、中位数的意义、区别及特点是什么? 4. 写出平均指标及变异指标的计算公式及应用条件。 5. 简述正态分布的特点及意义,哪些医学资料属于正态分布?举出 10~20 个实例给 以说明。 6. 正态分布下的面积分布规律是什么?有哪些公式?举例说明。 7. 正常值范围有哪几种,有何意义?举例说明。 14

8.计算正常值范围(参考值范围)的方法有哪些?各有哪些特点及应用条件? 15
8. 计算正常值范围(参考值范围)的方法有哪些?各有哪些特点及应用条件? 15