
K-means?算法 定义 k-平均算法(英文:k-means clustering)源于信号处理中 的一种向量量化方法,现在则更多地作为一种聚类分析方 法流行于数据挖掘领域。k-平均聚类的目的是:把个点 (可以是样本的一次观察或一个实例)划分到k个聚类中, 使得每个点都属于离他最近的均值(此即聚类中心)对应 的聚类,以之作为聚类的标准
K-means算法 定义 k-平均算法(英文:k-means clustering)源于信号处理中 的一种向量量化方法,现在则更多地作为一种聚类分析方 法流行于数据挖掘领域。k-平均聚类的目的是:把n个点 (可以是样本的一次观察或一个实例)划分到k个聚类中, 使得每个点都属于离他最近的均值(此即聚类中心)对应 的聚类,以之作为聚类的标准

K-means?算法 原理 K-Meas算法的思想很简单,对于给定的样本集,按照样 本之间的距离大小,将样本集划分为K个簇。让簇内的点尽 量紧密的连在一起,而让簇间的距离尽量的大。 如果用数据表达式表示,假设簇划分为(C1,C2,…Cx) 则我们的目标是最小化平方误差E: E=∑1∑rec;lIx-ul3 其中u是簇Ci的均值向量,就是那一簇里所有点的平均! 因为是NP难问题,所以我们不直接求最小值,我们选择了 迭代
K-means算法 原理 K-Means算法的思想很简单,对于给定的样本集,按照样 本之间的距离大小,将样本集划分为K个簇。让簇内的点尽 量紧密的连在一起,而让簇间的距离尽量的大。 如果用数据表达式表示,假设簇划分为 则我们的目标是最小化平方误差E: 其中ui是簇Ci的均值向量,就是那一簇里所有点的平均. 因为是NP难问题,所以我们不直接求最小值,我们选择了 迭代
K-means算法 K-means.算法迭代流程 图a为数据点,图b中,我们随机选择了两 个k类所对应的类别质心,即图中的红色质 心和蓝色质心,然后分别求样本中所有点 到这两个质心的距离,并标记每个样本的 类别为和该样本距离最小的质心的类别, a b c 如图c所示,经过计算样本和红色质心和蓝 色质心的距离,我们得到了所有样本点的 三 第一轮迭代后的类别。此时我们对我们当 前标记为红色和蓝色的点分别求其新的质 心,如图d所示,新的红色质心和蓝色质心 的位置已经发生了变动。图e和图重复了 我们在图c和图d的过程,即将所有点的类 别标记为距离最近的质心的类别并求新的 d 质心。最终我们得到的两个类别如图
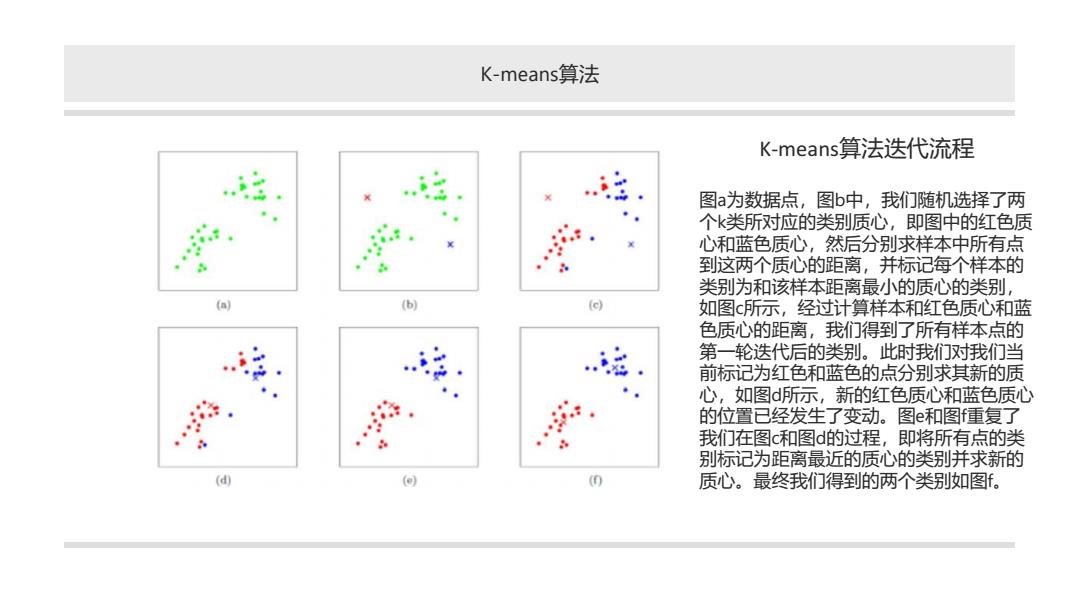
K-means算法 K-means算法迭代流程 图a为数据点,图b中,我们随机选择了两 个k类所对应的类别质心,即图中的红色质 心和蓝色质心,然后分别求样本中所有点 到这两个质心的距离,并标记每个样本的 类别为和该样本距离最小的质心的类别, 如图c所示,经过计算样本和红色质心和蓝 色质心的距离,我们得到了所有样本点的 第一轮迭代后的类别。此时我们对我们当 前标记为红色和蓝色的点分别求其新的质 心,如图d所示,新的红色质心和蓝色质心 的位置已经发生了变动。图e和图f重复了 我们在图c和图d的过程,即将所有点的类 别标记为距离最近的质心的类别并求新的 质心。最终我们得到的两个类别如图f

K-means?算法 算法流程 输入输出 ·输入是样本集D=x1,x2,…cm聚类的簇树k,最大迭代次数N ·输出是簇划分C=C,C2,Ck 流程 ·从数据集D中随机选择k个样本作为初始的k个质心向量:1,2,,k 。对于n=1,2,N 。将簇划分C初始化为空 。对于i=1,2m,计算样本x和各个质心向量uj(0=1,2,k)的距离:d=x:一u,将x标 记最小的为d;所对应的类别入: 。更新C的分类 。对于所有类计算他们新的中心 。重复2-4步,直到质心向量没有发生变化 。输出最后的C
K-means算法 算法流程