
如何根据样本来估计未知参数,这就是参数估计问题.与其他总体相比,正态总体参数的置 信区间是最完善的,应用也最广泛。在构造正态总体参数的置信区间的过程中,【分布、X分 布、F分布以及标准正态分布N(O,)扮演了重要角色.由于正态分布具有对称性,利用双侧 分位数来计算未知参数的置信度为1一α的置信区间,其区间长度在所有这类区间中是最短 的。 第九章假设检验 1.基本内容: 9.1假设检验的基本概念 9.2单个正态总体的假设检验 9.3两个正态总体的假设检验 9.4总体分布X检验法。 2.教学基本要求: (1)理解显著性检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产 生的两类错误。 (2)了解单个及两个正态总体的均值和方差的假设检验。 (3) 了解假设的X己检验法 3.教学重点: 正态总体的假设检验。 4.教学难点: 总体分布的X检验法。 5.教学建议: 我们要根据样本所提供的信总以及运用适当的统计量,对提出的假设作出接受或拒绝 的决策,假设检验是作出这一决策的过程.参数假设检验针对总体分布函数中的未知参数提 出的假设进行检验,非参数假设检验针对总体分布函数形式或类型的假设进行检验。 所有单参数假设检验的内容也适用于多参数与非参数假设检验问题,对多参数假设检 验问题,要寻求一个包含所有待检验参数的检验统计量,使之服从一个已知的确定分布。 四、教学环节与学时分配 序 号 教学内容 总学 其中 时 讲课 习题课其他备注
如何根据样本来估计未知参数,这就是参数估计问题. 与其他总体相比, 正态总体参数的置 信区间是最完善的,应用也最广泛。在构造正态总体参数的置信区间的过程中,t 分布、 2 χ 分 布、F 分布以及标准正态分布 N(0,1) 扮演了重要角色. 由于正态分布具有对称性, 利用双侧 分位数来计算未知参数的置信度为1−α 的置信区间, 其区间长度在所有这类区间中是最短 的。 第九章 假设检验 1.基本内容: 9.1 假设检验的基本概念 9.2 单个正态总体的假设检验 9.3 两个正态总体的假设检验 9.4 总体分布 2 χ 检验法. 2.教学基本要求: (1) 理解显著性检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产 生的两类错误。 (2) 了解单个及两个正态总体的均值和方差的假设检验。 (3) 了解假设的 2 χ 检验法。 3.教学重点: 正态总体的假设检验。 4.教学难点: 总体分布的 2 χ 检验法。 5.教学建议: 我们要根据样本所提供的信息以及运用适当的统计量, 对提出的假设作出接受或拒绝 的决策, 假设检验是作出这一决策的过程. 参数假设检验针对总体分布函数中的未知参数提 出的假设进行检验, 非参数假设检验针对总体分布函数形式或类型的假设进行检验。 所有单参数假设检验的内容也适用于多参数与非参数假设检验问题, 对多参数假设检 验问题, 要寻求一个包含所有待检验参数的检验统计量, 使之服从一个已知的确定分布。 四、教学环节与学时分配 序 号 教学内容 总学 时 其 中 备 注 讲课 习题课 其他 26
1 第一章 6 第二章 3 第三章 4 第四章 第五竞 6 第六章 7 第七章 第八章 第九章 10 总复习 五、教学中应注意的问题:无 六、实验实践内容: 第一章、第二章、第三章配合课堂教学内容,每章安排一次习题课,第四章、第五章安 排一次习题课,第七章、第八章、第九章安排一次习题课。 七、考核方式: 见《概率论与数理统计B》课程考试大纲。 八、教材及主要参考书: 1、选用教材: 《概率论与数理统计》,复旦大学出版社,廖茂新,廖基定主编,201年8月。 2、主要参考书: 《概率论与数理统计》,浙江大学盛骤等编高等教育出版社,1989年8月。 《哈尔滨理工大学数学学习指导·概率论与数理统计》,哈尔滨理工大学数学系编写。 《概率论与数理统计》,由哈尔滨理工大学赵辉副教授主编,东北林业大学出版,2000 年1月。 《概率论与数理统计》,哈尔滨工业大学曹彬等编哈尔滨工业大学出版社。 九、教改说明及其他:无。 执笔人:刘邵容系室审核人:王恒太
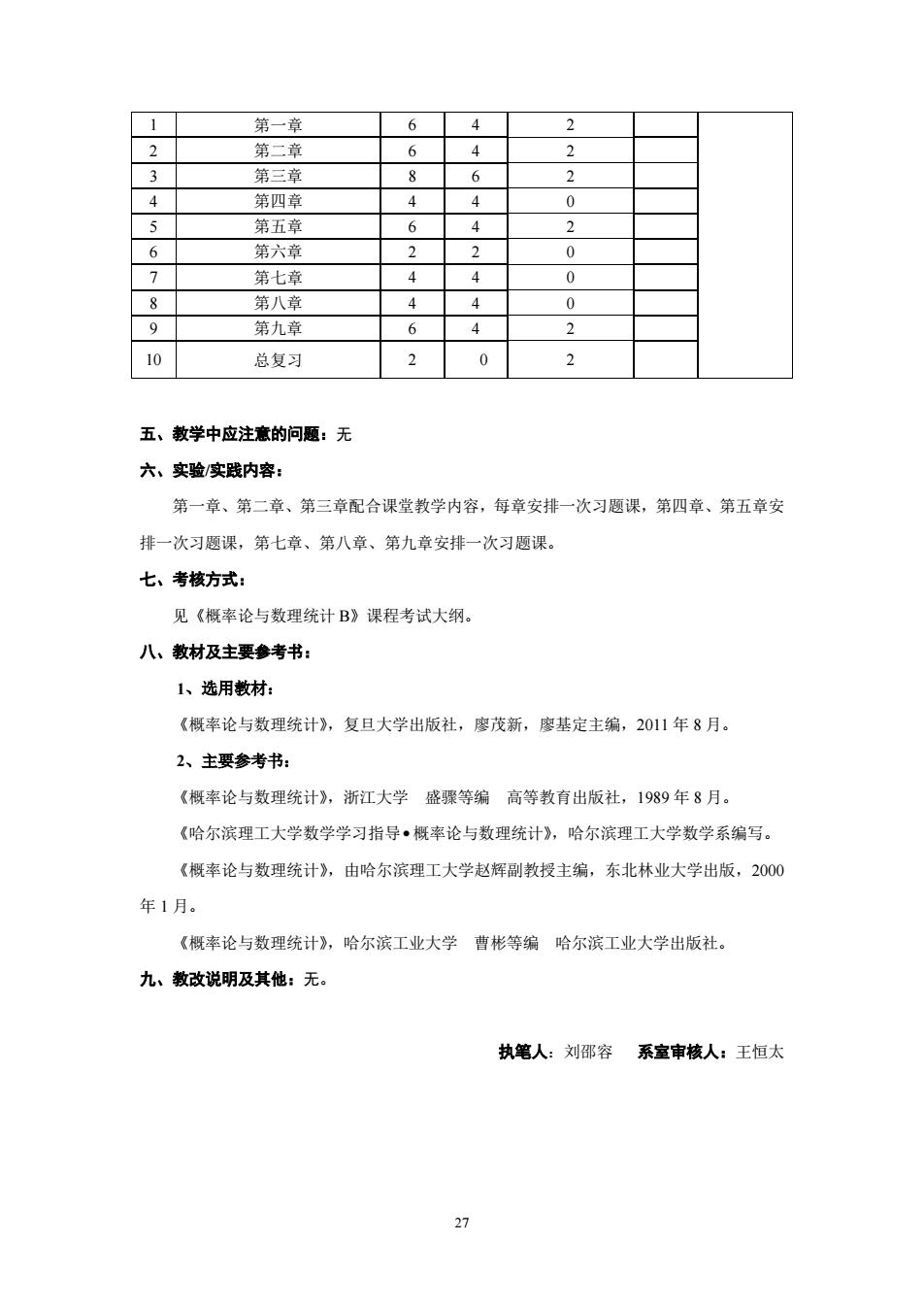
1 第一章 6 4 2 2 第二章 6 4 2 3 第三章 8 6 2 4 第四章 4 4 0 5 第五章 6 4 2 6 第六章 2 2 0 7 第七章 4 4 0 8 第八章 4 4 0 9 第九章 6 4 2 10 总复习 2 0 2 五、教学中应注意的问题:无 六、实验/实践内容: 第一章、第二章、第三章配合课堂教学内容,每章安排一次习题课,第四章、第五章安 排一次习题课,第七章、第八章、第九章安排一次习题课。 七、考核方式: 见《概率论与数理统计 B》课程考试大纲。 八、教材及主要参考书: 1、选用教材: 《概率论与数理统计》,复旦大学出版社,廖茂新,廖基定主编,2011 年 8 月。 2、主要参考书: 《概率论与数理统计》,浙江大学 盛骤等编 高等教育出版社,1989 年 8 月。 《哈尔滨理工大学数学学习指导• 概率论与数理统计》,哈尔滨理工大学数学系编写。 《概率论与数理统计》,由哈尔滨理工大学赵辉副教授主编,东北林业大学出版,2000 年 1 月。 《概率论与数理统计》,哈尔滨工业大学 曹彬等编 哈尔滨工业大学出版社。 九、教改说明及其他:无。 执笔人:刘邵容 系室审核人:王恒太 27

《概率论与数理统计B》课程考试大纲 课程编号:130704002 总学时数:48学时学分:3学分 一、考试对象:修完木课程所规定的各专业学生, 二、考试目的 本课程考试目的是熟练掌握概率论与数理统计中的基本理论和分析方法,能熟练运用 基本原理解决某些实际问题。 三、考试要求 本课程是一门理论性很强的基础性学科,要求学生对基本理论的了解和掌握,同时具备 较强的解决实际问题的能力。 四、考试内容与要求 第一章随机事件及概率15-20分值 1、考试内容:①随机事件的关系及其运算:②古典概型、几何概型:③条件概率、 全概率公式与贝叶斯公式:④事件的独立性。 2、考试要求:全面了解随机事件的概念、关系、运算等基本问题,掌握概率的性质与 运用,会计算古典概型、几何概型以及条件概率,掌握全概率公式与贝叶斯公式的运用,了 解随机事件独立性的概念以及伯努利概型,掌握事件独立性与概率的运算。 第二章随机变量及其分布1215分值 1、考试内容:①随机变量的概率密度与分布函数:②离散型随机变量及其分布:③连 续型随机变量及其分布。 2、考试要求:了解随机变量的定义,掌握分布函数与概率密度函数的性质与关系,掌 握01分布,二项分布与泊松分布的分布律和分布函数,掌握均匀分布,指数分布与正态分 布的概率密度和分布函数,会求离散型随机变量的分布率与分布函数,求连续型随机变量的 概率密度函数与分布函数。 第三章多维随机变量及其分布12-15分值 1、考试内容:①二维随机变量的联合分布函数、边缘分布函数:②二维离散型随机 变量的条件分布律、边缘分布律:③二维连续型随机变量的边缘概率密度、条件概率密度: ④二维均匀分布、二维正态分布的概率密度与相关概率计算:⑤多维随机变量的独立性。 2、考试要求:全面了解并掌握二维随机变量联合分布、条件分布、边缘分布等基本概
《概率论与数理统计 B》课程考试大纲 课程编号:130704002 总学时数:48 学时 学分:3 学分 一、考试对象:修完本课程所规定的各专业学生。 二、考试目的 本课程考试目的是熟练掌握概率论与数理统计中的基本理论和分析方法,能熟练运用 基本原理解决某些实际问题。 三、考试要求 本课程是一门理论性很强的基础性学科,要求学生对基本理论的了解和掌握,同时具备 较强的解决实际问题的能力。 四、考试内容与要求 第一章 随机事件及概率 15-20 分值 1、考试内容: ① 随机事件的关系及其运算;② 古典概型、几何概型;③ 条件概率、 全概率公式与贝叶斯公式;④事件的独立性。 2、考试要求:全面了解随机事件的概念、关系、运算等基本问题,掌握概率的性质与 运用,会计算古典概型、几何概型以及条件概率,掌握全概率公式与贝叶斯公式的运用,了 解随机事件独立性的概念以及伯努利概型,掌握事件独立性与概率的运算。 第二章 随机变量及其分布 12-15 分值 1、考试内容:①随机变量的概率密度与分布函数;②离散型随机变量及其分布;③ 连 续型随机变量及其分布。 2、考试要求:了解随机变量的定义,掌握分布函数与概率密度函数的性质与关系,掌 握 0-1 分布,二项分布与泊松分布的分布律和分布函数,掌握均匀分布,指数分布与正态分 布的概率密度和分布函数,会求离散型随机变量的分布率与分布函数,求连续型随机变量的 概率密度函数与分布函数。 第三章 多维随机变量及其分布 12-15 分值 1、考试内容: ① 二维随机变量的联合分布函数、边缘分布函数;②二维离散型随机 变量的条件分布律、边缘分布律;③二维连续型随机变量的边缘概率密度、条件概率密度; ④二维均匀分布、二维正态分布的概率密度与相关概率计算;⑤多维随机变量的独立性。 2、考试要求:全面了解并掌握二维随机变量联合分布、条件分布、边缘分布等基本概 28

念以及相关运算问题,掌握二维均匀分布、二维正态分布的概率密度与相关概率计算:把握 随机变量的独立性,并能运用独立性解决实际问题。 第四章随机变量函数的分布812分值 1、考试内容:①离散型随机变量函数的分布:②连续型随机变量函数的分布 2、考试要求:会求离散型随机变量函数的分布律,掌握常见连续型随机变量函数的分 布。 第五章随机变量的数字特征1215分值 1、考试内容:①随机变量的数学期望:②随机变量的方差:③随机变量函数的数学 期望与方差:④随机变量的数学期望与方差的性质:⑤随机变量的独立性与相关性。 2、考试要求:掌握0-1分布,二项分布、泊松分布、均匀分布,指数分布、正态分布 的数学期望及方差,掌握随机变量的数学期望与方差的性质及其运用:会求随机变量的函数 的数字特征,判断随机变量的独立性与相关性。 第六章大数定理及其中心极限定理410分值 1、考试内容:①大数定理:②中心极限定理 2、考试要求:掌握大数定理以及中心极限定理的运用。 第七章数理统计的基本概念812分值 1、考试内容:①统计量的定义:②X分布:③1分布:④F分布:⑤正态总体的某 些常用统计量分布。 2、考试要求:了解统计量的定义,掌握X分布、1分布和F分布的定义及性质,了 解分布分位数的概念并会查表计算,尤其是正态总体的某些常用统计量分布情况。 第八章参数估计815分值 1、考试内容:①矩估计:②极大似然估计:③估计量的评判标准④区间估计 2、考试要求:掌握随机变量参数的矩估计与极大似然估计,会用估计量的评判标准判 断估计量,掌握正态总体的区间估计。 第九章假设检验8分值 1、考试内容:①单正态总体的假设检验:②双正态总体的假设检验 2、考试要求:了解假设检验的基本原理:掌握单正态总计的假设检验与双正态总体的 假设检验:了解总体分布的X检验法。 五、考试方式及时间
念以及相关运算问题,掌握二维均匀分布、二维正态分布的概率密度与相关概率计算;把握 随机变量的独立性,并能运用独立性解决实际问题。 第四章 随机变量函数的分布 8-12 分值 1、考试内容:① 离散型随机变量函数的分布;②连续型随机变量函数的分布。 2、考试要求:会求离散型随机变量函数的分布律,掌握常见连续型随机变量函数的分 布。 第五章 随机变量的数字特征 12-15 分值 1、考试内容: ① 随机变量的数学期望;② 随机变量的方差;③随机变量函数的数学 期望与方差;④随机变量的数学期望与方差的性质;⑤随机变量的独立性与相关性。 2、考试要求:掌握 0-1 分布,二项分布、泊松分布、均匀分布,指数分布、正态分布 的数学期望及方差,掌握随机变量的数学期望与方差的性质及其运用;会求随机变量的函数 的数字特征,判断随机变量的独立性与相关性。 第六章 大数定理及其中心极限定理 4-10 分值 1、考试内容:①大数定理;② 中心极限定理 2、考试要求:掌握大数定理以及中心极限定理的运用。 第七章 数理统计的基本概念 8-12 分值 1、考试内容:① 统计量的定义;② 2 χ 分布;③t 分布;④ F 分布;⑤正态总体的某 些常用统计量分布。 2、考试要求:了解统计量的定义,掌握 2 χ 分布、t 分布和 F 分布的定义及性质,了 解分布分位数的概念并会查表计算,尤其是正态总体的某些常用统计量分布情况。 第八章 参数估计 8-15 分值 1、考试内容:① 矩估计; ②极大似然估计;③估计量的评判标准④区间估计 2、考试要求:掌握随机变量参数的矩估计与极大似然估计,会用估计量的评判标准判 断估计量,掌握正态总体的区间估计。 第九章 假设检验 8 分值 1、考试内容:①单正态总体的假设检验;②双正态总体的假设检验 2、考试要求:了解假设检验的基本原理;掌握单正态总计的假设检验与双正态总体的 假设检验;了解总体分布的 2 χ 检验法。 五、考试方式及时间 29

考试方式:闭卷理论考 考试时间:100分钟。 六、考试题型结构及分值分布 选择题:约20% 填空题:约20% 计算题:约50% 证明题:约10% 七、成绩综合评定办法 学生最后总成绩由平时学习过程的考核占*30%,理论闭卷考试成绩占70%,其中平时 学习过程包括平时作业(占总成绩的20%),考勤(占总成绩的5%),课堂表现及课后互动 (占总成绩的5%)。 八、教材及主要参考书:见《概率论与数理统计B》课程教学大纲。 执笔人:刘邵容系室审核人:王恒太
考试方式:闭卷理论考 考试时间:100 分钟。 六、考试题型结构及分值分布 选择题:约 20% 填空题:约 20% 计算题:约 50% 证明题:约 10% 七、成绩综合评定办法 学生最后总成绩由平时学习过程的考核占*30%,理论闭卷考试成绩占 70%,其中平时 学习过程包括平时作业(占总成绩的 20%),考勤(占总成绩的 5%),课堂表现及课后互动 (占总成绩的 5%)。 八、教材及主要参考书:见《概率论与数理统计 B》课程教学大纲。 执笔人:刘邵容 系室审核人:王恒太 30