
MIDAS 一、组合结构计算原理 2.组合截面应力计算一 换算截面特性计算 输入截面及材料特性 项目 数值 备注 混凝士有效弹性模量修订系数 1.000000静力时为1,收缩、徐变根据右侧表格计算 混凝土弹性模量E© 34500.000000 《钢-混凝士组合梁》表3.1.5 钢材弹性模量s 206000.000000 《钢-混凝土组合梁》表3.2.7 工字钢As 341960.000000 钢材自身惯性柜Is 129364655770.800000 钢重心到自身顶距离 1228.820600 钢重心到自身底距离 421.181400AUT0CAD可得,惯性矩及重心均为至自身顶底距离 混凝土截AG 3016496.000000 截面特性中可查程序对应值:A Iyy Czp Czm 混凝土自身惯性矩Ic 24221374366.811800 混凝土重心到自身顶 150.243700 混凝土重心到自身底 199.756300 混凝士桥面板形心 213151 28RR7 组合截面形心 钢梁形机
一、组合结构计算原理 2. 组合截面应力计算——换算截面特性计算
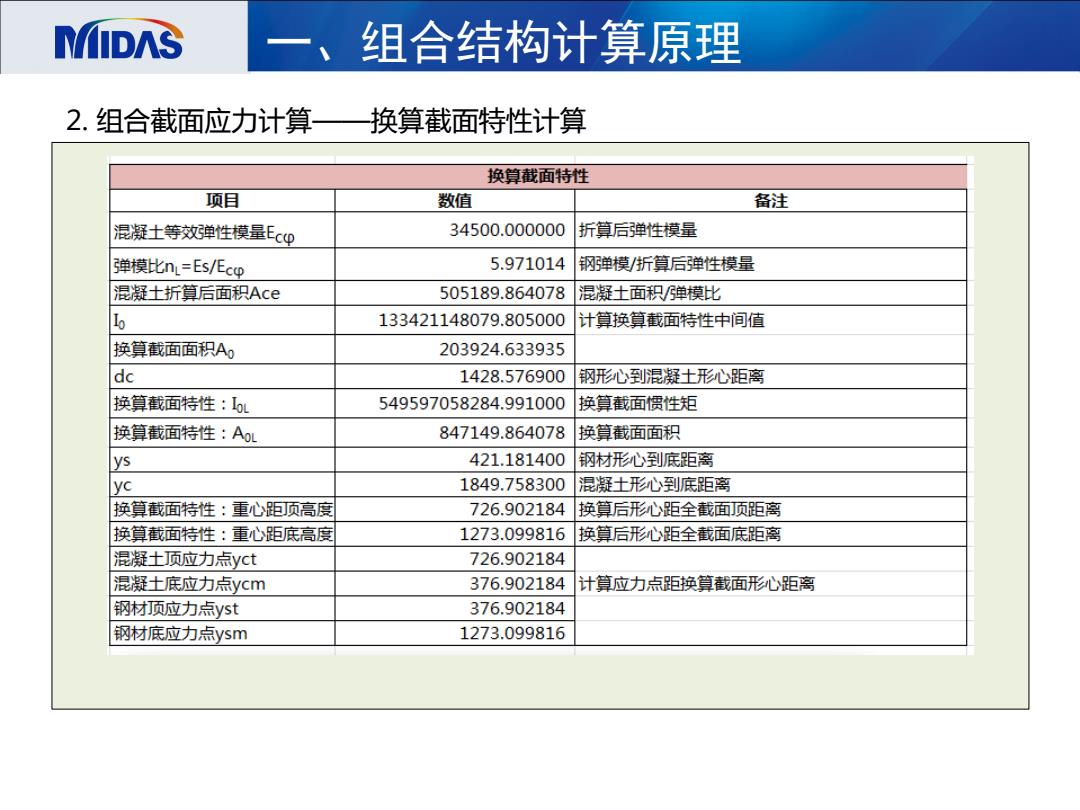
MIDAS 一、组合结构计算原理 2.组合截面应力计算—换算截面特性计算 换算截面特性 项目 数值 备注 混凝士等效弹性模量Ecp 34500.000000 折算后弹性模量 弹模比nL=Es/Ecp 5.971014 钢弹模/折算后弹性模量 混凝土折算后面积Ace 505189.864078 混凝土面积/弹模比 Io 133421148079.805000 计算换算截面特性中间值 换算截面面积A, 203924.633935 dc 1428.576900 钢形心到混凝土形心距离 换算截面特性:lbL 549597058284.991000 换算截面惯性矩 换算截面特性:AoL 847149.864078 换算截面面积 ys 421.181400 钢材形心到底距离 yc 1849.758300 混凝土形心到底距离 换算截面特性:重心距顶高度 726.902184 换算后形心距全截面顶距离 换算截面特性:重心距底高度 1273.099816 换算后形心距全截面底距离 混凝土顶应力点yct 726.902184 混凝土底应力点ycm 376.902184 计算应力点距换算截面形心距离 钢材顶应力点yst 376.902184 钢材底应力点ysm 1273.099816
一、组合结构计算原理 2. 组合截面应力计算——换算截面特性计算
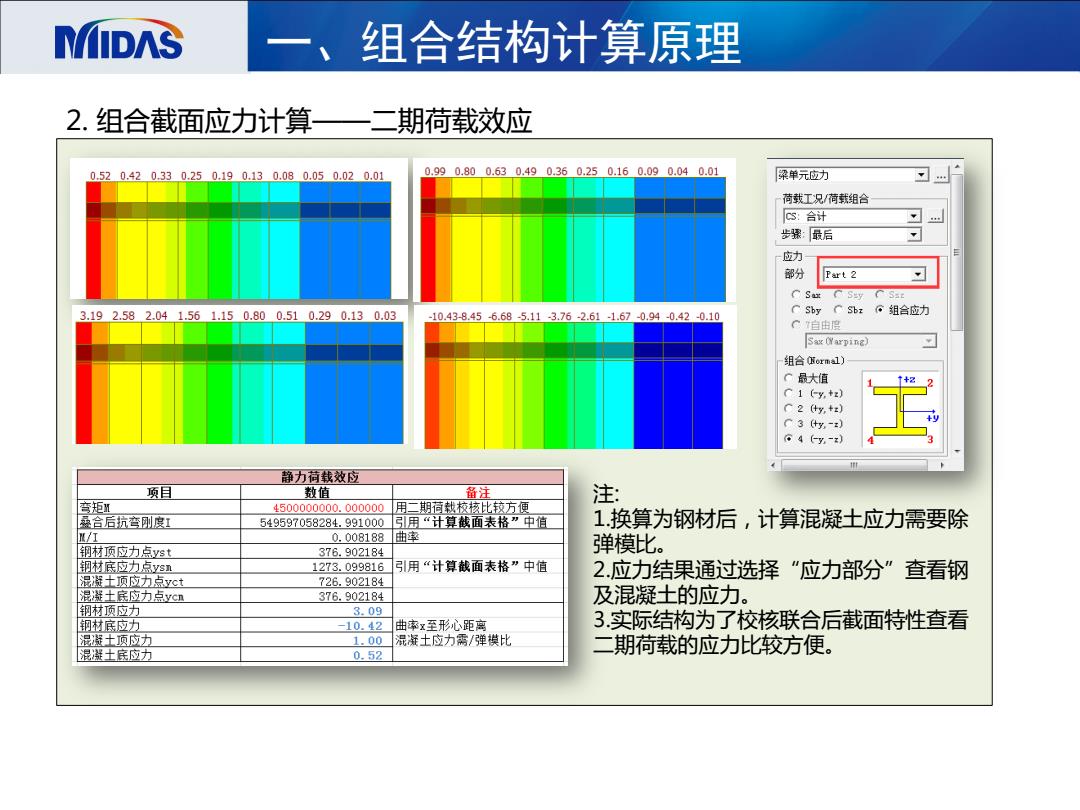
MIDAS 一、组合结构计算原理 2.组合截面应力计算一二 期荷载效应 0.520.420.330.250.190.130.080.050.020.01 0.990.800.630.490.360.250.160.090.040.01 深单元应力 荷载工况/荷载组合 C3:合计 步骤:最后 应力 部分 Part 2 3.192.582.041.561.150.800.510.290.130.03 -10.43-8.45-6.68-5.11-3.76-2.61-1.67-0.94-0.42-0.10 CSby C Sbz组合应力 C自由度 Sax (Yarping) 组合依orm1) C最大值 T+2 C1〔y,r C 2 (y,+:) C3ty-z】 G4 6-y.-2) 静力荷载效应 项目 数值 备注 注: 弯矩1 4500000000.000000用二期荷载校核比较方便 经合后抗弯刚度虹 549597058284.991000写引用“计算截面表格”中值 1换算为钢材后,计算混凝土应力需要除 N/I 0.008188曲率 钢材顶应力点yst 376.902184 弹模比。 钢材底应力点ysn 1273.099816 引用“计算截面表格”中值 混凝士顶应力点yct 2.应力结果通过选择“应力部分”查看钢 726.902184 混凝土底应力点ycn 376.902184 及混凝土的应力。 钢材顶应力 3.09 钢材底应力 -10.42 曲率x至形心距离 3.实际结构为了校核联合后截面特性查看 混凝土顶应力 1.00 混凝土应力需/弹模比 混凝土底应力 二期荷载的应力比较方便。 0.52
一、组合结构计算原理 2. 组合截面应力计算——二期荷载效应 注: 1.换算为钢材后,计算混凝土应力需要除 弹模比。 2.应力结果通过选择“应力部分”查看钢 及混凝土的应力。 3.实际结构为了校核联合后截面特性查看 二期荷载的应力比较方便
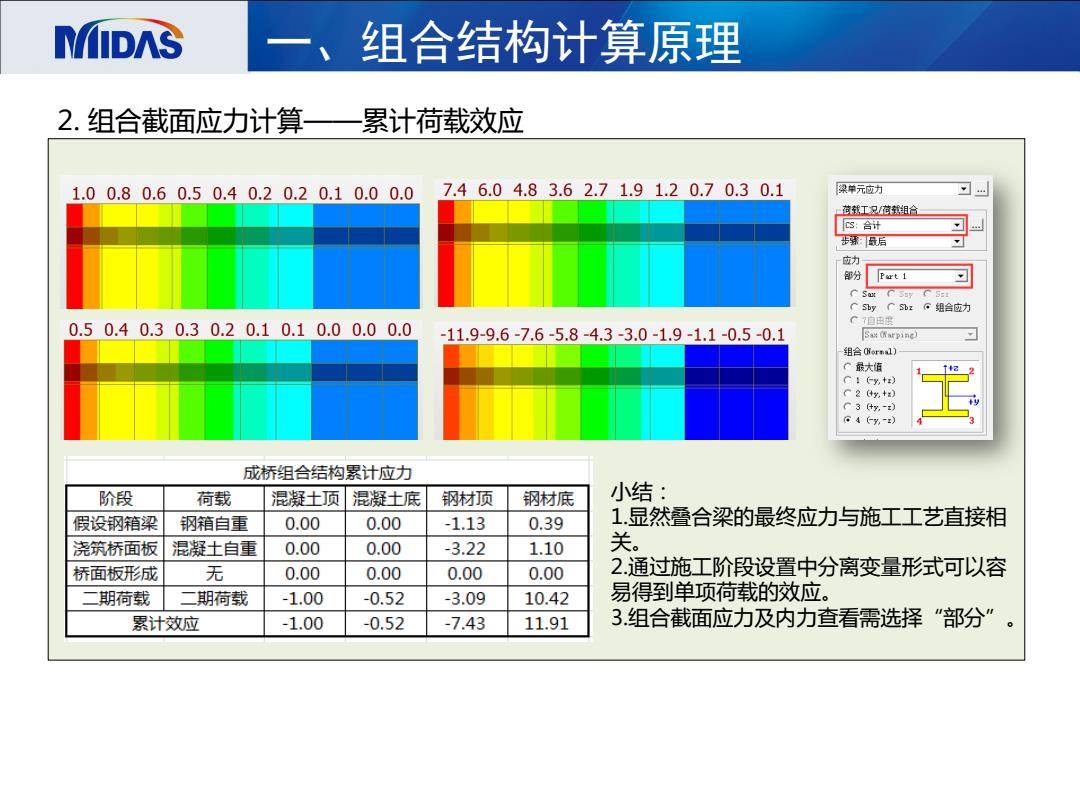
MIDAS 一 组合结构计算原理 2.组合截面应力计算—一 累计荷载效应 1.00.80.60.50.40.20.20.10.00.0 7.46.04.83.62.71.91.20.70.30.1 绿单元应力 芭就工双信载组合 C3:合计 步球低后 应力 部分 C C Ssy C S: Sby C Sbz组合应力 自由 0.50.40.30.30.20.10.10.00.00.0 -11.9-9.6-7.6-5.8-4.3-3.0-1.9-1.1-0.5-0.1 Sax (Warpine) 组合0Nrml】 个最大值 C1 (y,+t) C2y,+0 C34y,-) 4(y,-z) 成桥组合结构累计应力 阶段 荷载 混凝土顶混凝土底 钢材顶 钢材底 小结: 假设钢箱梁 钢箱自重 0.00 0.00 -1.13 0.39 1显然叠合梁的最终应力与施工工艺直接相 浇筑桥面板 混凝土自重 0.00 0.00 -3.22 1.10 关。 桥面板形成 无 0.00 0.00 0.00 0.00 2通过施工阶段设置中分离变量形式可以容 期荷载 期荷载 -1.00 -0.52 -3.09 10.42 易得到单项荷载的效应。 累计效应 -1.00 -0.52 -7.43 11.91 3组合截面应力及内力查看需选择“部分
一、组合结构计算原理 2. 组合截面应力计算——累计荷载效应 小结: 1.显然叠合梁的最终应力与施工工艺直接相 关。 2.通过施工阶段设置中分离变量形式可以容 易得到单项荷载的效应。 3.组合截面应力及内力查看需选择“部分

MIDAS 一、 组合结构计算原理 3.虚拟荷载法计算混凝土板升降温后应力 混凝士柜板形心 混凝士桥面板死形心 Po 湿士桥面板形心 凝士桥面板形○ 年手年手 yoc 组合截面心 组合截形○ + 组合截面形心 组合哉面形心 钢柔形恥 钢梁恥 钢梁形恥 钢深心 B.0.2虚拟荷载法可按下列步骤计算: B.0.3 组合截面各位置处的应力增量可按下列公式计算: 1 假定钢梁与混凝土之间无连接,混凝土桥面板在温度、收 混凝土桥面板截面: 缩等作用下产生自由形变ee, 2根据混凝土桥面板的应变及有效弹性模量求解虚拟荷载 -[+0]-是 (B.0.3-1) P:将该虚拟荷载P。反向施加于混凝土桥面板形心上,使混凝土 钢梁截面: 桥面恢复形变ee。 是+尝 (B.0.3-2) 3 恢复钢梁与混凝土桥面板之间的连接,释放P。,求解截面 应力。 4将以上3个步骤的应力进行叠加。 Po=EAe (ta,-tcae),Mo=Poyoe (B.0.4-7) 注: 1.仅混凝土板升降温,应力计算相对简单,可以通过上述过程非常容易得到其效应。 2收缩徐变与混凝土板降温效应相当,可通过同样方法得到,仅计算集中力P0方法不同
一、组合结构计算原理 3.虚拟荷载法计算混凝土板升降温后应力 𝜀𝑐 𝑃0 𝑃0 𝑦0𝑐 = + + 注: 1.仅混凝土板升降温,应力计算相对简单,可以通过上述过程非常容易得到其效应。 2.收缩徐变与混凝土板降温效应相当,可通过同样方法得到,仅计算集中力P0方法不同