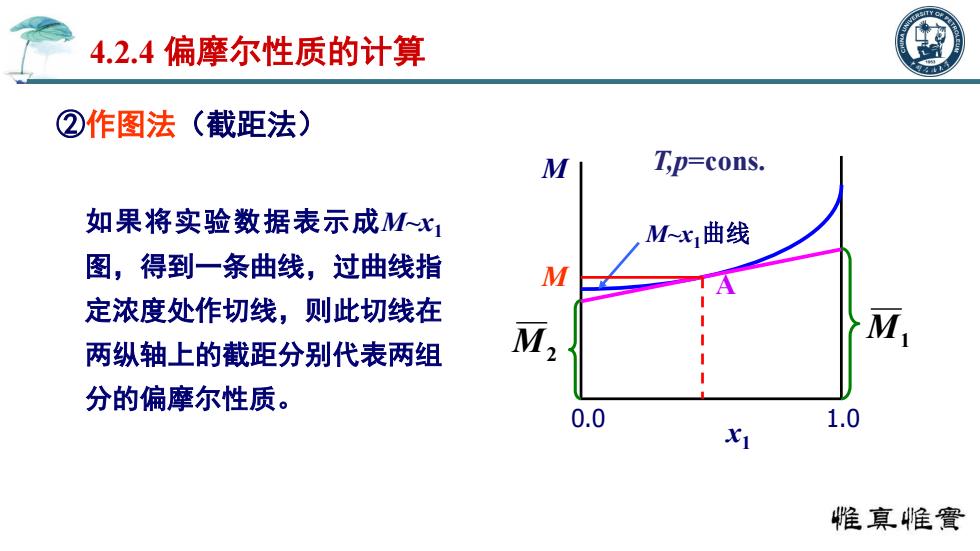
4.2.4偏摩尔性质的计算 ②作图法(截距法) M T,p=cons. 如果将实验数据表示成Mx1 M,曲线 图,得到一条曲线,过曲线指 M 定浓度处作切线,则此切线在 M 两纵轴上的截距分别代表两组 分的偏摩尔性质。 0.0 1.0 x1 惟真帷竇
②作图法(截距法) 如果将实验数据表示成M~x1 图,得到一条曲线,过曲线指 定浓度处作切线,则此切线在 两纵轴上的截距分别代表两组 分的偏摩尔性质。 4.2.4 偏摩尔性质的计算 M2 T,p=cons. M~x1曲线 M x1 0.0 1.0 A M1 M
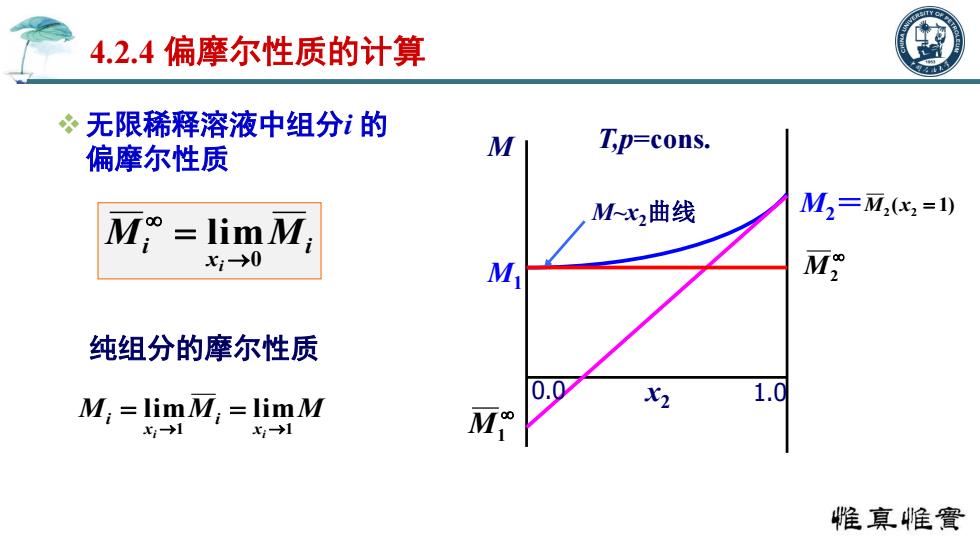
4.2.4偏摩尔性质的计算 无限稀释溶液中组分i的 偏摩尔性质 M Tp=cons. M=lim M; M~x,曲线 M2=M2x2=1) x;→0 M M 纯组分的摩尔性质 M;=limM,limM X2 xi1 x→1 M 惟真帷竇
无限稀释溶液中组分i 的 偏摩尔性质 i x Mi M i 0 lim 4.2.4 偏摩尔性质的计算 M1 M2 T,p=cons. M~x2曲线 M x2 0.0 1.0 M2 = M1 ( 1) M2 x2 M M M i xi i x i 1 1 lim lim 纯组分的摩尔性质

4.2.4偏摩尔性质的计算 P97-100例4-2例4-3(自学) P98例4-4某二元液体混合物在293K、0.10133MPa下的焓可用下式 表示: H=100x1+150x2+x2(10x1+5x2) (A) 式中H单位为JmoH。试确定在该温度、压力下 (1)用x表示的偏摩尔焓五,和H2; (2)纯组分的焓H1和H2的数值; (3)无限稀释溶液的偏摩尔焓五”和五”的数值。 惟真帷竇
P97-100 例4-2 例4-3 (自学) P98例4-4 某二元液体混合物在293K、0.10133MPa下的焓可用下式 表示: H=100x1+150x2+x1x2 (10x1+ 5x2 ) (A) 式中 H单位为J.mol-1。试确定在该温度、压力下 (1)用x1表示的偏摩尔焓 和 ; (2)纯组分的焓H1和H2的数值; (3)无限稀释溶液的偏摩尔焓 和 的数值。 4.2.4 偏摩尔性质的计算 H1 H2 H1 H2

4.2.4偏摩尔性质的计算 解:()根据解析法进行计算 dH H1=H+(1-x dH dx H,=H-X1 x1 将x2=1-x1代入H表达式,并化简得 H=100x1+150(1-x)+x1(1-x)[10x1+5(1-x)】 =150-45x1-5x3 求导: =-45-15x号 dH dx, 惟真帷竇
解:(1) 根据解析法进行计算 将 x2=1-x1 代入H 表达式,并化简得 H=100x1+150(1-x1 )+x1 (1-x1 ) [10x1+5(1-x1 )] =150-45x1-5x1 3 4.2.4 偏摩尔性质的计算 1 1 1 d d (1 ) x H H H x 1 2 1 d d x H H H x 求导: 2 1 1 45 15 d d x x H
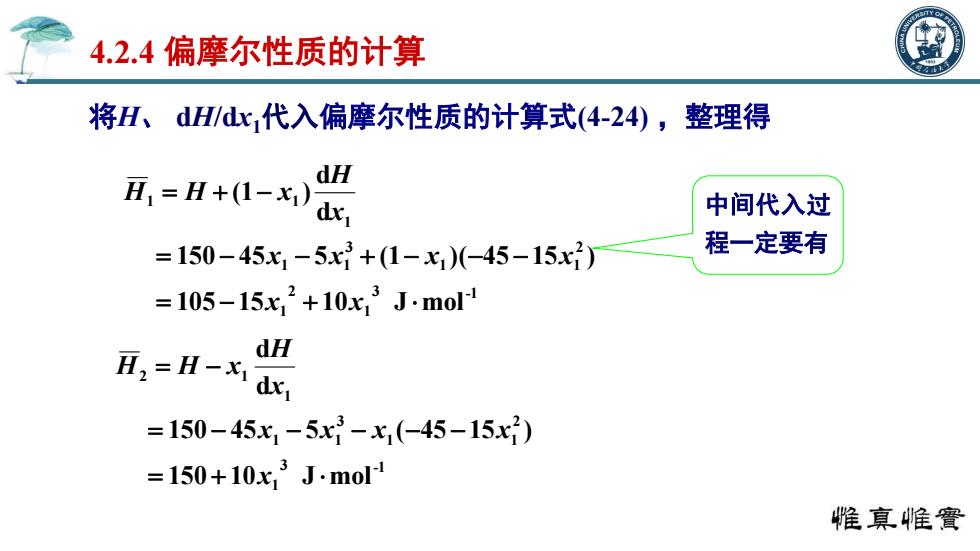
4.2.4偏摩尔性质的计算 将H、dH/x,代入偏摩尔性质的计算式(4-24),整理得 耳,=H+1- dH 中间代入过 =150-45.x1-5x+(1-x1)(-45-15x) 程一定要有 =105-15x2+10x,3Jmol dH 五2=H-dc =150-45x,-5x3-x,(-45-15x) =150+10x13Jmol 惟真帷竇
将H、 dH/dx1代入偏摩尔性质的计算式(4-24) ,整理得 4.2.4 偏摩尔性质的计算 3 -1 1 2 1 2 1 1 3 1 1 1 1 1 105 15 10 J mol 150 45 5 (1 )( 45 15 ) d d (1 ) x x x x x x x H H H x 3 -1 1 2 1 1 3 1 1 1 2 1 150 10 J mol 150 45 5 ( 45 15 ) d d x x x x x x H H H x 中间代入过 程一定要有