中国石油大学（华东）：《化工热力学》课程教学资源（课件讲义）第4章 溶液热力学性质计算

4.2.3偏摩尔性质之间的关系 Maxwell关系式同样也适用于偏摩尔性质。 av, as, D.n T.n D. OG; p =可 a(G;IT) ot T2 T.n D, 惟真帷竇

Maxwell关系式同样也适用于偏摩尔性质。 T n i p n i p S T V , ,                       4.2.3 偏摩尔性质之间的关系 i p n i S T G             , i T n i V p G            , 2 , ( / ) T H T G T i p n i            

4.2.4偏摩尔性质的计算 偏摩尔性质的计算有两种方法： ①解析法 由定义式 -[a9 T,P,ni 可推导出用摩尔性质表达偏摩尔性质的公式 推导过程见教材P95-96 惟真帷竇

偏摩尔性质的计算有两种方法： ① 解析法 由定义式 可推导出用摩尔性质表达偏摩尔性质的公式 推导过程见教材P95-96 4.2.4 偏摩尔性质的计算 T p nj i i i n nM M           , , ( )

4.2.4偏摩尔性质的计算 M=M->x OM (4-23) k≠i )T.p 式中：i代表所讨论的组元； k为不包括i在内的其他组元； j表示不包括i及k的组元 如果已知溶液性质M时，可用上式求算多元系的偏摩尔性质。 惟真帷竇

式中： i 代表所讨论的组元； k 为不包括i 在内的其他组元； j 表示不包括i 及 k 的组元 如果已知溶液性质M 时，可用上式求算多元系的偏摩尔性质。 4.2.4 偏摩尔性质的计算                k i k T p x i k j i k x M M M x , , , (4-23)

4.2.4偏摩尔性质的计算 在T,p恒定的条件下，对二元系，x+x21,则 OM -dM-_dM OM dM dx,dx ax1 T.p.xj.2 dx, TP.xj.2 所以，对二元系偏摩尔性质可写成 dM M1=M+(1-x) d M,=M-x1 dxi (4-24a (4-24b) dM dM (注意dx=一dx2) M=M-x2 dx2 M2=M+(1-x2) dx; 惟真帷竇

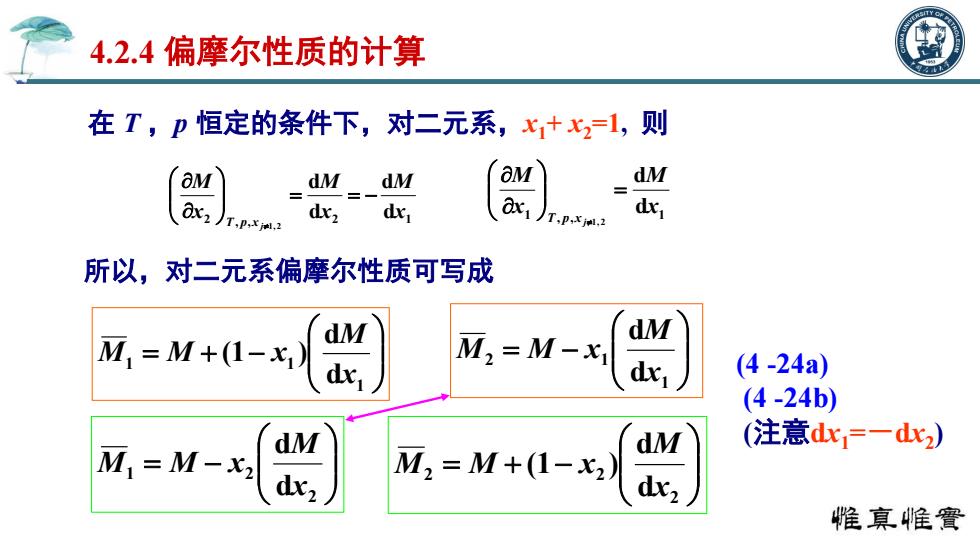
在 T ，p 恒定的条件下，对二元系，x1+ x2=1, 则 2 , , 2 d 1 d d d 1,2 x M x M x M T p x j               4.2.4 偏摩尔性质的计算 1 , , d 1 d 1,2 x M x M T p x j                        1 1 1 d d (1 ) x M M M x d d 1 2 1           x M M M x 所以，对二元系偏摩尔性质可写成           2 1 2 d d x M M M x            2 2 2 d d (1 ) x M M M x (4 -24a) (4 -24b) (注意dx1 =－dx2 )

4.2.4偏摩尔性质的计算 ~通过实验测定在指定T,p下不同组成时的M值，并将实验数 据关联成M-x,的解析式，就可以用解析法求出导数值来计算 偏摩尔性质。 ,也可以用定义式来计算偏摩尔性质。 M: a(nM) T,p,jt 、阿 T,p,njti 惟真帷竇

 通过实验测定在指定T，p下不同组成时的M值，并将实验数 据关联成M-x1的解析式，就可以用解析法求出导数值来计算 偏摩尔性质。  也可以用定义式来计算偏摩尔性质。 4.2.4 偏摩尔性质的计算 j i T p nj i i T p n i i n nM n M M                         , , , , t ( )