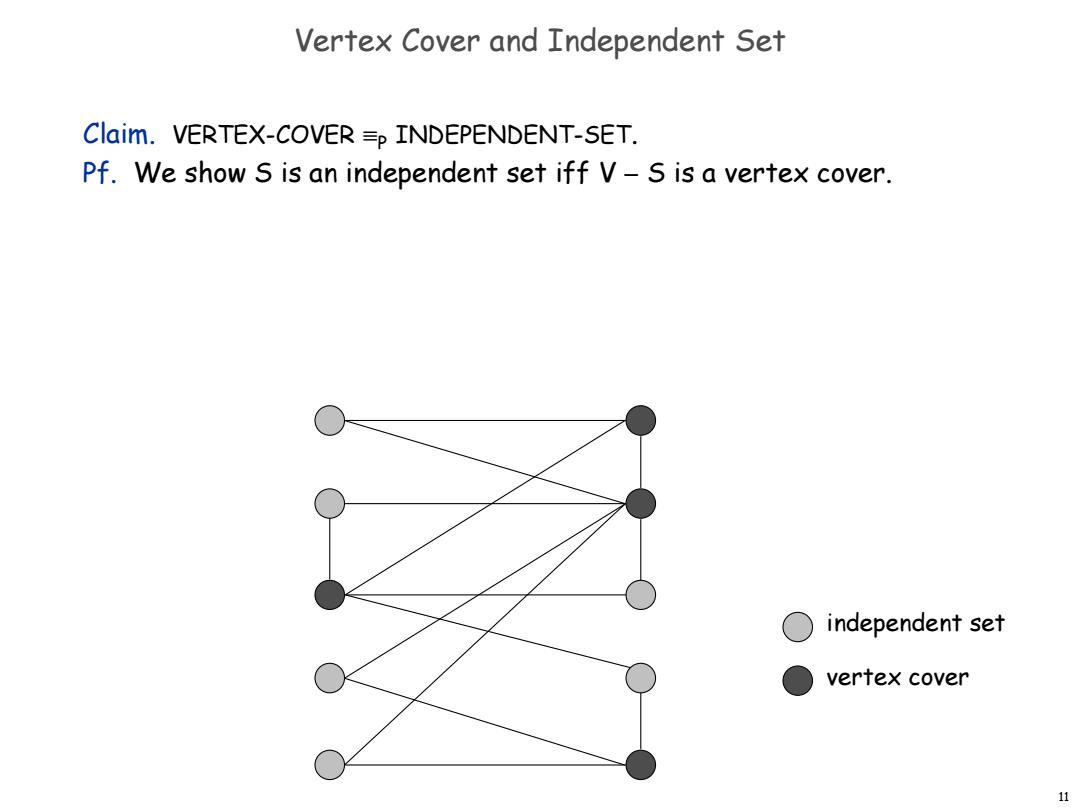
Vertex Cover and Independent Set Claim.VERTEX-COVER =p INDEPENDENT-SET. Pf.We show S is an independent set iff V-S is a vertex cover. independent set vertex cover 11
11 Vertex Cover and Independent Set Claim. VERTEX-COVER P INDEPENDENT-SET. Pf. We show S is an independent set iff V S is a vertex cover. vertex cover independent set

Vertex Cover and Independent Set Claim.VERTEX-COVER =p INDEPENDENT-SET. Pf.We show S is an independent set iff V-S is a vertex cover. → Let S be any independent set. Consider an arbitrary edge (u,v). ,S independent→ug SorveS→u∈V-Sorv∈V-S. Thus,V-S covers (u,v). 仁 Let V-S be any vertex cover. .Consider two nodes u∈S and v∈S. Observe that (u,v)gE since V-S is a vertex cover. Thus,no two nodes in S are joined by an edgeS independent set. 12
12 Vertex Cover and Independent Set Claim. VERTEX-COVER P INDEPENDENT-SET. Pf. We show S is an independent set iff V S is a vertex cover. Let S be any independent set. Consider an arbitrary edge (u, v). S independent u S or v S u V S or v V S. Thus, V S covers (u, v). Let V S be any vertex cover. Consider two nodes u S and v S. Observe that (u, v) E since V S is a vertex cover. Thus, no two nodes in S are joined by an edge S independent set. ▪

Reduction from Special Case to General Case Basic reduction strategies. Reduction by simple equivalence. Reduction from special case to general case. Reduction by encoding with gadgets
Reduction from Special Case to General Case Basic reduction strategies. Reduction by simple equivalence. Reduction from special case to general case. Reduction by encoding with gadgets

Set Cover SET COVER:Given a set U of elements,a collection S1,S2,...,Sm of subsets of U,and an integer k,does there exist a collection of s k of these sets whose union is equal to U? Sample application. m available pieces of software. Set U of n capabilities that we would like our system to have. The ith piece of software provides the set SiU of capabilities. Goal:achieve all n capabilities using fewest pieces of software. Ex: U={1,2,3,4,5,6,7} k=2 51=3,7乃 S4={2,4 52=34,5,6] 55=5} S3={1} S6=1,2,6,7乃 14
14 Set Cover SET COVER: Given a set U of elements, a collection S1 , S2 , . . . , Sm of subsets of U, and an integer k, does there exist a collection of k of these sets whose union is equal to U? Sample application. m available pieces of software. Set U of n capabilities that we would like our system to have. The ith piece of software provides the set Si U of capabilities. Goal: achieve all n capabilities using fewest pieces of software. Ex: U = { 1, 2, 3, 4, 5, 6, 7 } k = 2 S1 = {3, 7} S4 = {2, 4} S2 = {3, 4, 5, 6} S5 = {5} S3 = {1} S6 = {1, 2, 6, 7}
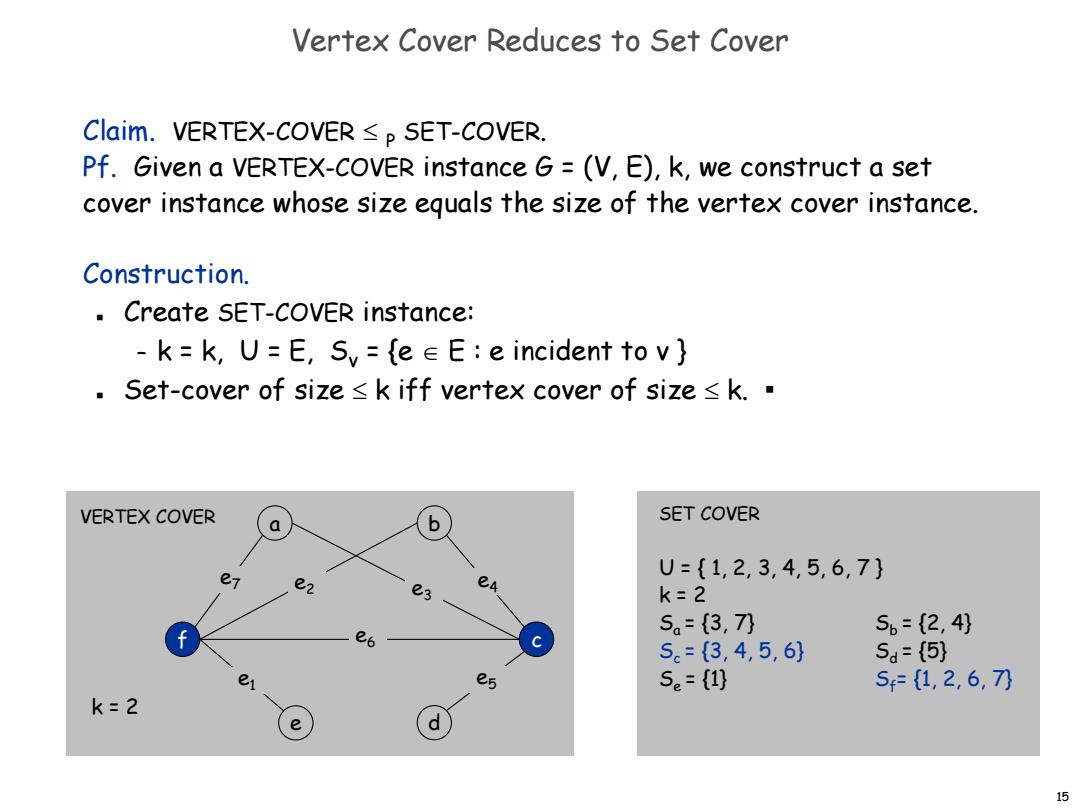
Vertex Cover Reduces to Set Cover Claim.VERTEX-COVER <p SET-COVER. Pf.Given a VERTEX-COVER instance G=(V,E),k,we construct a set cover instance whose size equals the size of the vertex cover instance. Construction. Create SET-COVER instance: -k=k,U=E,Sy=eEE:e incident to v} Set-cover of size <k iff vertex cover of size k. VERTEX COVER 0 b SET COVER e1 U={1,2,3,4,5,6,7} 3 k=2 5a=3,7刀 5b={2,4} 5。=3,4,5,6) 5.=5} 5e=1) 5=1,2,6,7刀 k=2 e d 15
15 SET COVER U = { 1, 2, 3, 4, 5, 6, 7 } k = 2 Sa = {3, 7} Sb = {2, 4} Sc = {3, 4, 5, 6} Sd = {5} Se = {1} Sf= {1, 2, 6, 7} Vertex Cover Reduces to Set Cover Claim. VERTEX-COVER P SET-COVER. Pf. Given a VERTEX-COVER instance G = (V, E), k, we construct a set cover instance whose size equals the size of the vertex cover instance. Construction. Create SET-COVER instance: – k = k, U = E, Sv = {e E : e incident to v } Set-cover of size k iff vertex cover of size k. ▪ a d b e f c VERTEX COVER k = 2 e1 e2 e3 e5 e4 e6 e7