
Polynomial-Time Reduction don't confuse with reduces from Reduction.Problem X polynomial reduces to problem y if arbitrary instances of problem X can be solved using: Polynomial number of standard computational steps,plus Polynomial number of calls to oracle that solves problem y. Notation.X≤py. computational model supplemented by special piece of hardware that solves instances of y in a single step Questions. Any requirement on the input size of y? 6
6 Polynomial-Time Reduction Reduction. Problem X polynomial reduces to problem Y if arbitrary instances of problem X can be solved using: Polynomial number of standard computational steps, plus Polynomial number of calls to oracle that solves problem Y. Notation. X P Y. don't confuse with reduces from computational model supplemented by special piece of hardware that solves instances of Y in a single step Questions. Any requirement on the input size of Y?

Polynomial-Time Reduction Purpose.Classify problems according to relative difficulty. Design algorithms.If X sp y and y can be solved in polynomial-time, then X can also be solved in polynomial time. Establish intractability.If Xsp y and X cannot be solved in polynomial-time,then y cannot be solved in polynomial time. Establish equivalence..IfX≤y and y≤pX,we use notation X≡py. \ up to cost of reduction 7
7 Polynomial-Time Reduction Purpose. Classify problems according to relative difficulty. Design algorithms. If X P Y and Y can be solved in polynomial-time, then X can also be solved in polynomial time. Establish intractability. If X P Y and X cannot be solved in polynomial-time, then Y cannot be solved in polynomial time. Establish equivalence. If X P Y and Y P X, we use notation X P Y. up to cost of reduction

Reduction By Simple Equivalence Basic reduction strategies. Reduction by simple equivalence. Reduction from special case to general case. Reduction by encoding with gadgets
Reduction By Simple Equivalence Basic reduction strategies. Reduction by simple equivalence. Reduction from special case to general case. Reduction by encoding with gadgets
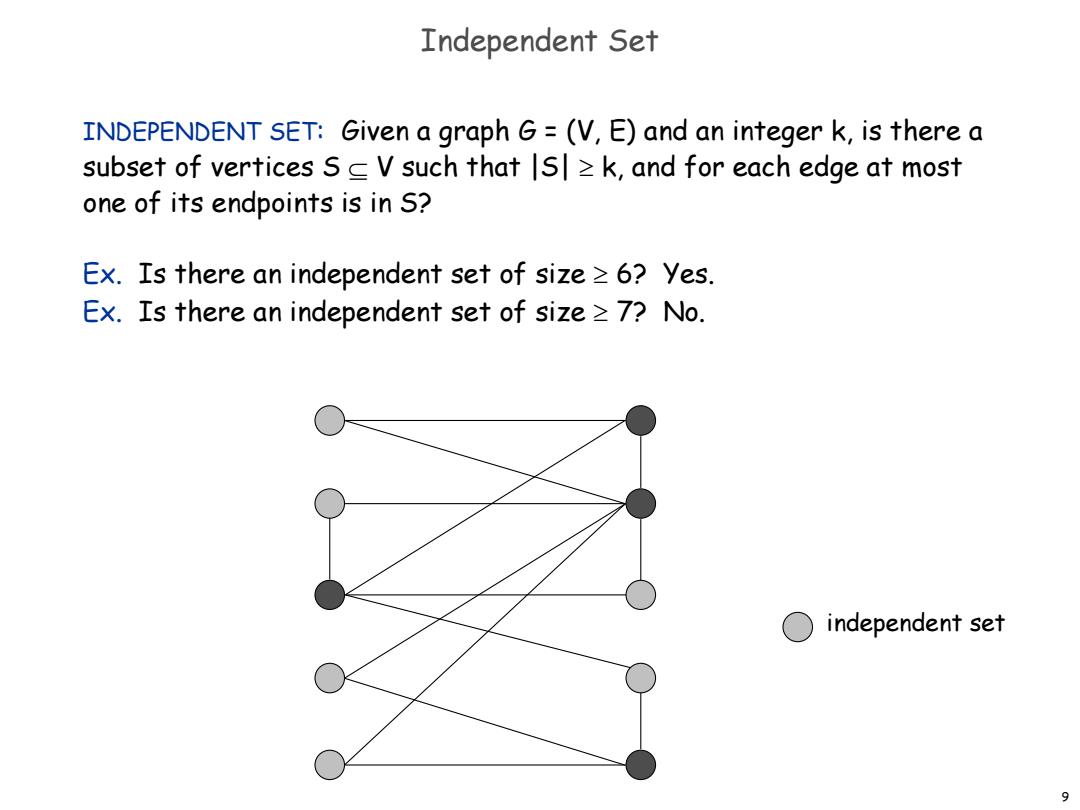
Independent Set INDEPENDENT SET:Given a graph G=(V,E)and an integer k,is there a subset of vertices sc V such that s>k,and for each edge at most one of its endpoints is in S? Ex.Is there an independent set of size≥6?yes. Ex.Is there an independent set of size≥7?No. ○independent set 9
9 Independent Set INDEPENDENT SET: Given a graph G = (V, E) and an integer k, is there a subset of vertices S V such that |S| k, and for each edge at most one of its endpoints is in S? Ex. Is there an independent set of size 6? Yes. Ex. Is there an independent set of size 7? No. independent set

Vertex Cover VERTEX COVER:Given a graph G=(V,E)and an integer k,is there a subset of vertices S V such that ISI s k,and for each edge,at least one of its endpoints is in S? Ex.Is there a vertex cover of size≤4?yes. Ex.Is there a vertex cover of size≤3?No. vertex cover 10
10 Vertex Cover VERTEX COVER: Given a graph G = (V, E) and an integer k, is there a subset of vertices S V such that |S| k, and for each edge, at least one of its endpoints is in S? Ex. Is there a vertex cover of size 4? Yes. Ex. Is there a vertex cover of size 3? No. vertex cover