
Long o HEsh Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Problem o The memory cost and time complexity are at least O(n2)for graph hashing if all pairwise similarities are explicitly computed. oHow to utilize the whole graph and avoid O(n2)complexity? Scalable Graph Hashing(SGH) A feature transformation (Shrivastava and Li,NIPS 2014)method to effectively approximate the whole graph without explicitly computing it. oA sequential method for bit-wise complementary learning. ●Linear complexity. 日卡三4元,互)Q0 Li (http://cs.nju.edu.cn/lvj) Big Leaming CS.NJU 21 /115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Problem The memory cost and time complexity are at least O(n 2 ) for graph hashing if all pairwise similarities are explicitly computed. How to utilize the whole graph and avoid O(n 2 ) complexity? Scalable Graph Hashing(SGH) A feature transformation (Shrivastava and Li, NIPS 2014) method to effectively approximate the whole graph without explicitly computing it. A sequential method for bit-wise complementary learning. Linear complexity. Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 21 / 115

Long o HEsh Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) Objective function minw lles-sgn(K(X)WT)sgn(K(X)WT)T s.t.WK(X)TK(X)WT=I o Vx,define:K(x)= [(x,x1)-∑1p(x,x1)/m,…,(x,xm)-∑=1(xxm)/m 。55=2S-1∈(-1,1. Notation 。X={x1,.,Xn}T∈Rnxd:n data points. 。Pairwise similarity metric defined as::Sj=e-lk-xle/p∈(0,l] 日卡*2元至)Q0 Li (http://cs.nju.edu.cn/lwj) Big Leaming CS.NJU 22 /115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Objective function minW ||cSe − sgn(K(X)WT )sgn(K(X)WT ) T ||2 F s.t. WK(X) T K(X)WT = I ∀x, define: K(x) = [φ(x, x1) − Pn i=1 φ(xi , x1)/n, . . . , φ(x, xm) − Pn i=1 φ(xi , xm)/n] Seij = 2Sij − 1 ∈ (−1, 1]. Notation X = {x1, . . . , xn} T ∈ R n×d : n data points. Pairwise similarity metric defined as: Sij = e −||xi−xj ||2 F /ρ ∈ (0, 1] Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 22 / 115

Long o HEsh Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) oVx,define P(x)and Q(x): -x2 P()-ly 2(e2-1) e2+1-I✉2 e P x;V -e ep e Q(x)-ly 2(e2-1) -llxll e2+1-x e P x V -e ;-1 ep e 0x,xj∈X Pr@)-=4会x+ p 2e 川x喔-区房+2xx 2e -1=S 口卡+得二4元互)Q0 Li (http://cs.nju.edu.cn/lwj) Big Leamning CS.NJU 23/115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) ∀x, define P(x) and Q(x): P(x) = [s 2(e 2 − 1) eρ e −||x||2 F ρ x; r e 2 + 1 e e − ||x||2 F ρ ; 1] Q(x) = [s 2(e 2 − 1) eρ e −||x||2 F ρ x; r e 2 + 1 e e − ||x||2 F ρ ; −1] ∀xi , xj ∈ X P(xi) TQ(xj ) = 2[e 2 − 1 2e × 2x T i xj ρ + e 2 + 1 2e ]e − ||xi ||2 F +||xj ||2 F ρ − 1 ≈ 2e − ||xi ||2 F −||xj ||2 F +2x T i xj ρ − 1 = Seij Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 23 / 115
Loming o HEsh Scalable Graph Hashing with Feature Transformation Feature Transformation 。Here,weuse a approximtion2x+法≈e2 =x+出 0.5 -0.5 0.5 We assume-l≤axx≤l.It is easy to prove that p=2max{lxll2}21 can make-1≤2xxy≤1. Then we have S P(X)TQ(X) 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lvj) Big Leaming CS.NJU 24 /115
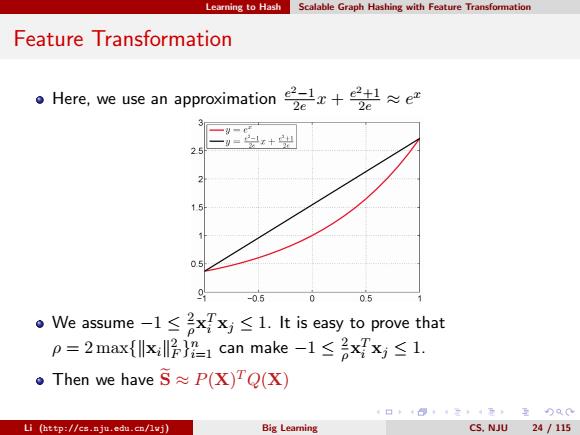
Learning to Hash Scalable Graph Hashing with Feature Transformation Feature Transformation Here, we use an approximation e 2−1 2e x + e 2+1 2e ≈ e x We assume −1 ≤ 2 ρ x T i xj ≤ 1. It is easy to prove that ρ = 2 max{kxik 2 F } n i=1 can make −1 ≤ 2 ρ x T i xj ≤ 1. Then we have Se ≈ P(X) TQ(X) Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 24 / 115

Long o HEsh Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) o Direct relaxation may lead to poor performance.We adopt a sequential learning strategy in a bit-wise complementary manner Residual definition: R:=c5->sgn(K(X)w:)sgn(K(X)w:)T R1=CS oObjective function: min R:-sgn(K(X)w:)sgn(K (X)w:)T s.t.wfK(X)K(X)wt=1 By relaxation,we can get: max tr(wfK(X)R:K(X)wt) We s.t. wK(X)K(X)wt-1 日卡*2元至)Q0 Li (http://cs.nju.edu.cn/lwj) Big Learning C5.NJU25/115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Direct relaxation may lead to poor performance. We adopt a sequential learning strategy in a bit-wise complementary manner Residual definition: Rt = cSe − Pt−1 i=1 sgn(K(X)wi)sgn(K(X)wi) T R1 = cSe Objective function: min wt ||Rt − sgn(K(X)wt)sgn(K(X)wt) T ||2 F s.t. wT t K(X) T K(X)wt = 1 By relaxation, we can get: max wt tr(wT t K(X) T RtK(X)wt) s.t. wT t K(X) T K(X)wt = 1 Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 25 / 115