
Loming o HEsh Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) o Then we obtain a generalized eigenvalue problem: K(X)R:K(X)wt=XK(X)K(X)wt o Key component: cK(X)TSK(X)=cK(X)P(X)Q(X)K(X) =clK(X)P(X)Q(X)K()] Adopting R=cS-sgn(K(X)w:)sgn(K(X)w:)T,we continue the sequential learning procedure. The information in S is fully used,but is not explicitly computed. Time complexity is decreased from O(n2)to O(n). 口卡得三4元互Q0 Li (http://cs.nju.edu.cn/lwj) Big Leamning CS.NJU 26/115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Then we obtain a generalized eigenvalue problem: K(X) T RtK(X)wt = λK(X) T K(X)wt Key component: cK(X) TSeK(X) = cK(X) T P(X) TQ(X) | {z } Se K(X) = c[K(X) TP(X) T ][Q(X)K(X)] Adopting Rt = cSe − Pc i=1,i6=t sgn(K(X)wi)sgn(K(X)wi) T , we continue the sequential learning procedure. The information in Se is fully used, but is not explicitly computed. Time complexity is decreased from O(n 2 ) to O(n). Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 26 / 115

Lemno HEs Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) Algorithm 1 Sequential learning algorithm for SGH Input:Feature vectorsX;code length c:number of kemel bases m. Output:Weight matrix W E Rex m Procedure Construct P(X)and Q(X): Construct K(X)based on the kernel bases.which are m points randomly selected from X: Ao=[K(X)TP(X)HQ(X)K(X)]: A1 =cAo: Z=K(X)TK(X)+Id: for t=1 c do Solve the following generalized eigenvalue problem Atw:=AZwt: U=K(X)sgn(K(X)wt)K(X)Tagn(K(X)w): At+1=A:-U: end for Ao Ac+1 Randomly permutate {1,2,..,c}to generate a random index set M: for 1 c do =M(t): Ao =Ao+K(X)Tsgn(K(X)wi)sgn(K(X)w;)K(X); Solve the following generalized eigenvalue problem Aov =AZv: Update wi+v Ao Ao-K(X)Tsgn(K(X)wi)sgn(K(X)wi)TK(X): end for 口卡+得二4元互)Q0 Li (http://cs.nju.edu.cn/lvj) Big Learning CS.NJU 27 /115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Algorithm 1 Sequential learning algorithm for SGH Input: Feature vectors X ∈ Rn×d; code length c; number of kernel bases m. Output: Weight matrix W ∈ Rc×m. Procedure Construct P (X) and Q(X); Construct K(X) based on the kernel bases, which are m points randomly selected from X; A0 = [K(X) T P (X) T ][Q(X)K(X)]; A1 = cA0; Z = K(X) T K(X) + γId; for t = 1 → c do Solve the following generalized eigenvalue problem Atwt = λZwt; U = [K(X) T sgn(K(X)wt)][K(X) T sgn(K(X)wt)]T ; At+1 = At − U; end for Ac0 = Ac+1 Randomly permutate {1, 2, · · · , c} to generate a random index set M; for t = 1 → c do tˆ = M(t); Ac0 = Ac0 + K(X) T sgn(K(X)wtˆ)sgn(K(X)wtˆ) T K(X); Solve the following generalized eigenvalue problem Ac0v = λZv; Update wtˆ ← v Ac0 = Ac0 − K(X) T sgn(K(X)wtˆ)sgn(K(X)wtˆ) T K(X); end for Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 27 / 115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) Top-1k precision @TINY-1M. Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 0.4697 0.5742 0.6299 0.6737 0.7357 ITQ 0.4289 0.4782 0.4947 0.4986 0.5003 AGH 0.3973 0.4402 0.4577 0.4654 0.4767 DGH-I 0.3974 0.4536 0.4737 0.4874 0.4969 DGH-R 0.3793 0.4554 0.4871 0.4989 0.5276 PCAH 0.2457 0.2203 0.2000 0.1836 0.1421 LSH 0.2507 0.3575 0.4122 0.4529 0.5212 Top-1k precision @MIRFLICKR-1M. Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 0.4919 0.6041 0.6677 0.6985 0.7584 ITQ 0.5177 0.5776 0.5999 0.6096 0.6228 AGH 0.4299 0.4741 0.4911 0.4998 0.506 DGH-I 0.4299 0.4806 0.5001 0.5111 0.5253 DGH-R 0.4121 0.4776 0.5054 0.5196 0.5428 PCAH 0.2720 0.2384 0.2141 0.1950 0.1508 LSH 0.2597 0.3995 0.466 0.5160 0.6072 Li (http://cs.nju.edu.cn/lvj) Big Leaming CS.NJU 28 /115
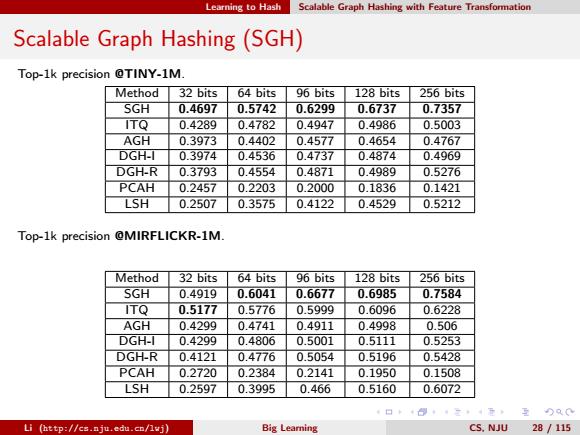
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Top-1k precision @TINY-1M. Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 0.4697 0.5742 0.6299 0.6737 0.7357 ITQ 0.4289 0.4782 0.4947 0.4986 0.5003 AGH 0.3973 0.4402 0.4577 0.4654 0.4767 DGH-I 0.3974 0.4536 0.4737 0.4874 0.4969 DGH-R 0.3793 0.4554 0.4871 0.4989 0.5276 PCAH 0.2457 0.2203 0.2000 0.1836 0.1421 LSH 0.2507 0.3575 0.4122 0.4529 0.5212 Top-1k precision @MIRFLICKR-1M. Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 0.4919 0.6041 0.6677 0.6985 0.7584 ITQ 0.5177 0.5776 0.5999 0.6096 0.6228 AGH 0.4299 0.4741 0.4911 0.4998 0.506 DGH-I 0.4299 0.4806 0.5001 0.5111 0.5253 DGH-R 0.4121 0.4776 0.5054 0.5196 0.5428 PCAH 0.2720 0.2384 0.2141 0.1950 0.1508 LSH 0.2597 0.3995 0.466 0.5160 0.6072 Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 28 / 115
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing(SGH) Training time @TINY-1M.Here,t1 1438.60 Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 34.49 52.37 71.53 89.65 164.23 ITQ 31.72 60.62 89.01 149.18 322.06 AGH 18.60+t1 19.40+t1 20.08+t1 22.48+t1 25.09+t1 DGH-I 187.57+t1 296.99+t1 518.57+t1 924.08+t1 1838.30+t1 DGH-R 217.06+t1 360.18+t1 615.74+t1 1089.10+t1 2300.10+t1 PCAH 4.29 4.54 4.75 5.85 6.49 LSH 1.68 1.77 1.84 2.55 3.76 Training time @MIRFLICKR-1M.Here,t2=1564.86 Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 41.51 59.02 74.86 97.25 168.35 ITQ 36.17 64.61 89.50 132.71 285.10 AGH 17.99+t2 18.80+t2 20.30+t2 19.87+t2 21.60+t2 DGH-I 85.81+t2 143.68+t2 215.41+t2 352.73+t2 739.56+t2 DGH-R 116.25+t2 206.24+t2 308.32+t2 517.97+t2 1199.44+t2 PCAH 7.65 7.90 8.47 9.23 10.42 LSH 2.44 2.43 2.71 3.38 4.21 Li (http://cs.nju.edu.cn/lvj) Big Learing CS.NJU 29/115
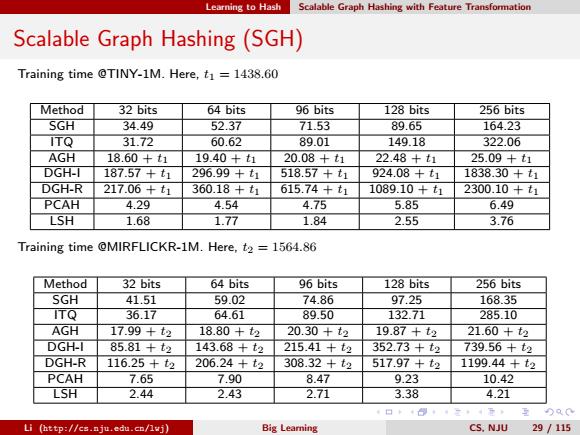
Learning to Hash Scalable Graph Hashing with Feature Transformation Scalable Graph Hashing (SGH) Training time @TINY-1M. Here, t1 = 1438.60 Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 34.49 52.37 71.53 89.65 164.23 ITQ 31.72 60.62 89.01 149.18 322.06 AGH 18.60 + t1 19.40 + t1 20.08 + t1 22.48 + t1 25.09 + t1 DGH-I 187.57 + t1 296.99 + t1 518.57 + t1 924.08 + t1 1838.30 + t1 DGH-R 217.06 + t1 360.18 + t1 615.74 + t1 1089.10 + t1 2300.10 + t1 PCAH 4.29 4.54 4.75 5.85 6.49 LSH 1.68 1.77 1.84 2.55 3.76 Training time @MIRFLICKR-1M. Here, t2 = 1564.86 Method 32 bits 64 bits 96 bits 128 bits 256 bits SGH 41.51 59.02 74.86 97.25 168.35 ITQ 36.17 64.61 89.50 132.71 285.10 AGH 17.99 + t2 18.80 + t2 20.30 + t2 19.87 + t2 21.60 + t2 DGH-I 85.81 + t2 143.68 + t2 215.41 + t2 352.73 + t2 739.56 + t2 DGH-R 116.25 + t2 206.24 + t2 308.32 + t2 517.97 + t2 1199.44 + t2 PCAH 7.65 7.90 8.47 9.23 10.42 LSH 2.44 2.43 2.71 3.38 4.21 Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 29 / 115

Learning to Hash Supervised Hashing with Latent Factor Models Problem Definition Input: Feature vectors:xiRD,i=1,....N. (Compact form:X E RNxD) Similarity labels:sij,i,j=1,...,N. (Compact form:S={sij}) sij=1 if points i and j belong to the same class. sij=0 if points i and j belong to different classes. Output: 。Binary codes:b,∈{-l,1}e,i=1,.,N. (Compact form:BE{-1,1]NxQ) When sij =1,the Hamming distance between bi and bj should be low. When sij =0,the Hamming distance between bi and bj should be high. Li (http://cs.nju.edu.cn/lwj) Big Leaming CS.NJU 30/115
Learning to Hash Supervised Hashing with Latent Factor Models Problem Definition Input: Feature vectors: xi ∈ R D, i = 1, . . . , N. (Compact form: X ∈ R N×D) Similarity labels: sij , i, j = 1, . . . , N. (Compact form: S = {sij}) sij = 1 if points i and j belong to the same class. sij = 0 if points i and j belong to different classes. Output: Binary codes: bi ∈ {−1, 1} Q, i = 1, . . . , N. (Compact form: B ∈ {−1, 1} N×Q) When sij = 1, the Hamming distance between bi and bj should be low. When sij = 0, the Hamming distance between bi and bj should be high. Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 30 / 115