
Learning to Hash Isotropic Hashing Motivation Problem: All existing methods use the same number of bits for different projected dimensions with different variances. PCA2 PCAI XX ◆X Possible Solutions: oDifferent number of bits for different dimensions (Variable bit quantization (Moran et al,ACL 2013)) o Isotropic (equal)variances for all dimensions Li (http://cs.nju.edu.cn/lwj) Big Leaming CS.NJU 16/115
Learning to Hash Isotropic Hashing Motivation Problem: All existing methods use the same number of bits for different projected dimensions with different variances. Possible Solutions: Different number of bits for different dimensions (Variable bit quantization (Moran et al, ACL 2013)) Isotropic (equal) variances for all dimensions Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 16 / 115

Learning to Hash Isotropic Hashing PCA Hash To generate a code of m bits,PCAH performs PCA on X,and then use the top m eigenvectors of the matrixXXT as columns of the projection matrix W ERdxm.Here,top m eigenvectors are those corresponding to the m largest eigenvalues generally arranged with the non-increasing order1≥2≥…≥入m.LetA=[d,2,…,入mJT. Then A=WTXXTW diag(A) Define hash function h(x)=sgn(WTx) 日卡三4元,互)Q0 Li (http://cs.nju.edu.cn/lwj) Big Leamning CS.NJU 17/115
Learning to Hash Isotropic Hashing PCA Hash To generate a code of m bits, PCAH performs PCA on X, and then use the top m eigenvectors of the matrix XXT as columns of the projection matrix W ∈ R d×m. Here, top m eigenvectors are those corresponding to the m largest eigenvalues {λk} m k=1, generally arranged with the non-increasing order λ1 ≥ λ2 ≥ · · · ≥ λm. Let λ = [λ1, λ2, · · · , λm] T . Then Λ = WT XXTW = diag(λ) Define hash function h(x) = sgn(WT x) Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 17 / 115

Learning to Hash Isotropic Hashing Idea of IsoHash Learn an orthogonal matrix QE Rmxm which makes QTWTXXTWQ become a matrix with equal diagonal values. oEffect of Q:to make each projected dimension have the same variance while keeping the Euclidean distances between any two points unchanged. 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lwj) Big Leaming CS.NJU 18/115
Learning to Hash Isotropic Hashing Idea of IsoHash Learn an orthogonal matrix Q ∈ R m×m which makes QTWT XXTW Q become a matrix with equal diagonal values. Effect of Q: to make each projected dimension have the same variance while keeping the Euclidean distances between any two points unchanged. Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 18 / 115
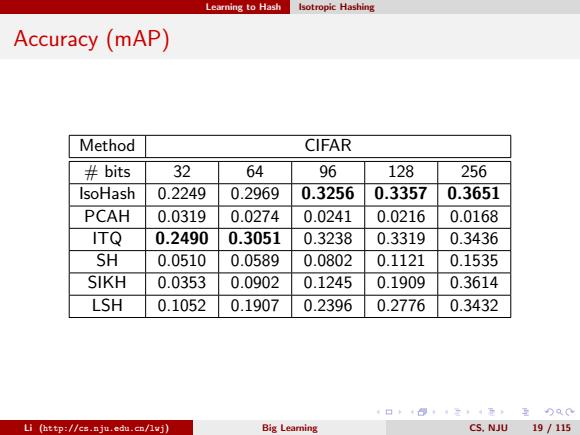
Learning to Hash Isotropic Hashing Accuracy(mAP) Method CIFAR #bits 32 64 96 128 256 IsoHash 0.2249 0.2969 0.3256 0.3357 0.3651 PCAH 0.0319 0.0274 0.0241 0.0216 0.0168 ITQ 0.2490 0.3051 0.3238 0.3319 0.3436 SH 0.0510 0.0589 0.0802 0.1121 0.1535 SIKH 0.0353 0.0902 0.1245 0.1909 0.3614 LSH 0.1052 0.1907 0.2396 0.2776 0.3432 4日卡0,·三·4元至)及0 Li (http://cs.nju.edu.cn/lvj) Big Learning CS.NJU 19/115
Learning to Hash Isotropic Hashing Accuracy (mAP) Method CIFAR # bits 32 64 96 128 256 IsoHash 0.2249 0.2969 0.3256 0.3357 0.3651 PCAH 0.0319 0.0274 0.0241 0.0216 0.0168 ITQ 0.2490 0.3051 0.3238 0.3319 0.3436 SH 0.0510 0.0589 0.0802 0.1121 0.1535 SIKH 0.0353 0.0902 0.1245 0.1909 0.3614 LSH 0.1052 0.1907 0.2396 0.2776 0.3432 Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 19 / 115
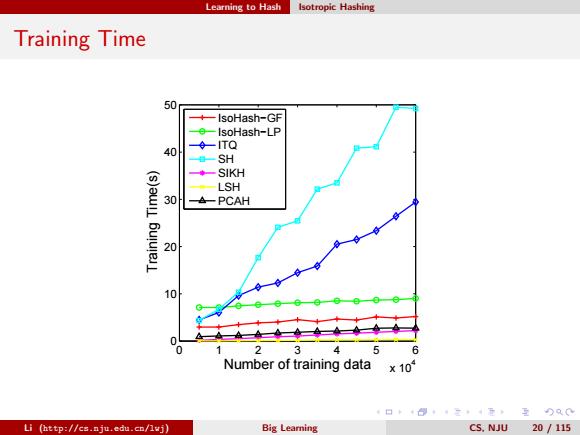
Learning to Hash Isotropic Hashing Training Time 50 IsoHash-GF IsoHash-LP --ITQ 40 SH ◆-SKH LSH 30 -PCAH 20 10 0 2 3 5 6 Number of training data x 10 口卡+得,二4元互)Q0 Li (http://cs.nju.edu.cn/lvj) Big Leamning CS.NJU 20 /115
Learning to Hash Isotropic Hashing Training Time 0 1 2 3 4 5 6 x 104 0 10 20 30 40 50 Number of training data Training Time(s) IsoHash−GF IsoHash−LP ITQ SH SIKH LSH PCAH Li (http://cs.nju.edu.cn/lwj) Big Learning CS, NJU 20 / 115