
§1.2.1主应力及应力张量不变量 主应力(Principal stress):指作用面上无切应力时 所对应的正应力,该作用面称作主平面,法线方向为主轴或 主方向 设主应力为0,当为主广 时, S.=al,S,=oly S.=al. 有 代入整理,有 (ox-o)儿+tn,+t.=0 该面叫做主平面, T+(o,-o)儿,+t3=0 法线方向为主方向 tE+t,+(o-o)1,=0 求解1x、1y、1,的非零解,必有系数行列式值为零,最终 可得:
§1.2.1 主应力及应力张量不变量 主应力(Principal stress ):指作用面上无切应力时 所对应的正应力,该作用面称作主平面,法线方向为主轴或 主方向 设主应力为σ,当为主方向时, 有 , , ,代入整理,有: x x S l = S l y y = z z S l = + + − = + − + = − + + = ( ) 0 ( ) 0 ( ) 0 xz x yz y z z xy x y y z y z x x yx y z x z l l l l l l l l l 求解lx、ly、lz的非零解,必有系数行列式值为零,最终 可得 : 该面叫做主平面, 法线方向为主方向

工、I2、I称作应力 o3-1o2-120-13=0 张量的第一、二、三 不变量。 式中 11=0x+0,+0=01+02+03 12= 6 6 =O0,+0,0+00x-T =0102+0203+g301 69 13= =010203
= 1 2 3 z y yz x xy xz I . . . 3 = 1 2 2 3 3 1 2 2 2 = + + = x y + y z + z x − xy − yz − z x xz x z z x z y z y yz yx y x xy I 2 = + + 1 = x + y + z = 1 + 2 + 3 式中 I 2 3 0 2 1 3 − I − I − I = I 1 、 I 2 、 I 3称作应力 张量的第一、二、三 不变量

>讨论: 1.可以证明,在应力空间,主应力平面是存在的 2.三个主平面是相互正交的: 3.三个主应力均为实根,不可能为虚根; 4.应力特征方程的解是唯一的: 5.对于给定的应力状态,应力不变量也具有唯一性: 6.应力第一不变量I,反映变形体体积变形的剧烈程 度,与塑性变形无关;I3也与塑性变形无关冫I2与塑性 变形无关。 7.应力不变量不随坐标而改变,是点的确定性的判据
➢ 讨论: 1. 可以证明,在应力空间,主应力平面是存在的; 2. 三个主平面是相互正交的; 3. 三个主应力均为实根,不可能为虚根; 4. 应力特征方程的解是唯一的; 5. 对于给定的应力状态,应力不变量也具有唯一性; 6. 应力第一不变量I1反映变形体体积变形的剧烈程 度,与塑性变形无关;I3也与塑性变形无关;I2与塑性 变形无关。 7. 应力不变量不随坐标而改变,是点的确定性的判据
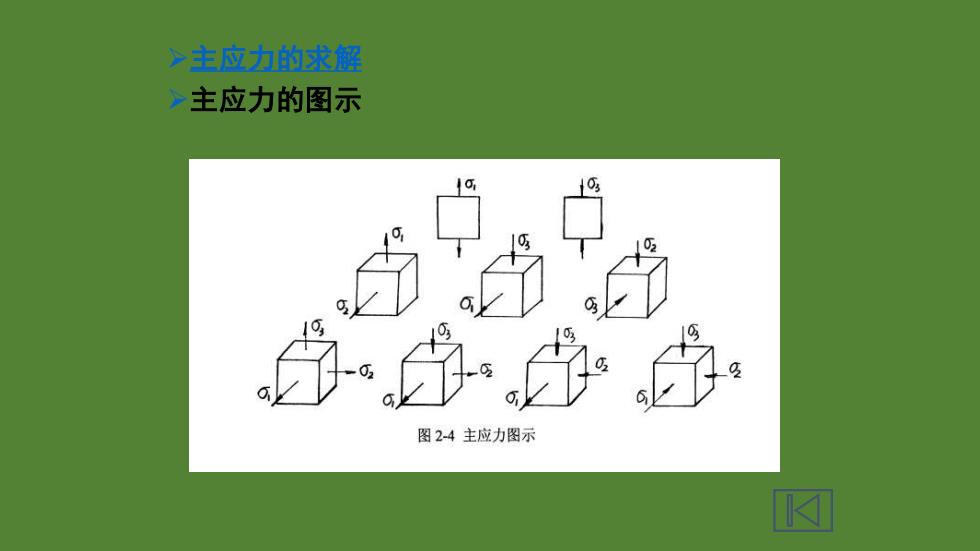
一主应力的求解 ,主应力的图示 图2-4主应力图示
➢主应力的求解 ➢主应力的图示

§1.2.2主切应力和最大剪切应力 一主切应力(Principal shear stress).:极值切应力(不为零】 平面上作用的切应力。 >最大剪应力(Maximun shee stress): 主应力空间的{110} 面族 通常规定:0,≥0≥0 则有最大剪应力 =01-03 2 或者:Tnax=maxt2br2alta 其中: 2 2 2 且有: T12+T23+T31=0
§1.2.2 主切应力和最大剪切应力 ➢主切应力(Principal shear stress):极值切应力(不为零) 平面上作用的切应力。 ➢最大剪应力(Maximun shear stress): 通常规定: 1 2 3 2 1 3 max − 则有最大剪应力: = 或者: 其中: 且有: 0 2 , 2 , 2 max{ , , } 12 23 31 3 1 31 2 3 23 1 2 12 max 12 23 31 + + = − = ± − = ± − = ± = 主应力空间的{110}面族