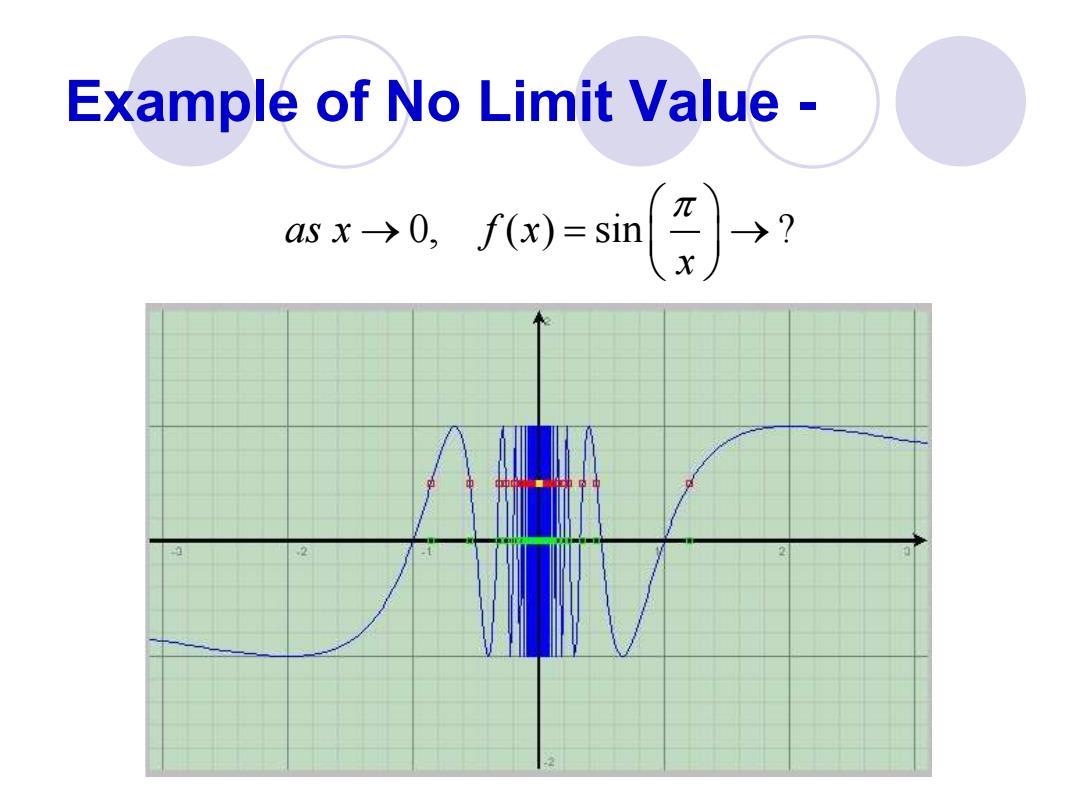
Example of No Limit Value- asx→0,fx)=sin
Example of No Limit Value - as x f x 0, ( ) sin ? x → = →
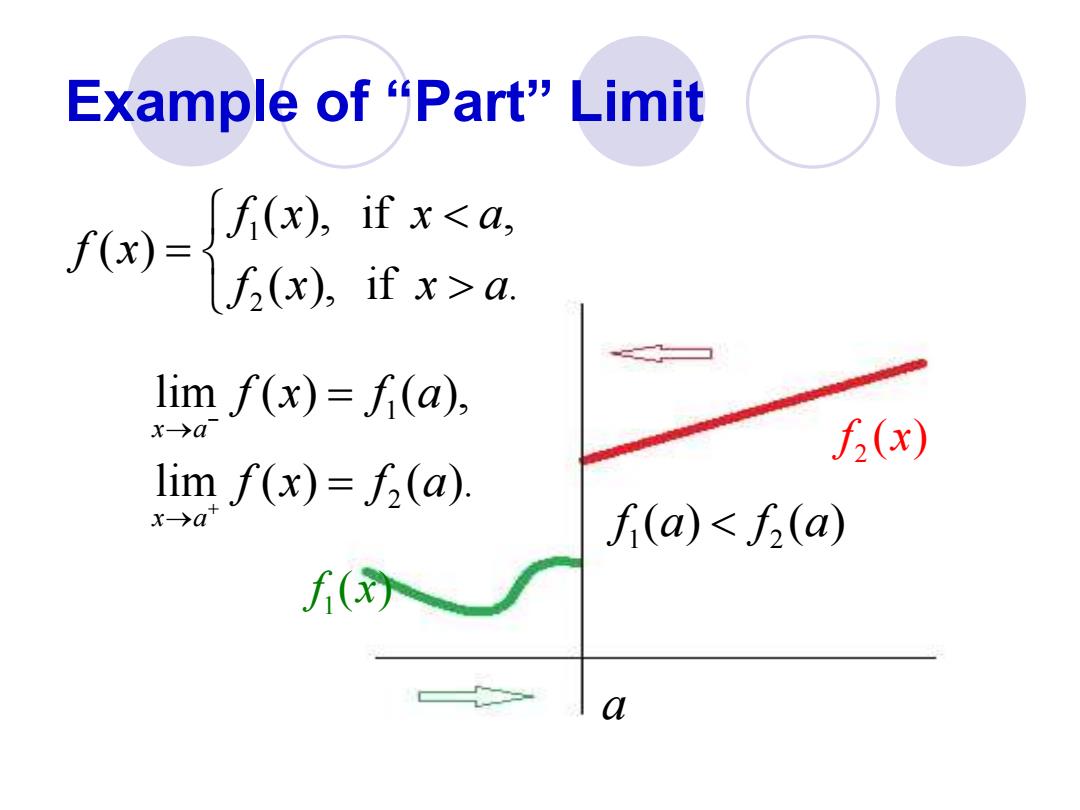
Example of“Part”Limit f(x)= f(x),if x<a, f(x),if x>a. lim f(x)=f(a), f2(x) lim f(x)=f (a) f(a)<f(a) f(
Example of “Part” Limit a 1 2 ( ), if , ( ) ( ), if . f x x a f x f x x a = 1 2 lim ( ) ( ), lim ( ) ( ). x a x a f x f a f x f a − + → → = = 1 f x( ) 2 f x( ) 1 2 f a f a ( ) ( )

One Side Limit (An Informal View) If the values of f(x)can be made as close as we like to L by taking values of x sufficiently close to a (but greater than a), written as lim f(x)=L x→a ● If the values of f(x)can be made as close as we like to L by taking values of x sufficiently close to a (but less than a), written as lim f(x)=L x->a
One Side Limit (An Informal View) ⚫If the values of f (x) can be made as close as we like to L by taking values of x sufficiently close to a (but greater than a), written as ⚫ If the values of f (x) can be made as close as we like to L by taking values of x sufficiently close to a (but less than a), written as lim ( ) x a f x L → + = lim ( ) x a f x L → − =

Example unequal 2-sided limit lim not exists, x-→0 X lim lx=lim¥=l≠imX=limx=-l x→0*X x→0X x→0X x-→0X
Example unequal 2-sided limit 0 0 0 0 0 | | lim not exists, | | | | lim lim 1 lim lim 1 x x x x x x x x x x x x x x x + − → → → → → − = = = = − 1 -1

Infinite Limit(An Informal View) If the values of f(x)increases without bound as x approaches a from left or right or both,written as respectively lim f(x)=+0,lim f(x)=+0,lim f(x)=+oo X→d x→a oIf the values of f(x)decreases without bound as x approaches a from left or right or both,written as respectively lim f(x)=-0,lim f(x)=-0,limf(x)=- X->0
Infinite Limit (An Informal View) ⚫If the values of f (x) increases without bound as x approaches a from left or right or both, written as respectively ⚫If the values of f (x) decreases without bound as x approaches a from left or right or both, written as respectively lim ( ) , lim ( ) , lim ( ) x a x a x a f x f x f x → → − + → = + = + = + lim ( ) , lim ( ) , lim ( ) x a x a x a f x f x f x → → − + → = − = − = −