
Chapter Two Limits Continuity
Chapter Two Limits & Continuity
Enter Calculus World ●Ve have known“Function” o This is the tool for us enter the Calculus World ●The first adventure is“Limit” o Limits is the soul of Calculus as well as "Advanced Mathematics"!
Enter Calculus World ⚫We have known “Function” ⚫This is the tool for us enter the Calculus World ⚫The first adventure is “Limit” ⚫Limits is the soul of Calculus as well as “Advanced Mathematics”!

Ancient Limit Thought ● Zhuangzi(庄子,369-286B.C) in《天下》said: ○一尺之锤,日取其半,万世不竭。 o Chinese ancient mathematician Liu Hui(刘徽)in263a.c.said in《九章算术》 ○“割之弥细,所失弥小.割之又割, 以至于不可割,则与圆周合体,而无 所失矣
Ancient Limit Thought ⚫ Zhuangzi (庄子,369-286 B.C) in《天下》said: 一尺之锤,日取其半,万世不竭。 ⚫ Chinese ancient mathematician Liu Hui (刘徽) in 263 a.c. said in《九章算术》 : “割之弥细,所失弥小. 割之又割, 以至于不可割,则与圆周合体,而无 所失矣
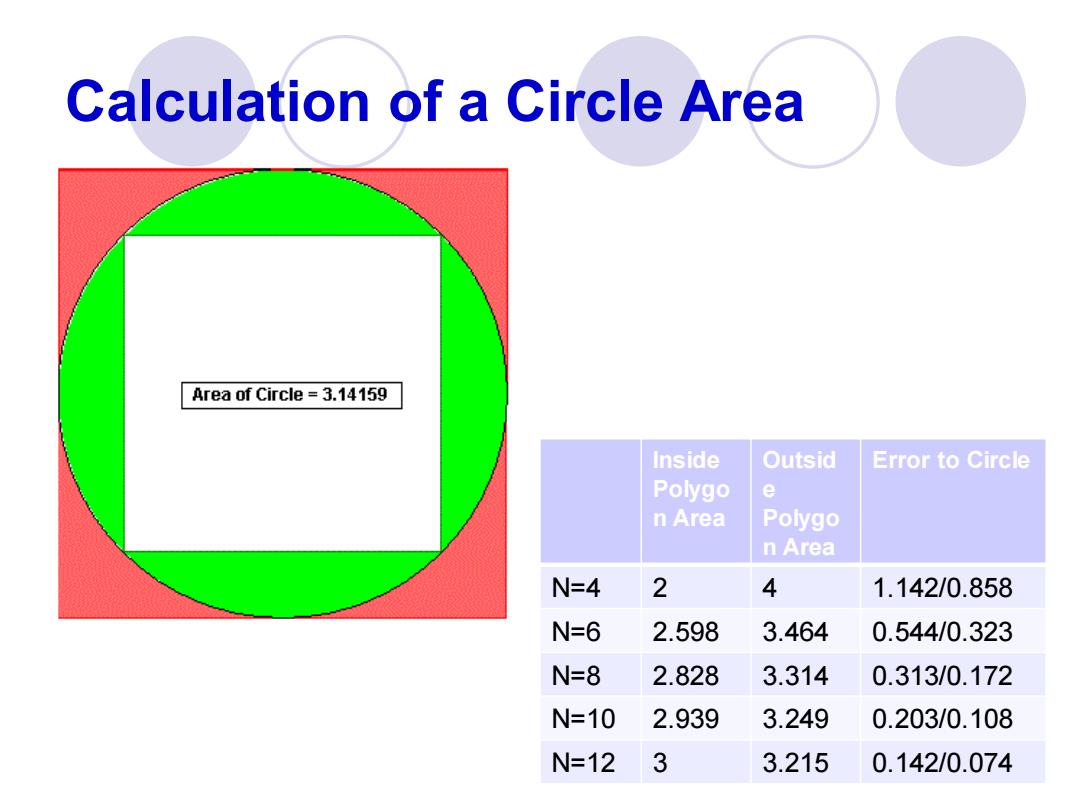
Calculation of a Circle Area Area of Circle =3.14159 Inside Outsid Error to Circle Polygo e n Area Polygo n Area N=4 2 4 1.142/0.858 N=6 2.598 3.464 0.544/0.323 N=8 2.828 3.314 0.313/0.172 N=10 2.939 3.249 0.203/0.108 N=123 3.215 0.142/0.074
Inside Polygo n Area Outsid e Polygo n Area Error to Circle N=4 2 4 1.142/0.858 N=6 2.598 3.464 0.544/0.323 N=8 2.828 3.314 0.313/0.172 N=10 2.939 3.249 0.203/0.108 N=12 3 3.215 0.142/0.074 Calculation of a Circle Area

Zeno of Elea (490-430 BC) paradoxes- O Achilles and the Tortoise OA is in a footrace with a slow T by 10*its speed. OA allows T a head start of 100 meters. OAfter A run 100 m,to T start point,meanwhile,T run 10 m. OA then run 10 m,and T has advanced farther; OA need more time to reach 3rd point,while T moves ahead. O Thus,whenever A reaches somewhere T has been,he still has farther to go.Therefore,as there are an infinite number of points A must reach where T has already been,he never overtake T
Zeno of Elea (490–430 BC) paradoxes- ⚫ Achilles and the Tortoise : A is in a footrace with a slow T by 10* its speed. A allows T a head start of 100 meters. After A run 100 m, to T start point, meanwhile, T run 10 m. A then run 10 m, and T has advanced farther; A need more time to reach 3rd point, while T moves ahead. Thus, whenever A reaches somewhere T has been, he still has farther to go. Therefore, as there are an infinite number of points A must reach where T has already been, he never overtake T