电子科技大学：《光波导理论与技术 Optical Waveguides Principles and Technologies》课程教学资源（课件讲稿）第二章 平板光波导——结构与分析

University of Electronic Science and Technology of China 1.平板光波导的几何光学分析 1956 模式本征方程的导出-方法二 侧视图 图2-9.平 板波导的 n3 传输特征 n2 基底 平面波的波数：k=nk,k,=2π/2 (2-8) 波矢量沿z方向的分量：B=kn1sina (2-9) 波矢量沿x方向的分量：k.=±kn1C0sa (2-10) 16

University of Electronic Science and Technology of China 16 ➢ 模式本征方程的导出-方法二 图 2-9. 平 板波导的 传输特征 ▪ 平面波的波数： k = n1 k0 , k0 = 2  ▪ 波矢量沿z方向的分量：  = k0 n1 sin ▪ 波矢量沿x方向的分量： (2-10) (2-8) kx = k0 n1 cos (2-9) 侧视图 基底  h n2 n3 n1 x z k  kx  kx k 1. 平板光波导的几何光学分析

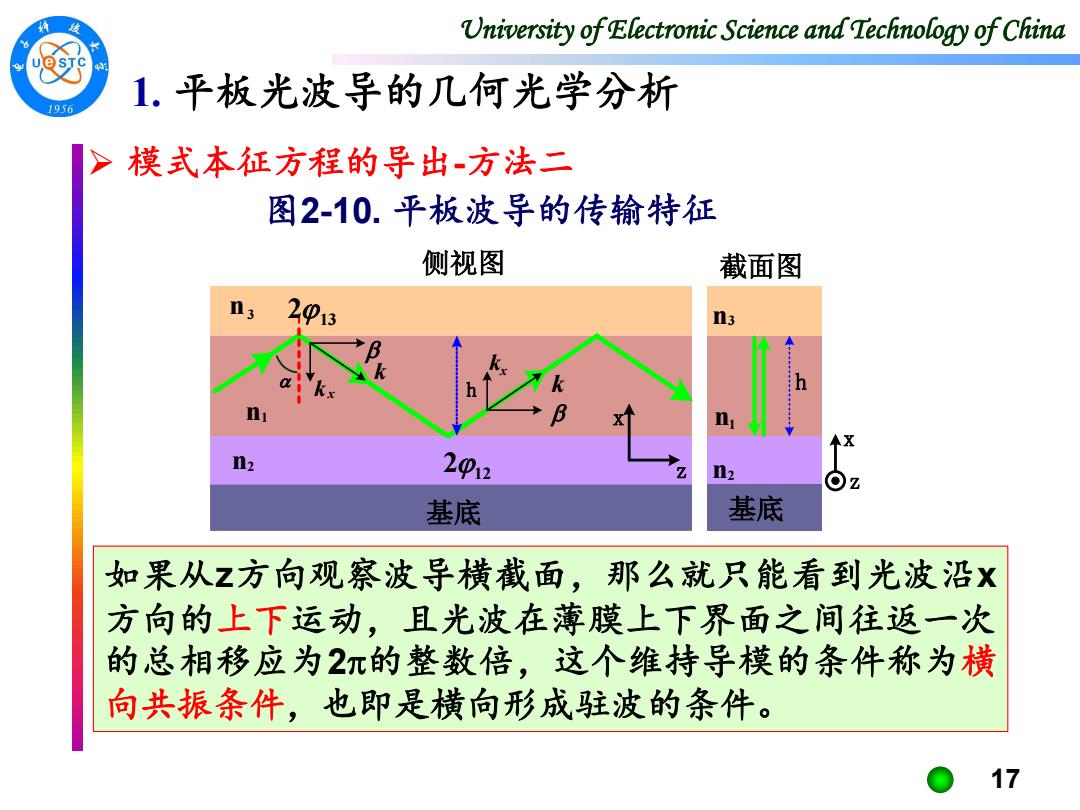
University of Electronic Science and Technology of China 1.平板光波导的几何光学分析 1956 模式本征方程的导出-方法二 图2-10.平板波导的传输特征 侧视图 截面图 n; 24013 n3 n2 2012 n2 基底 基底 如果从z方向观察波导横截面，那么就只能看到光波沿X 方向的上下运动，且光波在薄膜上下界面之间往返一次 的总相移应为2π的整数倍，这个维持导模的条件称为横 向共振条件，也即是横向形成驻波的条件。 17

University of Electronic Science and Technology of China 17 ➢ 模式本征方程的导出-方法二 图2-10. 平板波导的传输特征 截面图 基底 x z n2 n1 n3 h 侧视图 基底  h n2 n3 n1 x z k  kx k 213 212 kx  如果从z方向观察波导横截面，那么就只能看到光波沿x 方向的上下运动，且光波在薄膜上下界面之间往返一次 的总相移应为2的整数倍，这个维持导模的条件称为横 向共振条件，也即是横向形成驻波的条件。 1. 平板光波导的几何光学分析

University of Electronic Science and Technology of China X 1.平板光波导的几何光学分析 1956 模式本征方程的导出-方法二 图2-10.平板波导的传输特征 侧视图 截面图 n3 2013 n3 n2 2012 Z n2 Oz 基底 基底 根据以上分析及图2-10有： kx(2h)-2p12-2p13=2m元 (2-11) 18

University of Electronic Science and Technology of China 18 ➢ 模式本征方程的导出-方法二 图2-10. 平板波导的传输特征 kx (2h) − 212 − 213 = 2m (2-11) 根据以上分析及图2-10有： 1. 平板光波导的几何光学分析 截面图 基底 x z n2 n1 n3 h 侧视图 基底  h n2 n3 n1 x z k  kx k 213 212 kx 

University of Electronic Science and Technology of China 1.平板光波导的几何光学分析 1956 模式本征方程-讨论 在模式本征方程2-7或2-11中，对确定的平板波导（厚 度、材料折射率均确定)，若m确定，则a与p的值是确 定的，其中0依赖于及光波的偏振态。这说明： 只有某些特定的光线传播路径可以稳定地在波导内传输， 这些光线路径称为波导模式（几何光学)。 19

University of Electronic Science and Technology of China 19 ➢ 模式本征方程-讨论 在模式本征方程2-7或2-11中，对确定的平板波导（厚 度、材料折射率均确定），若m确定，则与的值是确 定的，其中 依赖于及光波的偏振态。这说明： 只有某些特定的光线传播路径可以稳定地在波导内传输， 这些光线路径称为波导模式（几何光学）。 1. 平板光波导的几何光学分析

University of Electronic Science and Technology of China 1.平板光波导的几何光学分析 1956 模式本征方程-讨论 在平板波导的模式本征方程 k.(2h)-2012-2p13=2m元 (2-11) 中，m称为模的阶次，取以0开始的有限个正整数，令： kx =tkom cosa=kim(1-sin'a)=/kin-B2 (2-12) 从而2-11式可改写为 kon -B'h=9n +ois +ma (2-13) 20

University of Electronic Science and Technology of China 20 ➢ 模式本征方程-讨论 k n −  h = 12 +13 + m 2 2 1 2 0 (2-12) 中，m称为模的阶次，取以0开始的有限个正整数，令： 从而2-11式可改写为 2 2 1 2 0 2 2 1 2 0 1 0 kx = k n cos = k n (1− sin ) = k n −  (2-13) kx (2h) − 212 − 213 = 2m (2-11) 在平板波导的模式本征方程 1. 平板光波导的几何光学分析