两种反应物的情形 CBO b aA+bB→产物 任意时刻都有2=b CAO a CA a 速率方程为 dc b 1 dcA=kccB dt ake?=bkc=kgc? a b a dt akci=bkcg=kcg dt a aA+bB+.→产物 推广 4=kc骨c哈,若令- b =…,则 dt a des=kaca dt 2024-5-26 16
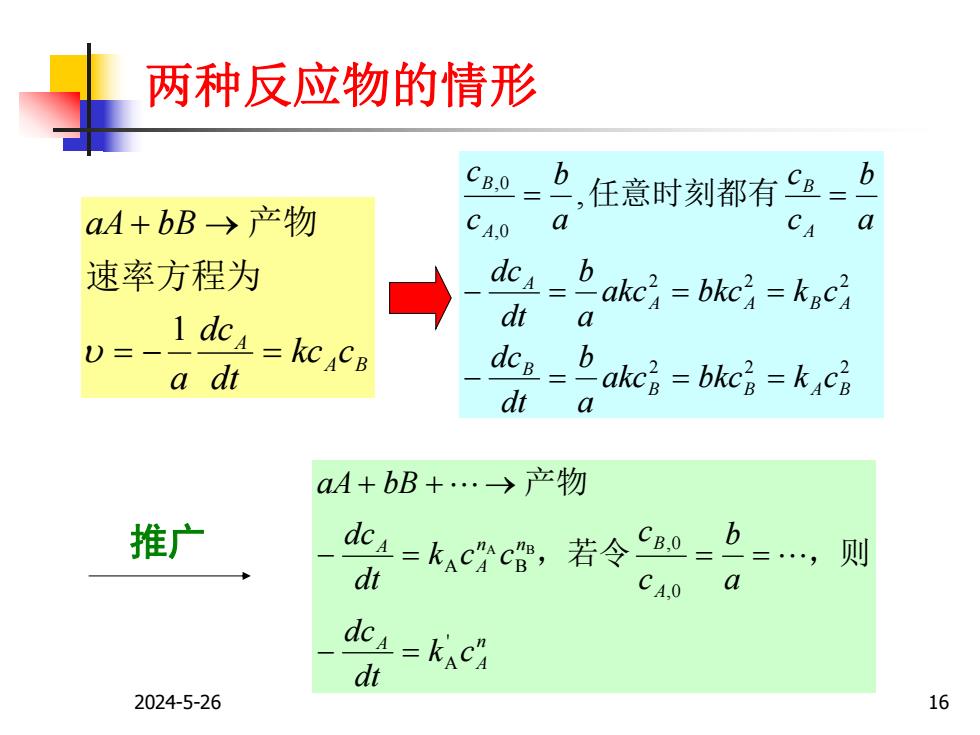
两种反应物的情形 A B A kc c dt dc a aA bB 1 速率方程为 产物 2 2 2 2 2 2 ,0 ,0 , B B A B B A A B A A A B A B akc bkc k c a b dt dc akc bkc k c a b dt dc a b c c a b c c 任意时刻都有 推广 n A A A n n B A A k c dt dc a b c c k c c dt dc aA bB 'A ,0 ,0 A B A B ,若令 ,则 产物 2024-5-26 16

两种反应物的情形 C≠b,任意时刻A,B的消耗量都有CA0-C4=? b CAO a CB.o-CB b =ake,ab-abe) dt In CB/CBo -kt acB.0-bCA.0 CA/CA.O b 令c,=cn-c4,则c4=can-c,cm=6a0a 1 In Cacpo-bekt acB.0 bCAO acB.o(CAo-Cs) 2024-5-26 17
两种反应物的情形 kt c c c c ac bc akc a bc c a bc dt dc b a c c c c A B a b c c A B B B A A B A B B A A B A,0 ,0 ,0 A,0 A,0 1 ,0 1 ,0 A,0 ,0 ,0 ln 1 - ,任意时刻 , 的消耗量都有 kt ac c c c ac bc ac bc c a b c c c c c c c c x x B x A A x x B,0 A,0 A,0 B,0 ,0 A,0 A,0 A,0 B B,0 ln 1 令 ,则 , 2024-5-26 17

n级反应 aA>产物 或反应物浓度符合化学计量比的反应 aA+bB+…·→产物 dt cn 银w中女动体如m八- 2n-1-1 半衰期2=-)k,c 2024-5-26 18
1 ,0 1 1 2 1 1 3 1 1 1 0 1 2 1 1 1 1 1 ,0 ,0 n A A n n n n A t A c c n n A A A n k c t k t k m mol s n c c k dt c dc k c dt dc aA bB aA A A A A A A 半衰期 积分 单位 产物 或反应物浓度符合化学 计量比的反应 产物 n 级反应 2024-5-26 18

速率方程的确定 aA+bB→产物 dck b dt dt CA =kc"k a k4,n4和nB为反应分级数;反应总级数n=n4+nB a 求n令c40<CB,0 确定反应级数 dek-kc 先测量C4一关系 →n,k 求nB令CB.0<C40 dt 2024-5-26 19
速率方程的确定 A A B A B n n n A n A n n c a c b A A A k n n n n n a b k c kc a b k c dt dc k c c dt dc aA bB B A A B A A B A B B A A 和 为反应分级数 反应总级数 产物 , ; / / n k c t A , 先测量 关系 确定反应级数 A A A A B B n A n n A A A A B k c c k c dt dc n c c ' ,0 ,0 ,0 , 求 ,令 B B B B A A n B n n B B B B A k c c k c dt dc n c c ' ,0 ,0 ,0 , 求 ,令 2024-5-26 19

尝试法 四又称试差法:看化学反应的c4与间的关系适 合哪一级数的动力学积分式,从而确定反应级 数。 四代入法:以c4与数据用积分式计算值,若 值为常数,则可确定反应级数。 四作图法:作nc4和n不同时的1/c4-1图, 若成直线,可确定反应级数。 2024-5-26 20
尝试法 &又称试差法:看化学反应的cA与t间的关系适 合哪一级数的动力学积分式,从而确定反应级 数。 &代入法:以cA与t数据用积分式计算k值,若 k值为常数,则可确定反应级数。 &作图法:作lncA-t和n不同时的1/cA n-1-t图, 若成直线,可确定反应级数。 2024-5-26 20