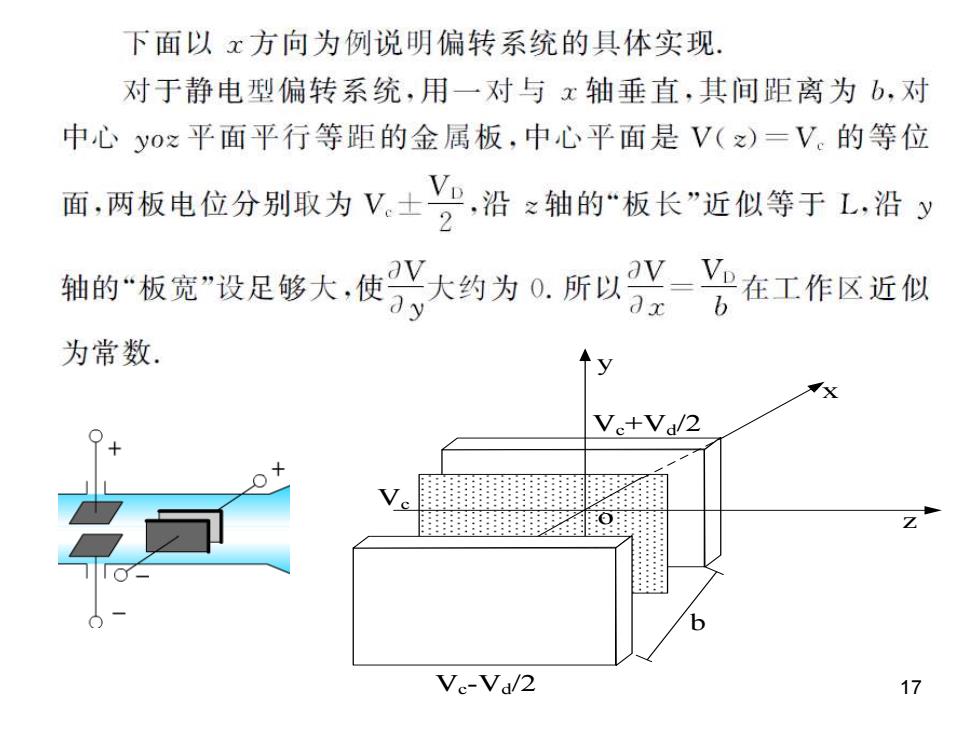
下面以x方向为例说明偏转系统的具体实现 对于静电型偏转系统,用一对与x轴垂直,其间距离为b,对 中心yoz平面平行等距的金属板,中心平面是V(x)=V。的等位 面,两板电位分别取为V士沿轴的“板长”近似等于L沿y 辅的板宽”设足够大,使大约为心所以公在工作风近似 为常数. Ve+Va/2 Ve-Va/2 17
17z y x o Vc Vc+Vd/2 Vc-Vd/2 b
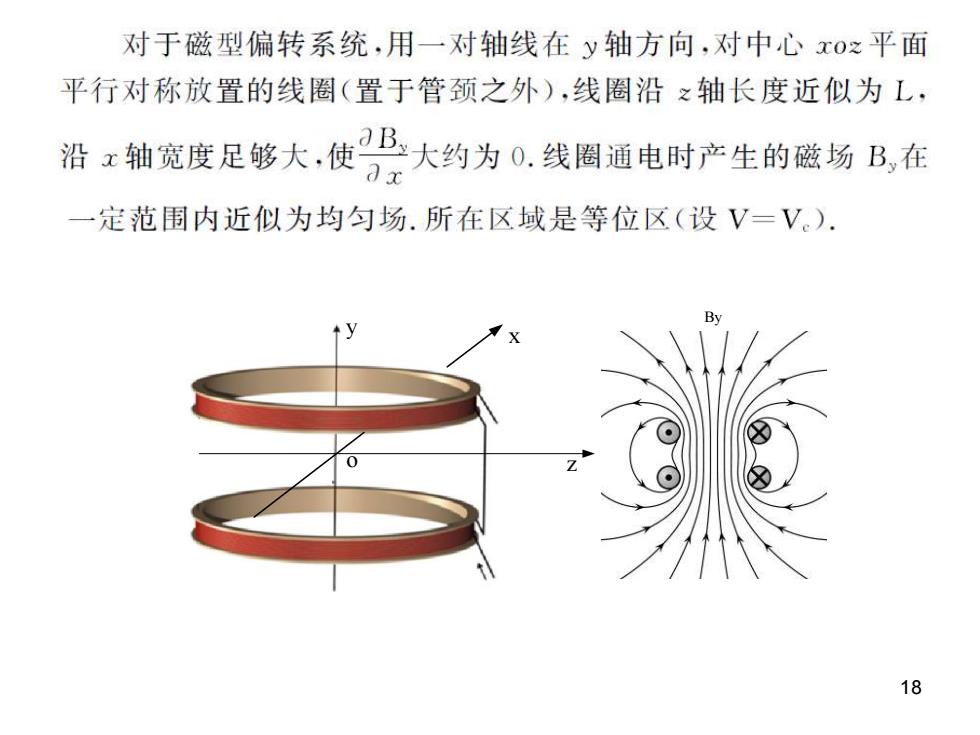
对于磁型偏转系统,用一对轴线在y轴方向,对中心x0之平面 平行对称放置的线圈(置于管颈之外),线圈沿Σ轴长度近似为L, 沿z轴宽度足够大,使B大约为0.线圈通电时产生的磁场B布 一定范围内近似为均匀场.所在区域是等位区(设V=V). 18
18 z y x o By

以上安排皆使G近似满足场的“区间常数假设”,可认为它在 工作区内为常数,在工作区界面上则“突降”至0.检视可知,至少 在工作区内该假设并不违反拉氏方程.而当分析偏转像差问题或 考虑界面附近的“边缘场”,以修正计算结果时,要引入V,B,或B 的更高阶微商,以描述“实际场”,就必须考虑拉氏方程对场的高阶 微商的限制 实用的电子束偏转系统大多有两套,分司水平、垂直两个方向 的偏转.因空间限制,即间距b不可能太大,两套静电偏转板大多 先后错开:而两套磁偏转线圈的工作区可以重叠.当只分析线性偏 转时,无论何种布置,其结果均可叠加,故总可认为两个方向相互 独立. 磁环 行偏转线圖 19 场偏转线圈
19