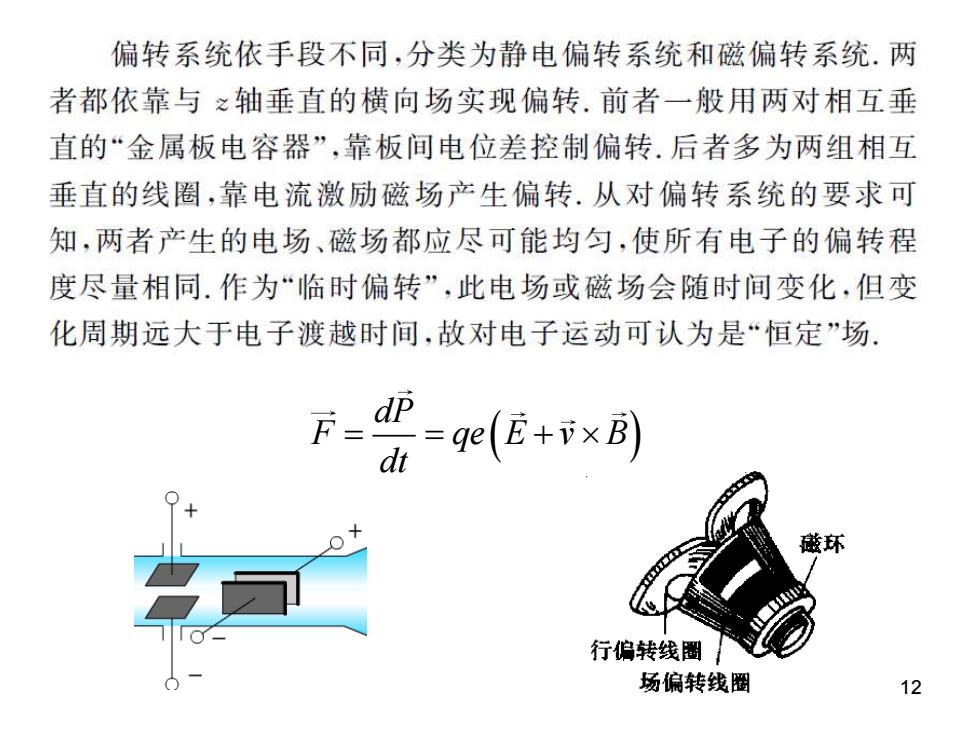
偏转系统依手段不同,分类为静电偏转系统和磁偏转系统.两 者都依靠与之轴垂直的横向场实现偏转.前者一般用两对相互垂 直的“金属板电容器”,靠板间电位差控制偏转.后者多为两组相互 垂直的线圈,靠电流激励磁场产生偏转.从对偏转系统的要求可 知,两者产生的电场、磁场都应尽可能均匀,使所有电子的偏转程 度尽量相同.作为“临时偏转”,此电场或磁场会随时间变化,但变 化周期远大于电子渡越时间,故对电子运动可认为是“恒定”场: 环 行偏转线圈 场偏转线圈 12
12 ( ) dP F qe E v B dt = = +

用与处理轴对称场问题相似的方法,易得到偏转系统中电子 的运动轨迹方程: u,(Px')'=e ∂V ax 十By (av P=Pex+Pey+P.e:E=Eex+Eyey+E:e: v=v,ex+v,ey+v.e:B=Bex+Bey+B.e: 月 ex ey e: U:时xB= =(v,B.-v.B,)e.+(v.B,-v,B.)ey+(v,B,-v,B.)e- B.B B. 统P=gE+x,P=Px,B上 dt →y.(Py)'=e -v.B
13 ( ) ( ) ( ) ( ) , , x y z x y z x y z x y z x y z x y z x y z y z z y z x x z x y y x x y z x z y z x P P e P e P e E E e E e E e v v e v e v e B B e B e B e e e e v B v v v v B v B e v B v B e v B v B e B B B dP qe E v B P P x P P y dt dP qe E dt = + + = + + = + + = + + = = − + − + − = + = = = ( ) ( ) ( ) ( ) 1 1 , 1, , 0 1 1 , 1, , 0 z x z z y z V v q E B dt dz x x y z z y z z z y V v q E B y dt dz y y z x x z z z z x V v B v B v P x e v B x dP V qe E v B v B v P y e v B dt y = =− =− = = =− =− = + − ⎯⎯⎯⎯⎯⎯⎯⎯⎯→ = + = + − ⎯⎯⎯⎯⎯⎯⎯⎯⎯→ = −

u(Pxy'=ea那 v(Py)'=e av -V.B 方程的自变量是之,变量是x和y.因为是偏转系统,方程右边 应出现变量为0时并不等于0的“常数项”,它是之的函数.如果偏 转系统“好”,该项应该不随x或y变化,至少它对x和y的一阶 微商应该为0,故不改变高斯聚焦性能:且可在包括等于0的某一 范围内调变,故可使理想粒子呈正、负偏转或仍沿之轴前进.至于 静电偏转或磁偏转的分野,则显然在于右边分别只有方程中的第 一项或第二项.此外,对任一类偏转系统,两个方向应彼此无关,可 相互独立地调节. 14
14 ( ) ( ) z z z y z z z x V v P x e v B x V v P y e v B y = + = −

v.(Px)-e 方程左边的简化牵涉到旁轴条件.该条件成立意味着x2《 1,y<1因此u≈u和P≈卫.再加上偏转系统可认为位于 av -0的等位区(虽然Y或光可不为0).放P,和,不随:变化.应 该承认,这一假设用在此处颇感勉强.标志不理想程度的x'或y 一般是小量,而人为加上的偏转一此坐标系中也标为x'或y', 常常未必很小:偏转中P.的变化也许不可忽略.如果一丝不苟, 当偏转相当大时,必须用坐标系“跟着转”以保持旁轴条件的束流 传输理论处理(例如束流输运线):偏转较小而非很小时,仍可用上 述两个方程,但不忽略x2和y2项,将方程的解“分级”展开,先求 一级解即高斯轨迹,再逐级逼近.作为最简单的例子(如示波管 等),本节假设偏转角足够小,旁轴条件在偏转系统工作区仍成立
15 z z z y z z z x ( ) ( ) V V v P x e v B v P y e v B x y = + = −

v.(Px)'-e v.(PY)'=e -L.B P≈P 以u代表x或y:偏转力标为G.,其量纲是L1,单位多用 m1.方程可简化为 ”=G(z) 阴极出发的电子到V电势 能守:m- G= e∂V 对低能电子为2V分x 1av Pv ax 1 G,=B, 对低能电子为 2mV Py 2V 2e Gy=eov e m e Poay 对低能电子为2Vy 1av 2V 2V G=- B:对低能电子为 e 偏转系统的工作区取为之≤≤,工作长度L=红一之,工 作区以外设G(z)=0
16 z z z y z z z x ( ) ( ) V V v P x e v B v P y e v B x y = + = − P P z 2 V 1 1 2 2 1 2 2 2 2 2 eV mv vP e Pv V eV e v e m P V V mV = = = = = = 阴极出发的电子到 电势 能量守恒: