Capital per Year K K B ■■■■■ C, 1 L3 Labor per Year Producing a Given Output at Minimum Cost Copyright by Caidonghong
Copyright by Caidonghong Q1 A Labor per Year Capital per Year L3 L2 L1 C0 C1 C2 K2 K1 K3 Producing a Given Output at Minimum Cost B C

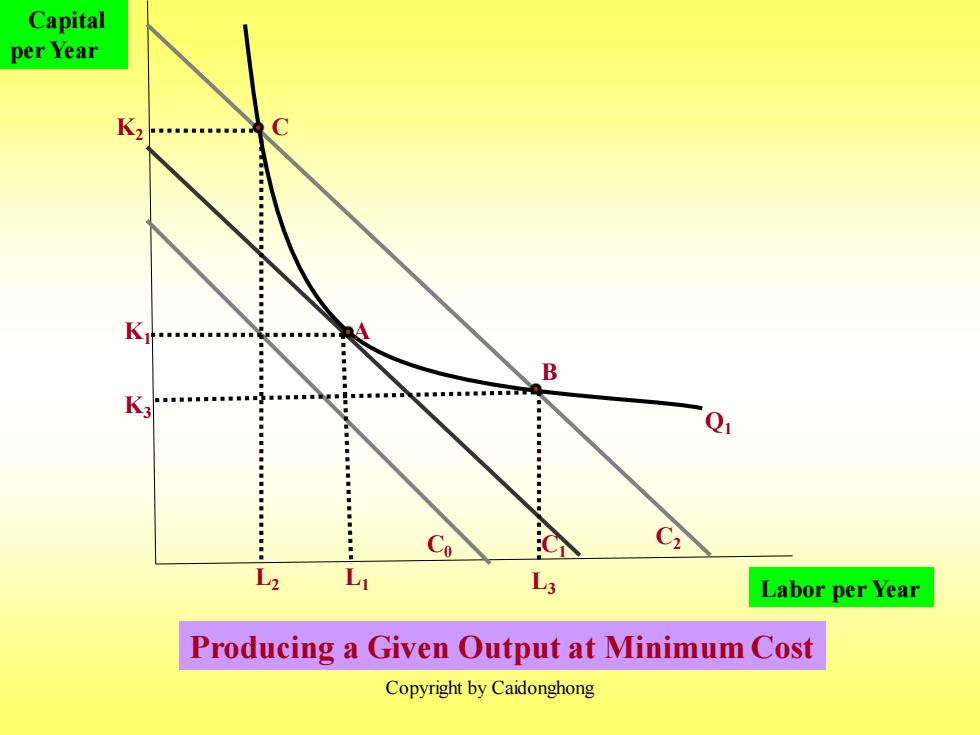
Isocost curves describe the combination of inputs to production that cost the same amount to the firm. Isocost curve C is tangent to isoquant Q at A and shows that output Q can be produced at minimum cost with labor input L and capital input K. Other input combinations-L2,K2 and L3,K3-yield the same output at higher cost. Copyright by Caidonghong
Copyright by Caidonghong Isocost curves describe the combination of inputs to production that cost the same amount to the firm. Isocost curve C1 is tangent to isoquant Q1 at A and shows that output Ql can be produced at minimum cost with labor input L1 and capital input Kl . Other input combinations-L2 , K2 and L3 , K3 -yield the same output at higher cost
Capital per Year B K Labor per Year Input Substitution when an Input Price Changes Copyright by Caidonghong
Copyright by Caidonghong Q1 A Labor per Year Capital per Year L2 L1 C2 C1 K1 K2 Input Substitution when an Input Price Changes B

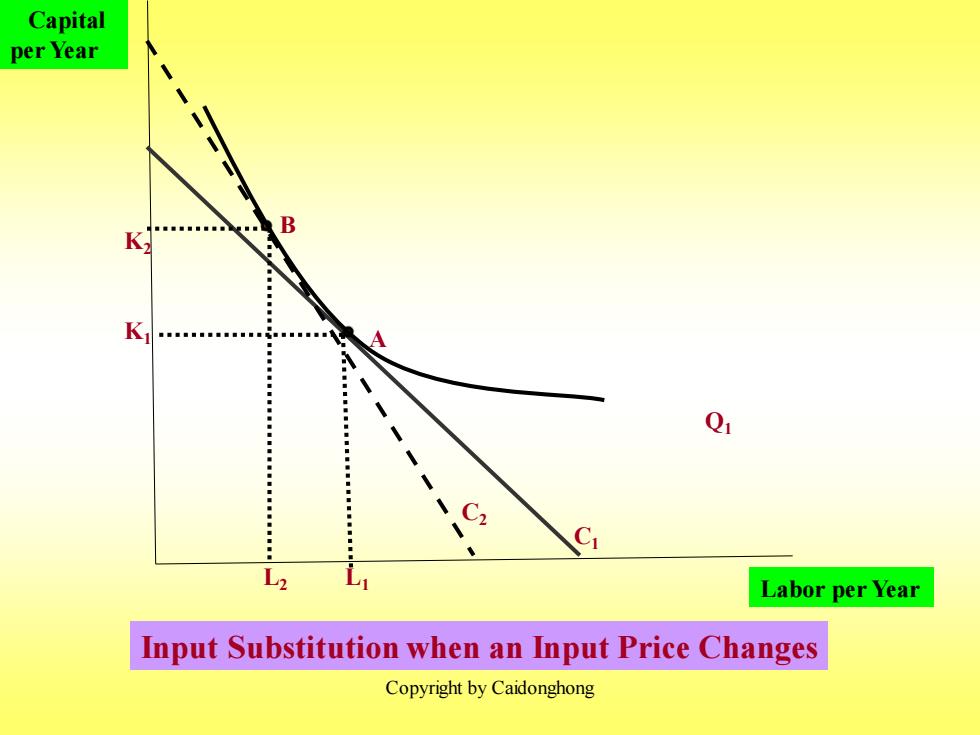
Facing an isocost curve Ci,the firm produces output Q at point A using L units of labor and K units of capital. When the price of labor increases,the isocost curves become Steeper.Output Q is now produced at point B on isocost curve C,by using L2 units of labor and K2 units of capital. Copyright by Caidonghong
Copyright by Caidonghong Facing an isocost curve C1 , the firm produces output Q1 at point A using L1 units of labor and K1 units of capital. When the price of labor increases, the isocost curves become Steeper. Output Q1 is now produced at point B on isocost curve C2 by using L2 units of labor and K2 units of capital

MRTS=-(△KW△L)=(MP)/MPK) We note that the isocost line has a slope of -△KW△L=(C/r)/(Cw)=wr. It follows that when a firm minimizes the cost of producing a particular output,.the following condition holds(适用): MP_/MPk-w/r We can rewrite this condition slightly as follows: MPL/w=MPk/r(7.4) Copyright by Caidonghong
Copyright by Caidonghong MRTS = - (△K/△L) = (MPL )/(MPK) We note that the isocost line has a slope of -△K/△L = (C/r)/(C/w)= w/r. It follows that when a firm minimizes the cost of producing a particular output, the following condition holds (适用) : MPL /MPK= w/r We can rewrite this condition slightly as follows: MPL/w = MPK/r (7.4)