
核外电子运动状态 4、跃迁规则 电子吸收光子就会跃迁到能量较高的激发态, 反过来,激发态的电子会放出光子,返回基态或能 量较低的激发态;光子的能量为跃迁前后两个能级 的能量之差,这就是跃迁规则,可以用下式来计算 任一能级的能量及从一个能级跃迁到另一个能级时 放出光子的能量: E= -2.179×1018 △E=2.179×1018 n
核外电子运动状态 4、跃迁规则 电子吸收光子就会跃迁到能量较高的激发态, 反过来,激发态的电子会放出光子,返回基态或能 量较低的激发态;光子的能量为跃迁前后两个能级 的能量之差,这就是跃迁规则,可以用下式来计算 任一能级的能量及从一个能级跃迁到另一个能级时 放出光子的能量: J 2179 10 2 1 8 n . E 2 2 2 1 1 8 1 1 2179 10 n n E

核外电子运动状态 由公式:△E=2.179×1018 及△E=E2-E=hv n 2.179×10-18 2.179×10-18 h 1n2 6.626×10-34 2 .V=3.289×1015 n n, 当n=1时能量最低, 此时能量为2.179×1018J,此 时对应的半径为52.9pm,称为玻尔半径。 能过理论计算得到的波长与实验值惊人的吻合, 误差小于千分之一。因此,玻尔理论曾风行一时
当n=1时能量最低,此时能量为2.179×10-18J,此 时对应的半径为52.9pm,称为玻尔半径。 能过理论计算得到的波长与实验值惊人的吻合, 误差小于千分之一。因此,玻尔理论曾风行一时。 核外电子运动状态 由公式: 2 2 2 1 1 8 1 1 2179 10 n n E . 及E=E2 -E1=h 2 2 2 1 1 8 2179 10 1 1 h n n . 2 2 2 1 3 4 1 8 1 1 6.626 10 2.179 10 n n 2 2 2 1 1 5 1 1 3.289 10 n n

核外电子运动状态 例:求激发态氢原子的电子从n=4能级跃迁到n=2 能级时所发射的辐射能的频率、波长及能量? 解:由 v=3.289×105 .y=6.167×1014s1 1=c=2.9979×108×10 -=486.1nm 6.167×1014 E=hy=6.6262×10-34×6.167×1014=4.086×1019(J)
核外电子运动状态 例:求激发态氢原子的电子从n=4能级跃迁到n=2 能级时所发射的辐射能的频率、波长及能量? 解:由 2 2 2 1 1 5 1 1 3.289 10 n n 2 2 1 5 4 1 2 1 3.289 10 1 4 1 6.167 10 s 486.1nm 6.167 10 c 2.9979 10 10 1 4 8 9 6.6262 10 6.167 10 4.086 10 (J) 3 4 1 4 -19 E h
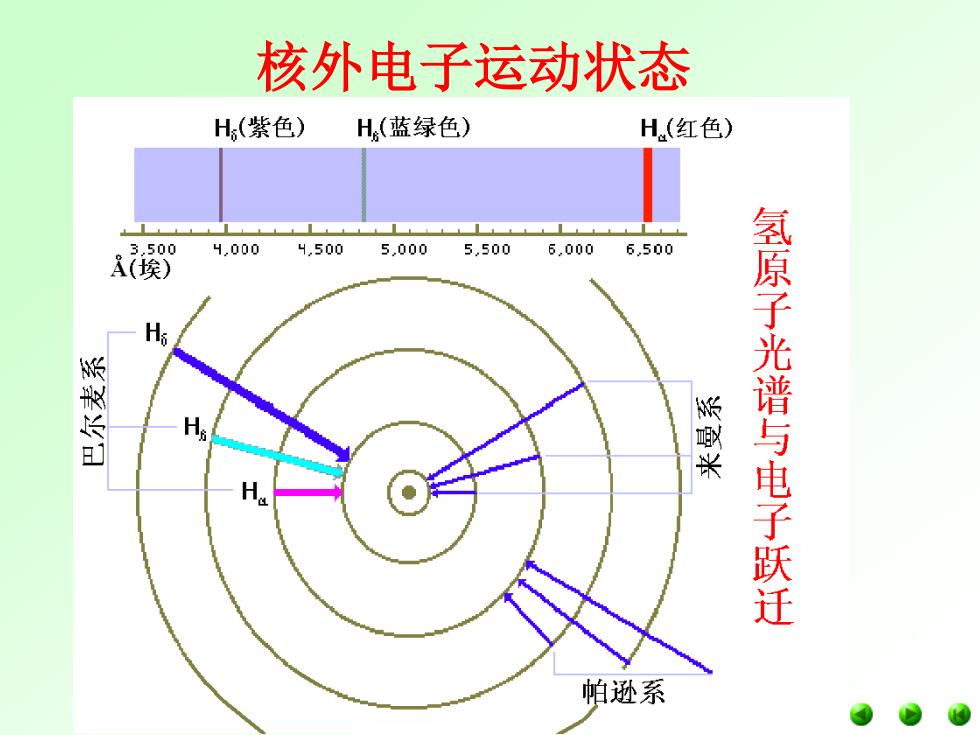
核外电子运动状态 H(紫色) H(蓝绿色) H(红色) 。。。。。 3500 4.000 4,5005,0005.500 6,0006.500 A(埃) 氢原子光谱与电子跃迁 帕逊系
核外电子运动状态

核外电子运动状态 行星轨道和行星模型是玻尔未彻底抛弃经典物 理学的必然结果,用玻尔的方法计算比氢原子稍复 杂的氦原子的光谱便有非常大的误差。 新量子力学证明了电子在核外的所谓“行星轨 道”是根本不存在的。玻尔理论合理的是:核外电 子处于定态时有确定的能量;原子光谱源自核外电 子的能量变化。这一真理为后来的量子力学所继承。 玻尔理论的基本科学思想方法是,承认原子体 系能够稳定而长期存在的客观事实,大胆地假定光 谱的来源是核外电子的能量变化,用类比的科学方 法,形成核外电子的行星模型,提出量子化条件和 跃迁规则等革命性的概念
核外电子运动状态 行星轨道和行星模型是玻尔未彻底抛弃经典物 理学的必然结果,用玻尔的方法计算比氢原子稍复 杂的氦原子的光谱便有非常大的误差。 新量子力学证明了电子在核外的所谓“行星轨 道”是根本不存在的。玻尔理论合理的是:核外电 子处于定态时有确定的能量;原子光谱源自核外电 子的能量变化。这一真理为后来的量子力学所继承。 玻尔理论的基本科学思想方法是,承认原子体 系能够稳定而长期存在的客观事实,大胆地假定光 谱的来源是核外电子的能量变化,用类比的科学方 法,形成核外电子的行星模型,提出量子化条件和 跃迁规则等革命性的概念