
二倍频峰:由v=0跃迁至v=2时,△v =2,产生的吸收峰称为~。 三倍频峰:由v=0跃迁至v=3时,△v =3,产生的吸收峰称为~。其它类推。 在倍频峰中,倍频峰的频率并不是基频峰 的整数倍而是稍小,二倍频峰还比较强。 三倍频峰以上,因跃迁几率很小,一般都 很弱,常常不能测到
二倍频峰:由υ =0跃迁至υ =2时, △ υ =2,产生的吸收峰称为~ 。 三倍频峰:由υ =0跃迁至υ =3时, △ υ =3,产生的吸收峰称为~ 。其它类推。 在倍频峰中,倍频峰的频率并不是基频峰 的整数倍而是稍小,二倍频峰还比较强。 三倍频峰以上,因跃迁几率很小,一般都 很弱,常常不能测到

3、分子中基团的基本振动形式 伸缩振动 弯曲振动(变形振动) 伸缩振动: 原子沿键轴方向伸缩,键长发生变化而键角不变 的振动称为~,用符号ν表示。它又可以分为对称伸缩 振动(Vs)和不对称伸缩振动(Vas)。对同一基团, 不对称伸缩振动的频率要稍高于对称伸缩振动 对称伸缩振动 不对称伸缩振动 0=2853cm-1 o=2926cm-1
3、分子中基团的基本振动形式 伸缩振动: 原子沿键轴方向伸缩,键长发生变化而键角不变 的振动称为~,用符号表示。它又可以分为对称伸缩 振动(s)和不对称伸缩振动( as)。对同一基团, 不对称伸缩振动的频率要稍高于对称伸缩振动 对称伸缩振动 不对称伸缩振动 σ=2853cm-1 σ=2926cm-1 弯曲振动(变形振动) 伸缩振动
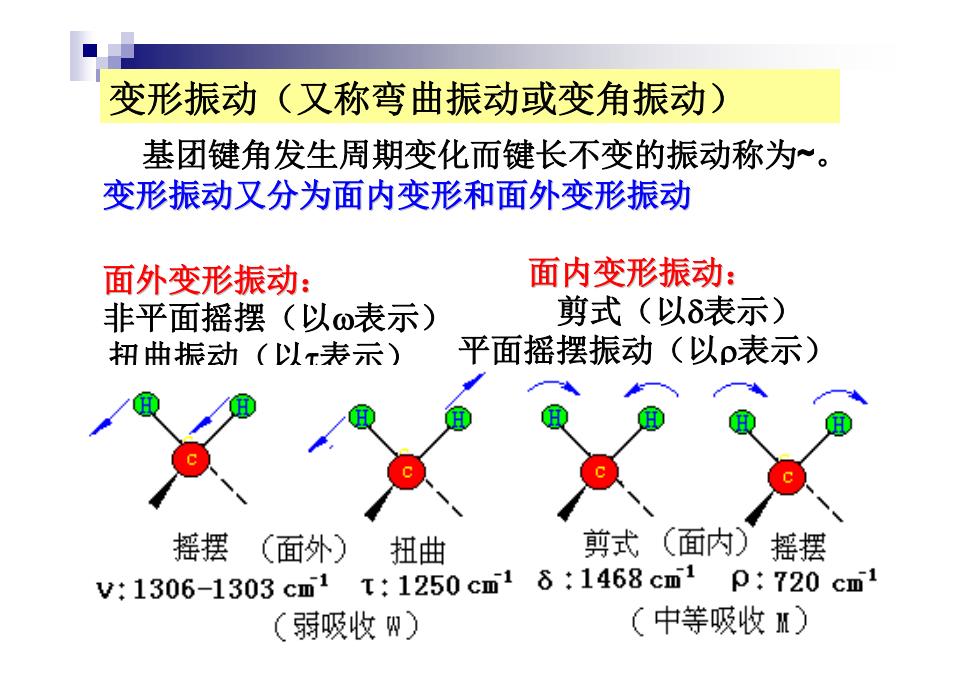
变形振动(又称弯曲振动或变角振动) 基团键角发生周期变化而键长不变的振动称为~。 变形振动又分为面内变形和面外变形振动 面外变形振动: 面内变形振动: 非平面摇摆(以ω表示) 剪式(以δ表示) 抑曲振动(以表示) 平面摇摆振动(以p表示) 摇摆 (面外)扭曲 剪式(面内)摇摆 V:1306-1303cm1T:1250cm1 6:1468cm1 p:720cm1 (弱吸收四) (中等吸收M)
变形振动(又称弯曲振动或变角振动) 基团键角发生周期变化而键长不变的振动称为~ 。 变形振动又分为面内变形和面外变形振动 面内变形振动: 剪式(以表示) 平面摇摆振动(以表示) 面外变形振动: 非平面摇摆(以表示) 扭曲振动(以表示)

4、基本振动的理论数(振动自由度) 多原子分子的振动数目称为振动自由度,每个振 动自由度相当于红外光谱图上一个基频吸收带。 设分子由n个原子组成,每个原子在空间都有3 个自由度,原子在空间的位置可以用直角坐标中的3 个坐标x、y、z表示,因此,n个原子组成的分子总 共应有3n个自由度,即3n种运动状态。但在这3n种 运动状态中,包括3个整个分子的质心沿x、y、z方 向平移运动和3个整个分子绕x、y、z轴的转动运动。 这6种运动都不是分子振动,因此,振动形式应有 (3n-6)种, 例如:水一非线型分子 振动自由度:3*3-6=3 有三种振动形式
4、基本振动的理论数(振动自由度) 多原子分子的振动数目称为振动自由度,每个振 动自由度相当于红外光谱图上一个基频吸收带。 设分子由n个原子组成,每个原子在空间都有3 个自由度,原子在空间的位置可以用直角坐标中的3 个坐标x、y、z表示,因此,n个原子组成的分子总 共应有3n个自由度,即3n种运动状态。但在这3n种 运动状态中,包括3个整个分子的质心沿x、y、z方 向平移运动和3个整个分子绕x、y、z轴的转动运动。 这6种运动都不是分子振动,因此,振动形式应有 (3n-6)种, 例如:水—非线型分子 振动自由度:3*3-6=3 有三种振动形式

直线型分子,若贯穿所有原子的轴是在x方向, 则整个分子只能绕y、z轴转动,因此,.直线性 分子的振动形式为(3n-5)种,二氧化碳一线 型分子 振动自由度:3*3-5=4有四种振动形式
直线型分子,若贯穿所有原子的轴是在x方向, 则整个分子只能绕y、z轴转动,因此,直线性 分子的振动形式为(3n-5)种,二氧化碳—线 型分子 振动自由度:3*3-5=4 有四种振动形式