分子的振动形式及振动光谱 1、以双原子分子振动光谱为例, 说明红外光谱 产生的条件 化学键的振动类似于连接两个小球的弹簧 虎克定律 1 U三 4二01m2 2π m1十m2 1=0 mA
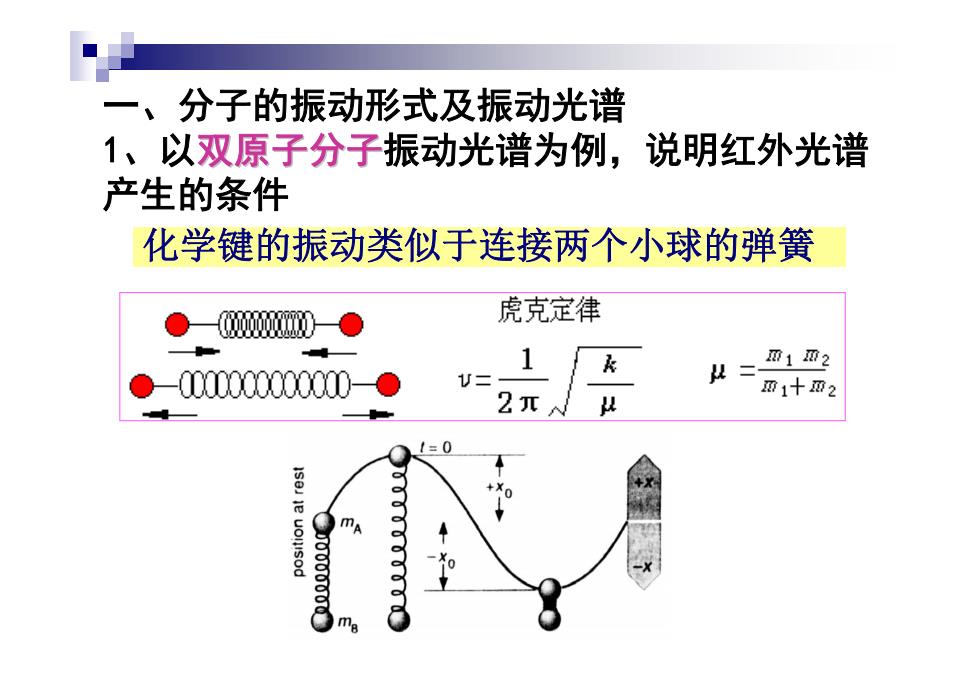
一、分子的振动形式及振动光谱 1、以双原子分子振动光谱为例,说明红外光谱 产生的条件 化学键的振动类似于连接两个小球的弹簧

分子的振动能级(量子化): E振=(v+1/2)hy y:化学键的振动频率; 0:振动量子数,可取0,1,2,3。 谐振子的跃迁选律为 △v=士1,△E=hco 只有当红外辐射频率等于振动量子数的差值与分 子振动频率的乘积时,分子才能吸收红外辐射, 产生红外吸收光谱
谐振子的跃迁选律为 △υ=±1, △E= hcσ 只有当红外辐射频率等于振动量子数的差值与分 子振动频率的乘积时,分子才能吸收红外辐射, 产生红外吸收光谱。 分子的振动能级(量子化): E振=(υ+1/2)h :化学键的 振动频率; υ :振动量子数,可取0,1,2,3

振动频率计算公式: k 2x u K K 1370 2πcV 可见分子的振动频率与化学键的力常数、原子质量有关
u k 2π 1 1370 2 1 c 可见分子的振动频率与化学键的力常数、原子质量有关。 振动频率计算公式:

折合质量 m m2 (m1+m2) 键的力常数k:其定义为将两个原子由平衡位置伸 长单位长度时的恢复力,单位N.cm1
(m m ) m m μ 1 2 1 2 折合质量 键的力常数k:其定义为将两个原子由平衡位置伸 长单位长度时的恢复力,单位N.cm-1

1)、折合质量越小,伸缩频率越高。 含氢官能团的伸缩振动能级跃迁发生在红 外光谱的高频区。 2)、折合质量相同的基团,伸缩力常数K越大, 伸缩振动基频峰的频率越高。 3)、折合质量相同时,通常伸缩振动〉面内摇 摆振动〉面外弯曲振动,因为他们的力常数 依次减小
1)、折合质量越小,伸缩频率越高。 含氢官能团的伸缩振动能级跃迁发生在红 外光谱的高频区。 2)、折合质量相同的基团,伸缩力常数K越大, 伸缩振动基频峰的频率越高。 3)、折合质量相同时,通常伸缩振动〉面内摇 摆振动〉面外弯曲振动,因为他们的力常数 依次减小