
§2.3力学量的算符 ·对波函数做某一数学运算,即用某一算符 作用于波函数,等效于用某一力学量乘以 波函数 -ih Ox =pxΨ -ihVw=p必 访 0Ψ =Ew Ot px =-ih p=-iV龙=访 Ox 8t [- V2+V(x)]w(x)=Ew(x) =X 21m E=- V(x)= (x)=V(x) 2m
§2.3 力学量的算符 • 对波函数做某一数学运算,即用某一算符 作用于波函数,等效于用某一力学量乘以 波函数 i E t i p x i p x ˆ x p i x p ˆ i E i ˆ t 2 2 [ ( )] ( ) ( ) 2 V E m x x x 2 2 ˆ ˆ ( ) 2 E V H m x x x ˆ ˆ V V ( ) ( ) x x
角动量算符 L=rxp i=r×(-hV) Z 在直角坐标系中 立=yp.-印,=-ih(y a 工,=印-p.=-(2 一X y &x ∂z i.=xp,-yp:=-ih(x ∂ 在球坐标系中 2-io品m0品+a] 2 D=一访
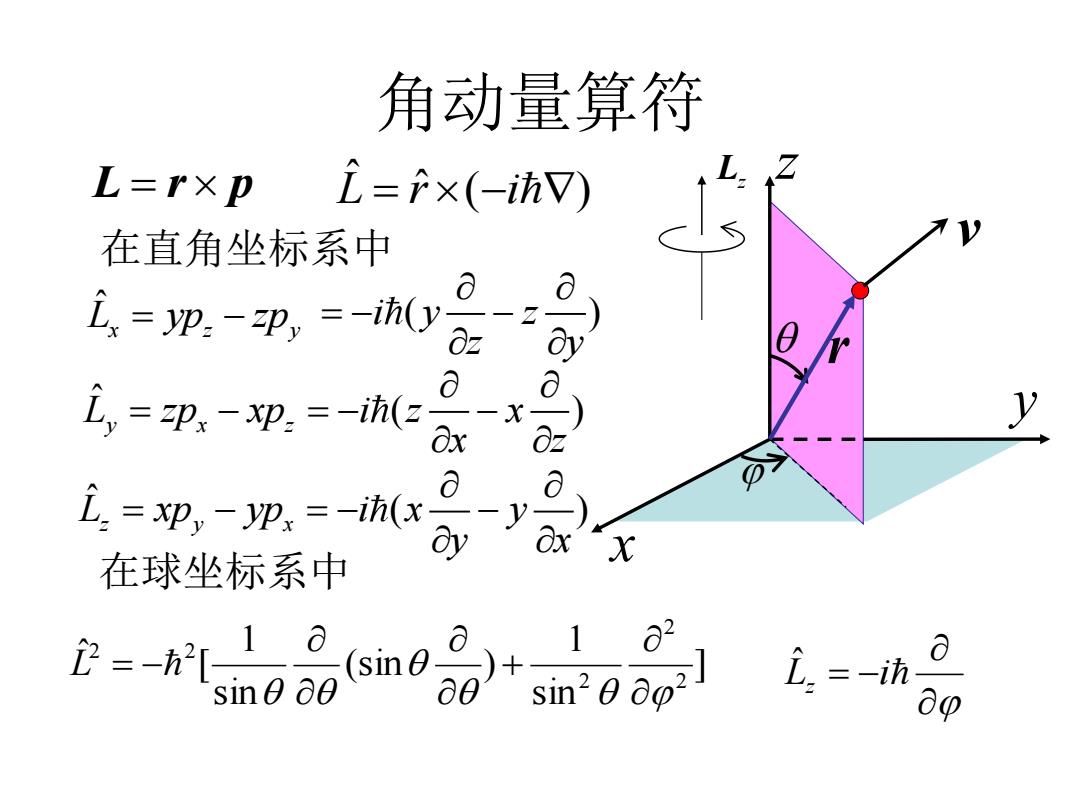
角动量算符 r v L z x y z L r p ˆ ( ) L ˆ r i ˆ L yp zp x z y ˆ ( ) L zp xp i z x y x z x z ˆ ( ) L xp yp i x y z y x y x Lz i ] ˆ sin 1 (sin ) sin 1 [ ˆ 2 2 2 2 2 L 在直角坐标系中 i y z ( ) z y 在球坐标系中

表象与力学量的平均值 x)为粒子的波函数,x)P表示粒子在x处出现 的几率,即粒子的位置值等于x的几率 则x的平均值为 xw(xdx=w(x)x(x)dx =w(x)xw(x)]dx =w(x)儿w(x)]dx 粒子的势能由其位置决定,其势能等于(x)的几 率为x)2,则x)的平均值为 F-∫V(x)川yw(x)Pdx=∫y(x)Vy(xdx =w(x)w(x)]dx
表象与力学量的平均值 • Ψ(x)为粒子的波函数,|Ψ(x)|2表示粒子在x处出现 的几率,即粒子的位置值等于x的几率 • 则x的平均值为 2 x x x x | ( ) | d ( )[ ( )]d x x x x ˆ • 粒子的势能由其位置决定,其势能等于V(x)的几 率为|Ψ(x)|2 ,则V(x)的平均值为 2 V V x x x ( ) | ( ) | d ( )[ ( )]d x V x x ( ) ( )d x x x x ( )[ ( )]d x x x x ˆ ( )[ ( )]d x V x x

。 但粒子的动量为p的几率,却不能直接用 x)描述 要计算动量p的平均值,必须知道关于p的 几率分布函数(p) ·p(p)为动量表象下的波函数,表示非单色波 中,波长值为=h/p的几率幅 ·实际就是波长为λ的单色成分的振幅 2π w(x)=∑a(2em ∑p(p)epn h
• 但粒子的动量为p的几率,却不能直接用 Ψ(x)描述 • 要计算动量p的平均值,必须知道关于p的 几率分布函数φ(p) • φ(p)为动量表象下的波函数,表示非单色波 中,波长值为λ=h/p的几率幅 • 实际就是波长为λ的单色成分的振幅 / ( ) ( )eik x x a 2 k h p / ( )eip x p

(x)为位置表象下的波函数,表示粒子(即 波包)在位置空间的几率幅(复振幅) ·波包x)为一系列振幅为p(p)的不同波长的单 色波叠加的结果 )ea∫pedp 其Fourier反变换即为动量的波函数 opD=2a肉=xedn
• Ψ(x)为位置表象下的波函数,表示粒子(即 波包)在位置空间的几率幅(复振幅) • 波包Ψ(x)为一系列振幅为φ(p)的不同波长的单 色波叠加的结果 / 3 3/ 2 1 ( ) ( )e d (2 ) i p x x p p / 3 3/ 2 1 ( ) ( )e d (2 ) i p x p x x 其Fourier反变换即为动量的波函数