《信号与系统》课程教学资源（PPT课件讲稿）第三章 周期信号的傅里叶级数表示

3.3连续时间周期信号的傅里叶数表示 例3.2傅里叶级数与周期信号(P132图34) x()= 之xe2,x-x3￥=00rh>3,=2r,7 2元 () 0=l+(e2+e2)+ +e 欧拉 常数项 二次谐波分量 方程 次谐波分量 三次谐波分量 x(1)=1+cos2mt+cos4xt+-cos6mt 3

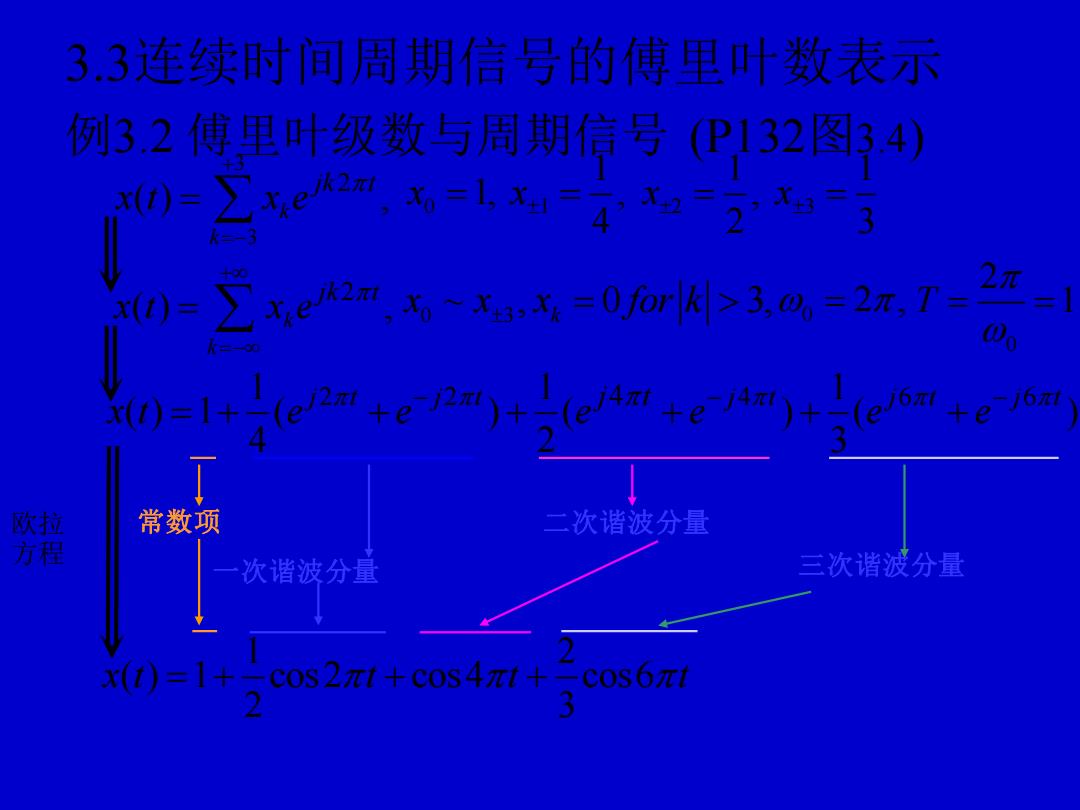
3.3连续时间周期信号的傅里叶数表示 例3.2 傅里叶级数与周期信号 (P132图3.4) 3 3 2 ( ) , k k jk t x t x e  + =− =  2 ( ) , k k jk t x t x e  + =− =  1 1 1 2 2 4 6 6 4 ( ) 1 ( ) ( ) ( ) 4 2 3 j t j t j t j t j t j t x t e e e e e e      − − −  = + + + + + + 1 2 ( ) 1 cos2 cos4 cos6 2 3 x t t t t = + + +    常数项 一次谐波分量 欧拉 方程 0 1 2 3 1 1 1 1, , , 4 2 3 x x x x = = = =    x x 0 3 ~ ,  0 3, k x for k =  0   = 2 , 0 2 T 1   = = 二次谐波分量 三次谐波分量

x(0)=I x(=c052T x()x(1) AAA A x,(t)=C0s47 x,)+x()+x( olatala x0=0s6 x(+x)+x(t)+( ◆

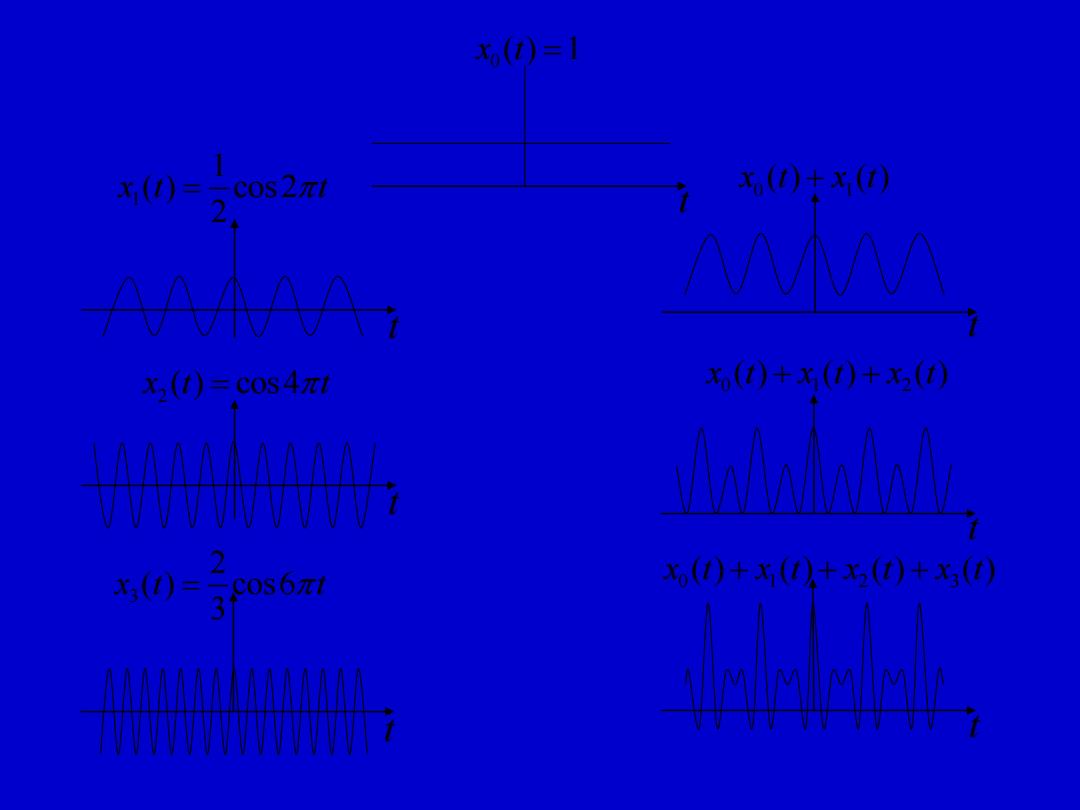
0 1 2 3 x t x t x t x t ( ) ( ) ( ) ( ) + + + 0 1 2 x t x t x t ( ) ( ) ( ) + + 0 1 x t x t ( ) ( ) + 3 2 ( ) cos6 3 x t t =  2 x t t ( ) cos4 =  1 1 ( ) cos2 2 x t t =  0 x t( ) 1 = t t t t t t t

例3.3复指数正弦信号的傅里叶级数的系数 (不用系数式 x(1)=S1no, 欧拉方程 x)= 号=00 <正弦函数的傅立叶级数展开，系数计算不用系数公式 直接将正弦函数展开成复指数的线性组合，直观确定系数

例3.3 复指数正弦信号的傅里叶级数的系数 0 x t t ( ) sin =  0 0 1 1 ( ) 2 2 j t j t x t e e j j   − = − 0 ( ) k k jk t x t x e  + =− =  1 1 ( , 2 x j  =  <正弦函数的傅立叶级数展开，系数计算不用系数公式, 直接将正弦函数展开成复指数的线性组合，直观确定系数> 欧拉方程 (不用系数公式) 0 1) k x for k =  

例3.5一般周期信号的傅里叶级数的系数 用系数公式 x() 2π w0= 如图3.6P136 T -T1T1 T x)=∑xea =7e'i=eav 1 2sin(koT)sin(ko T) 2)k0 7 k元

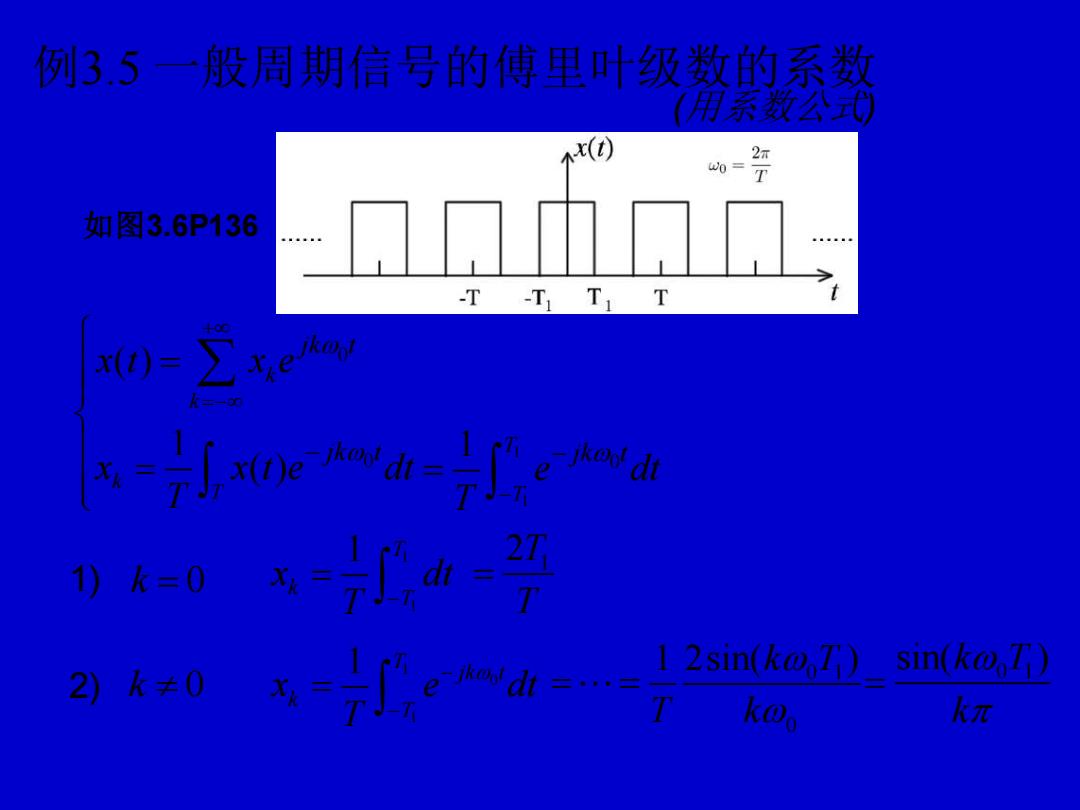
例3.5 一般周期信号的傅里叶级数的系数 如图3.6P136 0 0 ( ) 1 ( ) k k k T jk t jk t x t x e x x t e dt T   + =− −  =     =    1) k = 0 1 1 1 T k T x dt T − =  2) k  0 1 0 1 1 T jk t k T x e dt T −  − =  (用系数公式) 1 1 0 1 T T jk t e dt T  − − =  1 2T T = 0 1 0 1 2sin( ) k T T k   = = 0 1 sin( ) k T k   =

例3.8 x(1 0,=27/7 117 -27-T01727 0 2x/7 x0=∑6t-T X=1 的傅里叶级数 (d= w-立-们2。八呼

例3.8 x t( ) −2T −T 0 T 2T t 0   = 2 /T ( ) ( ) k x t t kT  + =− = −  0 / 2 / 2 1 ( ) T k T jk t x t e dt T   − − =  2 1 ( ) ( ) k k jk t T x t t kT e T   + + =− =− = − =   1 k x = 2 ( ) k k jk t T e T t kT   + + =− =−    = − 的傅里叶级数 F s k x 0  1/T 2 /  T 1 T =