
U K d2w M(x) dx2 p(x) EI p(x) w M(x) 3/2 EI dx 这就是挠曲线的微分方程。 12
12 , ( ) ( ) 1 EI M x x = = ( ) 1 x 3 / 2 2 2 2 dd 1 dd + xwxw 3 / 2 2 2 2 dd 1 dd + xwxw EI M (x ) = 这就是挠曲线的微分方程

dx M(x) 73/2 EI 1+ dx 挠曲线的近似微分方程 在小变形的情况下, dw d2w <<1 M(x) dx d x EI 方程中正负号的确定 13
13 挠曲线的近似微分方程 3/2 2 2 2 d d 1 d d + x w x w EI M (x) = 在小变形的情况下, 1 d d x w 2 2 d d x w EI M (x) = 方程中正负号的确定
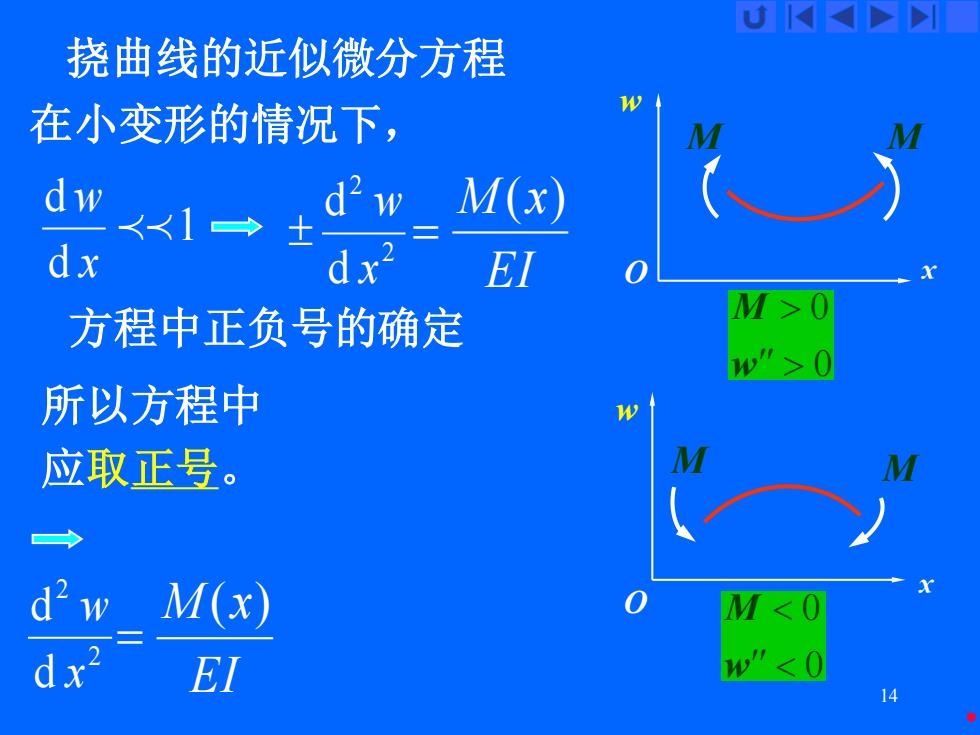
U K 挠曲线的近似微分方程 在小变形的情况下, dw d2w <<1→± M(x) dx dx2 EI 方程中正负号的确定 M>0 w">0 所以方程中 应取正号。 d2w M(x) dx2 EI 14
14 挠曲线的近似微分方程 在小变形的情况下, 1 d d x w 2 2 d d x w EI M (x) = 方程中正负号的确定 所以方程中 应取正号。 EI M (x) = 2 2 d d x w O x w x O w 0 0 M w 0 0 M w M M M M
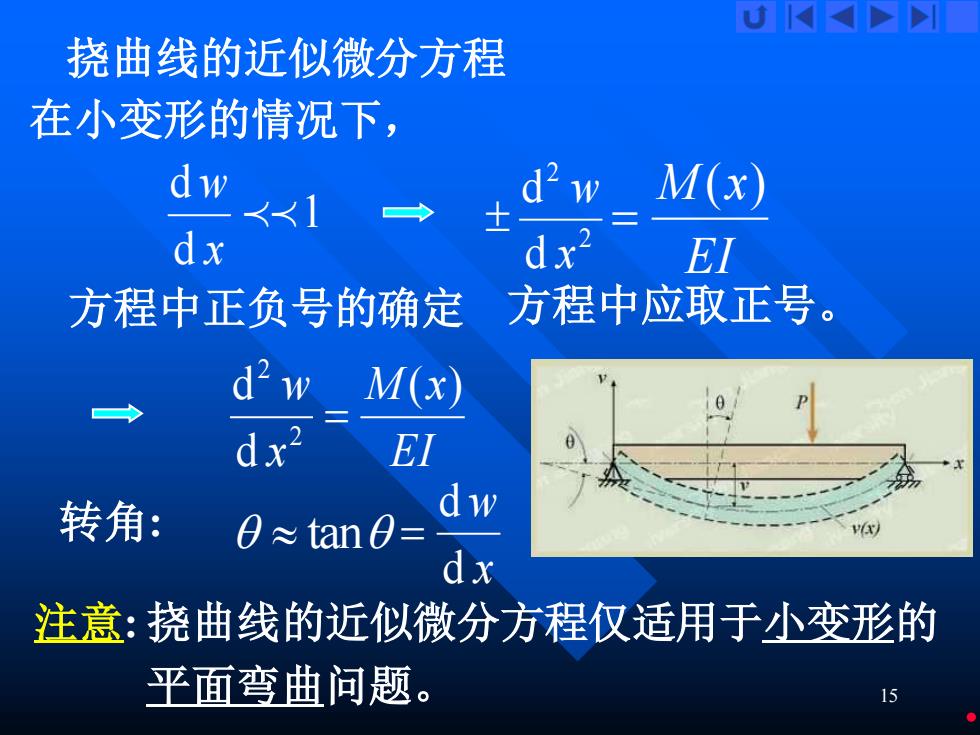
U K 挠曲线的近似微分方程 在小变形的情况下, dw d2w <<1 M(x) dx dx2 El 方程中正负号的确定 方程中应取正号。 d2w M(x) dx2 EI 转角: dw 0≈tan0= dx 注意:挠曲线的近似微分方程仅适用于小变形的 平面弯曲问题
15 挠曲线的近似微分方程 在小变形的情况下, 1 d d x w 2 2 d d x w EI M (x) = 方程中正负号的确定 方程中应取正号。 EI M x x w ( ) d d 2 2 = 转角: tan 注意: 挠曲线的近似微分方程仅适用于小变形的 平面弯曲问题。 x w d d =

注意事项一适用条件 0 1.应采用右手坐标系; 0 2.忽略剪力Q的影响; 3.小变形,w<1,或w≈0; 4.材料服从虎克定律。 16
16 注意事项—— 适用条件 1. 应采用右手坐标系; 2. 忽略剪力Q 的影响; 3. 小变形,w′<< 1, 或 w′≈ 0; 4. 材料服从虎克定律