
U K §6.3用积分法求弯曲变形 挠曲线近似微分方程 M(x) dx2 EI 积分一次,得 0= d w dx 再积分次川②6D 其中,C、D为积分常数,由边界条件确定。 边界条件
17 §6. 3 用积分法求弯曲变形 挠曲线近似微分方程 积分一次,得 EI M x x w ( ) d d 2 2 = x w d d = 再积分一次,得 x x Cx D EI M x w + + = d d ( ) 其中,C、D为积分常数 边界条件 x C EI M x = + d ( ) ,由边界条件确定
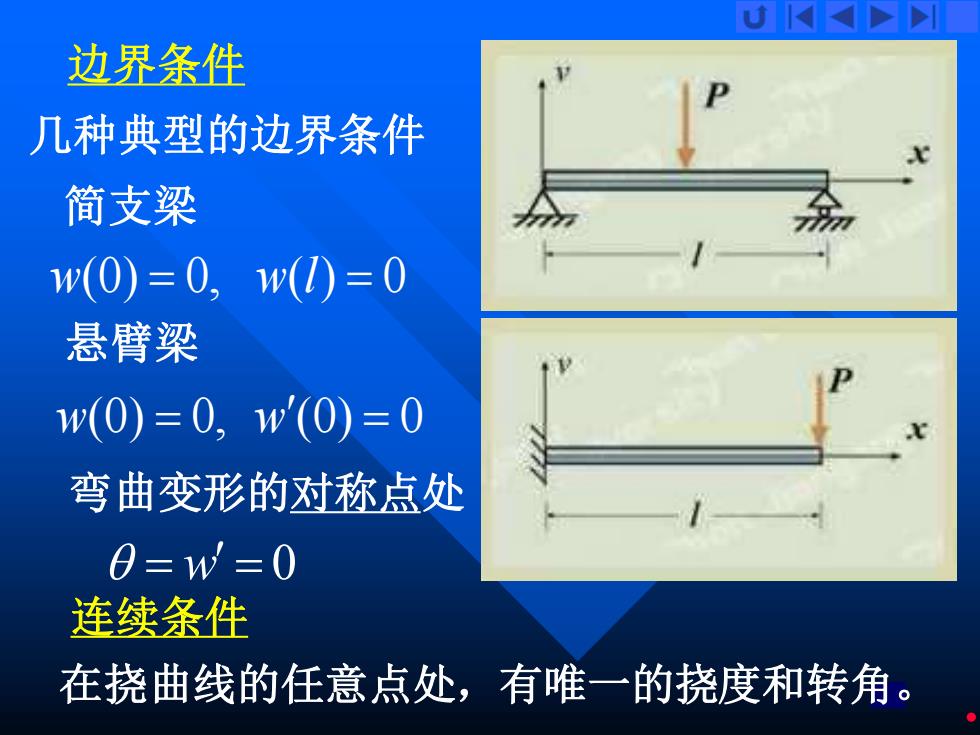
边界条件 几种典型的边界条件 简支梁 w(0)=0,w()=0 悬臂梁 w(0)=0,1'(0)=0 弯曲变形的对称点处 0=1wW=0 连续条件 在挠曲线的任意点处,有唯一的挠度和转角
18 边界条件 几种典型的边界条件 简支梁 悬臂梁 w(0) = 0, w(l) = 0 w(0) = 0, w (0) = 0 连续条件 弯曲变形的对称点处 = w = 0 在挠曲线的任意点处,有唯一的挠度和转角
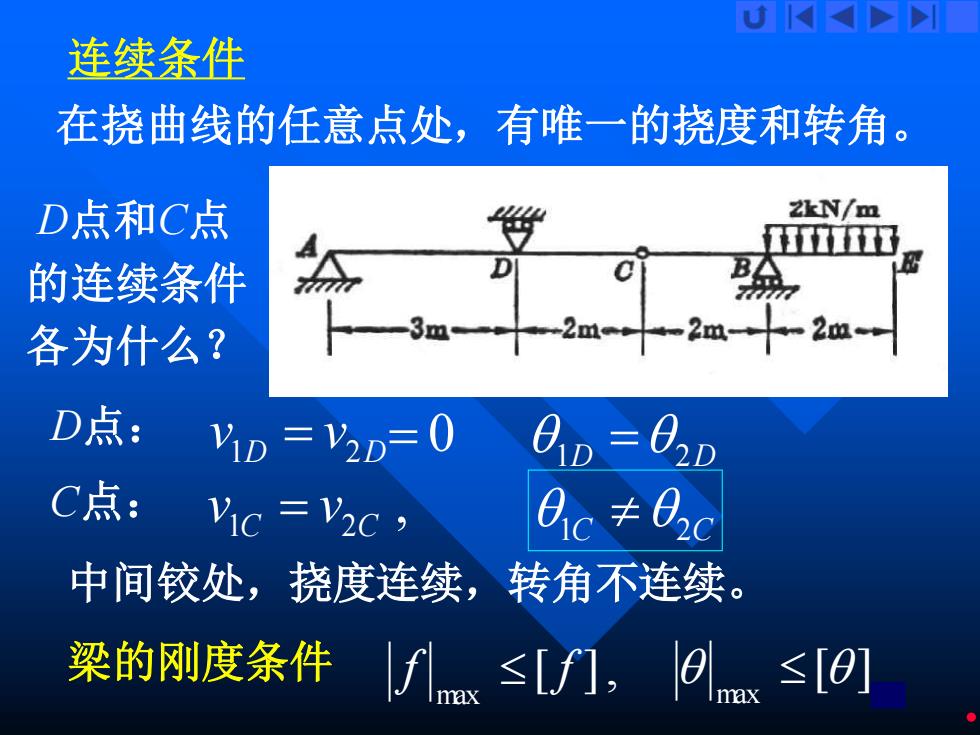
UK>> 连续条件 在挠曲线的任意点处,有唯一的挠度和转角。 D点和C点 ZkN/m 的连续条件 各为什么? -3m一-2m2m-2m D点: YD =V2D=0 0D=02D C点: Vic =V2c 0c≠0c 中间铰处,挠度连续,转角不连续。 梁的刚度条件 f≤[f,s≤[e]
19 梁的刚度条件 [ ], max f f [ ] max 连续条件 在挠曲线的任意点处,有唯一的挠度和转角。 D D v v 1 = 2 D点和C点 的连续条件 各为什么? D点: C点: 1D = 2D , 1C 2C v = v 1C 2C 中间铰处,挠度连续,转角不连续。 = 0
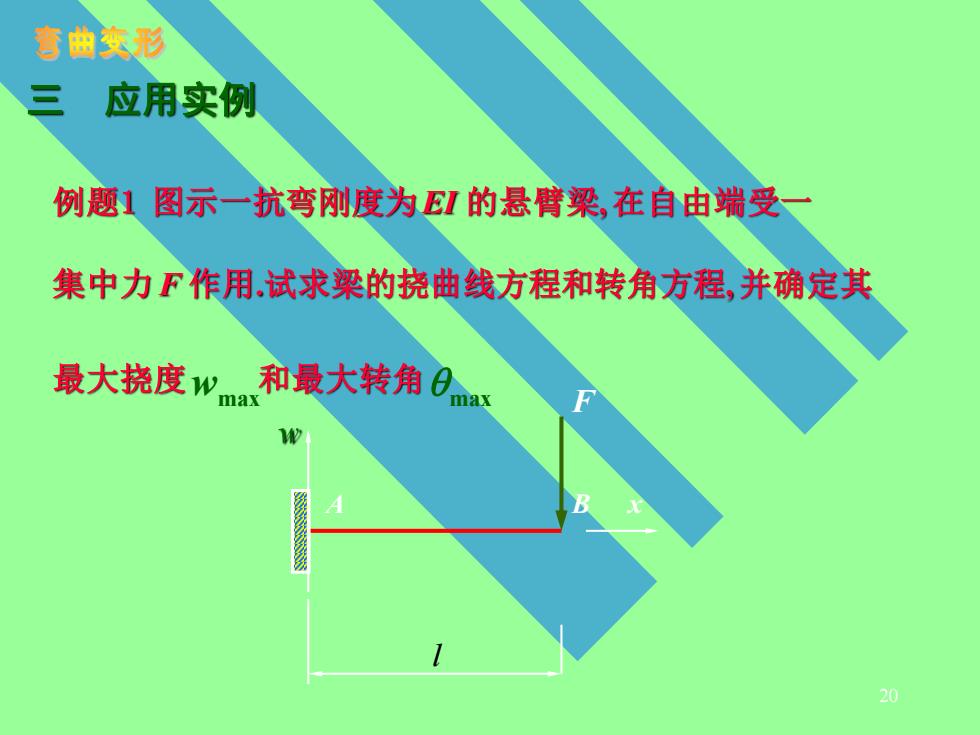
弯曲变形 三 应用实例 例题1图示一抗弯刚度为EI的悬臂梁,在自由端受一 集中力F作用试求梁的挠曲线方程和转角方程,并确定其 最大挠度w和最大转角0y
20 例题1 图示一抗弯刚度为EI 的悬臂梁, 在自由端受一 集中力 F 作用.试求梁的挠曲线方程和转角方程, 并确定其 最大挠度 和最大转角 l A B x F w wmax max 三 应用实例