
XINHUANET
7

www.wpeu.cn
8
U K §6.2挠曲线的微分方程 1基本概念 挠曲线 梁的轴线变形后的曲线。 对称弯曲时,是一条平面曲线。 弯曲变 形的度量 挠度 横截面形 心沿y方向 的位移,用w表示
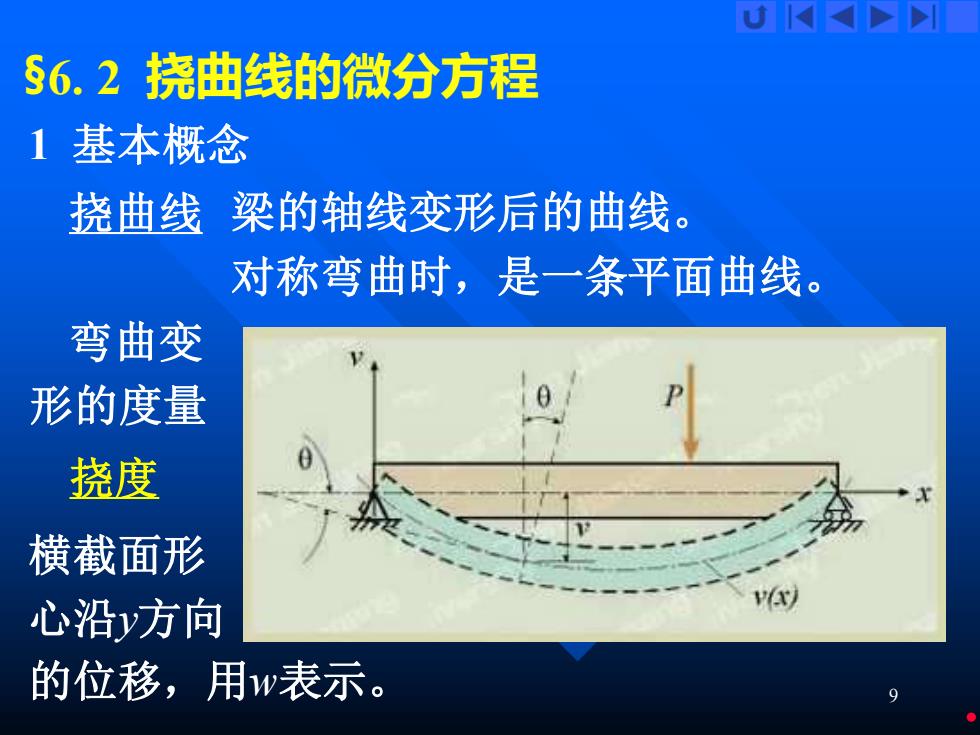
9 §6. 2 挠曲线的微分方程 1 基本概念 梁的轴线变形后的曲线。 对称弯曲时,是一条平面曲线。 弯曲变 形的度量 挠度 横截面形 心沿y方向 的位移,用w表示。 挠曲线
U 挠度 横截面形心沿y方向 的位移,用表示。 转角 变形后,横截面相对其原来位置转过的角度。 用0表示。转角0以逆时针为正。 挠曲线方程 w=f(x) 转角即为挠曲线在该点的切线与x轴的夹角。 dw tan 0 dx 10
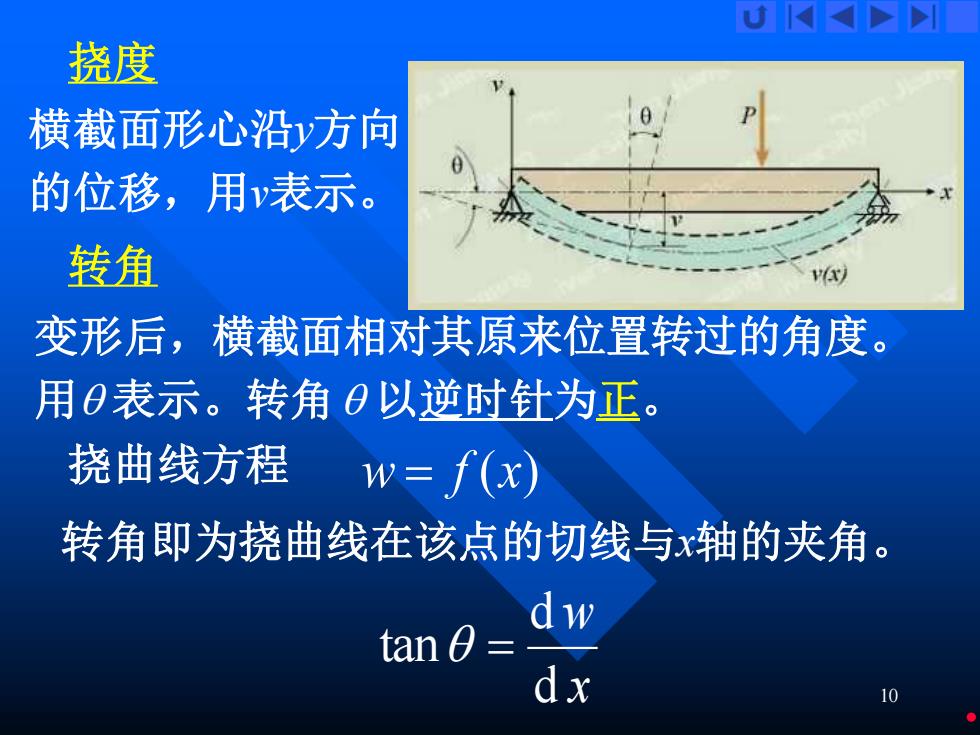
10 挠度 横截面形心沿y方向 的位移,用v表示。 转角 变形后,横截面相对其原来位置转过的角度。 用 表示。转角 以逆时针为正。 挠曲线方程 w = f (x) 转角即为挠曲线在该点的切线与x轴的夹角。 x w d d tan =
2挠曲线的微分方程 上一章中,已得到:忽略剪力对变形的影响时, 梁对称弯曲时的曲率为 M(x) P(x) EI 由高等数学公式 M(x) d2w dx2 13/2 P(x) 1A) 1+ dx
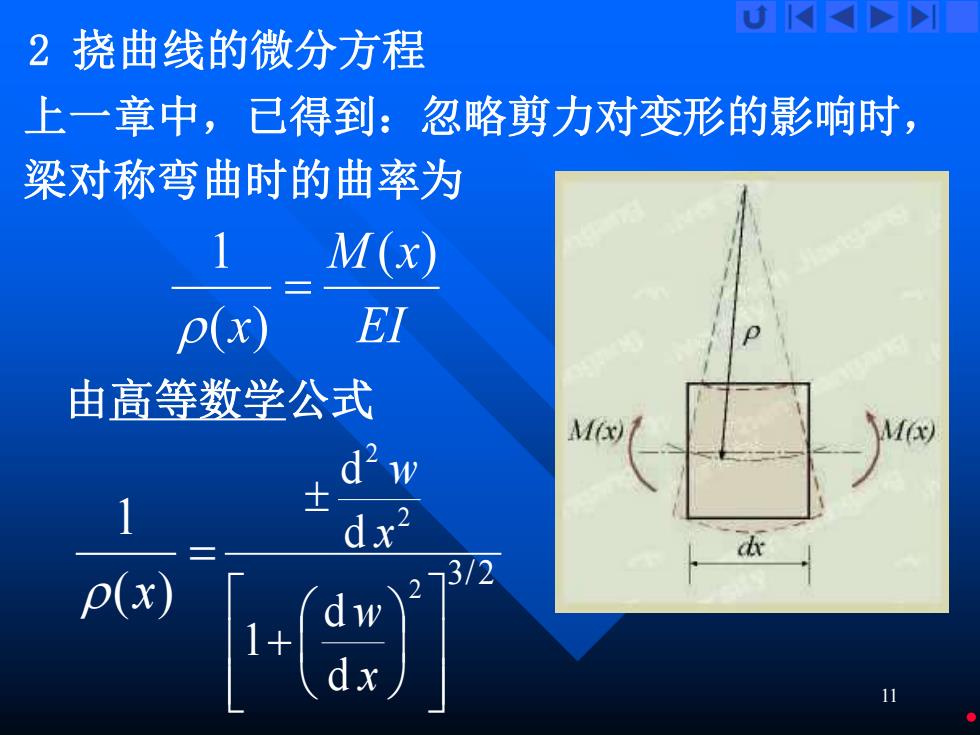
11 2 挠曲线的微分方程 上一章中,已得到:忽略剪力对变形的影响时, 梁对称弯曲时的曲率为 由高等数学公式 EI M x x ( ) ( ) 1 = = ( ) 1 x 3/2 2 2 2 d d 1 d d + x w x w