
24 第1章流体的流动及输送 剪力称做剪应力 推力 设有间距甚小的两平行板,其间充满流体,下版 固定,给上板施加一平行于平板的外力F,使平板以 速度“做匀速运动。紧贴在运动板上的流体以同 一速度“流动,而紧贴固定板的流体层则静止不 动,两板间各层流体的速度不同其大小如图119中 图119平板间液体速度变化图 的箭头所示。 实验证明,对大多数流体,剪应力:服从下述牛顿粘性定律: (1-45) 式中:r一剪应力,Nm2;du/dy一法向速度梯度,s'一比例系数,称为粘性系数或动力 度,简称粘度,单位为Nsm2或Pas。 牛顿粘性定律指出,流体的剪应力与法向速度梯度成正比,而与法向压力无关。流体的这 规律与固体表面的摩擦力的变化规律截然不同。 (二)流体的粘度 由牛顿粘性定律知 #=du/dy 粘度的物理意义是促使流体产生单位速度梯度的剪应力。粘度是流体的一种物性。通常 粘度只与温度有关,而与速度梯度无关。一般液体粘度随温度升高而减小,气体的粘度随温度 升高而增大。流体的粘度是影响流体流动的一个重要物理性质,许多流体的粘度可从有关手 册中查到,以往手册中粘度的单位为P(泊)或cP(厘泊),它们与SI单位制的Pas关系如下: 1cP=0.01P=102dyn·s/cm2=10-3Pa*s 实验证明,气体及水、溶剂、甘油等液体服从牛顿粘性定律,此类流体统称牛顿型流体。也 有不少流体不服从牛顿粘性定律,它们统称非牛顿型流体,如泥浆等。 1.4.2两种流动型态和雷诺准数 (一)雷诺实验证实两种流型 为了有接观察流体流动时内部质点的运动状况和各种因素的影响,1883年雷诺做实验进行 了研究。图120即雷诺实验装置示意图。在一个透明水箱内,水箱下方安装一个带喇叭形进口 的玻璃管,管下游装有阀门,用阀门调节管内流 址。在管中心处有一根针形小管,自小管流出 丝有色水流,其密度与水几乎相同。 当水的流量较小时,玻管水流中出现一 丝稳定而明显的有色直线。随着流速增加 日E 起初流线保持平滑直线,当流速增至某临界 值后,有色线条开始抖动、弯曲,最后完全与 水流主体混合 图120诺实验 实验现象揭示了流动的机理,流体流动存 在着两种截然不同的流型,一种是流体质点作直线运动,即流体分层流动,层次分明,致使有色流

1.4流体的流动现象 25 线稳定平滑,这种流型称作层流或滞流。另一种是流体质点总体上沿管道向前流动,同时质点也 向各个方向做随机运动,彼此混合,致使其中的有色流线被搅混,这种流型称作湍流或紊流。 (二)流型的判据—雷诺数 雷诺实验表明,流体流型不仅与流速u有关,还与流体的密度、粘度和流道的几何尺 寸1(若为圆管则1为管内径d)有关。雷诺发现,将这些影响因素组成一个数群,可作为流型 的判据。这一数群称为雷诺准数简称雷诺数,以Re表示。 Re=dug (1-46) R准数是一个无量纲数群,无论采用何种单位制,只要数群中各物理量的单位一致,算出 的Re数必定是.个相等的纯数。 雷诺指出: (1)当Re<2000时,流动总是层流状态,称为层流区; (2)当2000<Re<4000时,有时出现层流,有时出现湍流,与外界条件有关,称为过渡区: (3)当R>4000时.,流动呈现常流型态,称为湍流区。 这里以R数为判据,将流动分为层流区、过渡区和湍流区,但流型只有两种层流和湍流, 过渡区的流动实际上处于不稳定状态,究竞出现何种流型,需视外界扰动而定。 R数之所以可用做流型的判据,是因为它反映了惯性力与粘性力之比 惯性力ocpu2 粘性力∝μ 款=片==Re 当惯性力大时,Re数大,湍动程度强;当粘性力大时,Re数小,将抑制流体的湍动 1.4.3层流和湍流的特征 (一)两种流型流体质点运动的特征 流体在管内作层流流动时,其质点沿管轴作有规则的一维运动,各质点互不碰撞,互不混合 管内湍流时,流体质点的运动是杂乱无章的, 湍流被视为在流体平均前进运动之外,附加有无 数漩涡的不规则高频脉动。对这种运动,人们采 用了统计方法。就流速而言,将湍流中任何一个 质点的速度向量分解为两部分,一个是时均速度 分量,它不随时间而变,另一个是脉动速度分量 它在时均速度上下波动。在直角坐标系中,令流 体质点在x、y、:三个方向上的瞬时速度分别为 “,4,时均速度分别为4、,、,脉动速度分 图121湍流中瞬时、时均与 别为、山,、u,则其关系如下 脉动速度之间的关系困 uy=uy us (1.47) u:=认:+u:

26 第】章流体的流动及输送 就x方向,任一流体质点在0一t时间范围内的时均速度4,(如图121所示)为 w.=Ifoudt (1.48) 式中“为该流体质点的瞬时速度,是时间的函数:当取得足够长时,时均速度,在内 是一个常数。由于脉动速度的频率很高,实际上t只需几秒。 从微观上讲,湍流根本无所谓定态,但就统计的观点,湍流又是定态。这是指时均址而言 即如果时均量在所选的时间内具有恒定量,这样的湍流可以认为是定态湍流。 所谓脉动址是指距时均量的偏离量,就脉动速度,它相对于时均速度,有时为正有时为负, 因此脉动速度4,在0一t范围内的时均量址,必为零。那么在径向上,双,=0,立。=0,瞬时速 度t,=u,.=w,正是径向脉动速度加强了动量、能量和质量的传递。 (二)流体在圆管内流动的速度分布 因为流体具有粘性,无论是层流或湍流,在管道的任一截面上,流体质点的速度都沿管径而 变。管坠处为零,离开管壁速度渐增,至中心处速度最大。速度在管裁面上的分布,因流型而异, 层流时,流体层间的剪应力服从牛顿粘性定律,由此可用数学分析法推导层流速度分布表 达式。 在水平圆管中心处取一半径为r、长为d!的流体微元柱,作微元柱的受力分析,则 柱后端面受压力 P1=pr2 柱前端面受压力 P,=-(b+db)元r 柱侧面受剪力 F=-t(2xrdl) 流体做定态匀速运动,合力为零,则 p2-(p+dp)xr2-(2xrdl)=0 整理,得 0-2r=0 由式(1-45) r=-udu 联立上二式,得 r 按下列边值条件积分之,有 r=R,u=0;r=r,u=u odu ddr 得 (1-49) r=0处的速度最大,以“m表示,则 mr (1-50) 式(149)可写成 u=“1-司 (1-51) 式(1-51)即为圆管内层流的速度分布表达式。显然,u随,变化的函数曲线为抛物线,见图 1-22(a
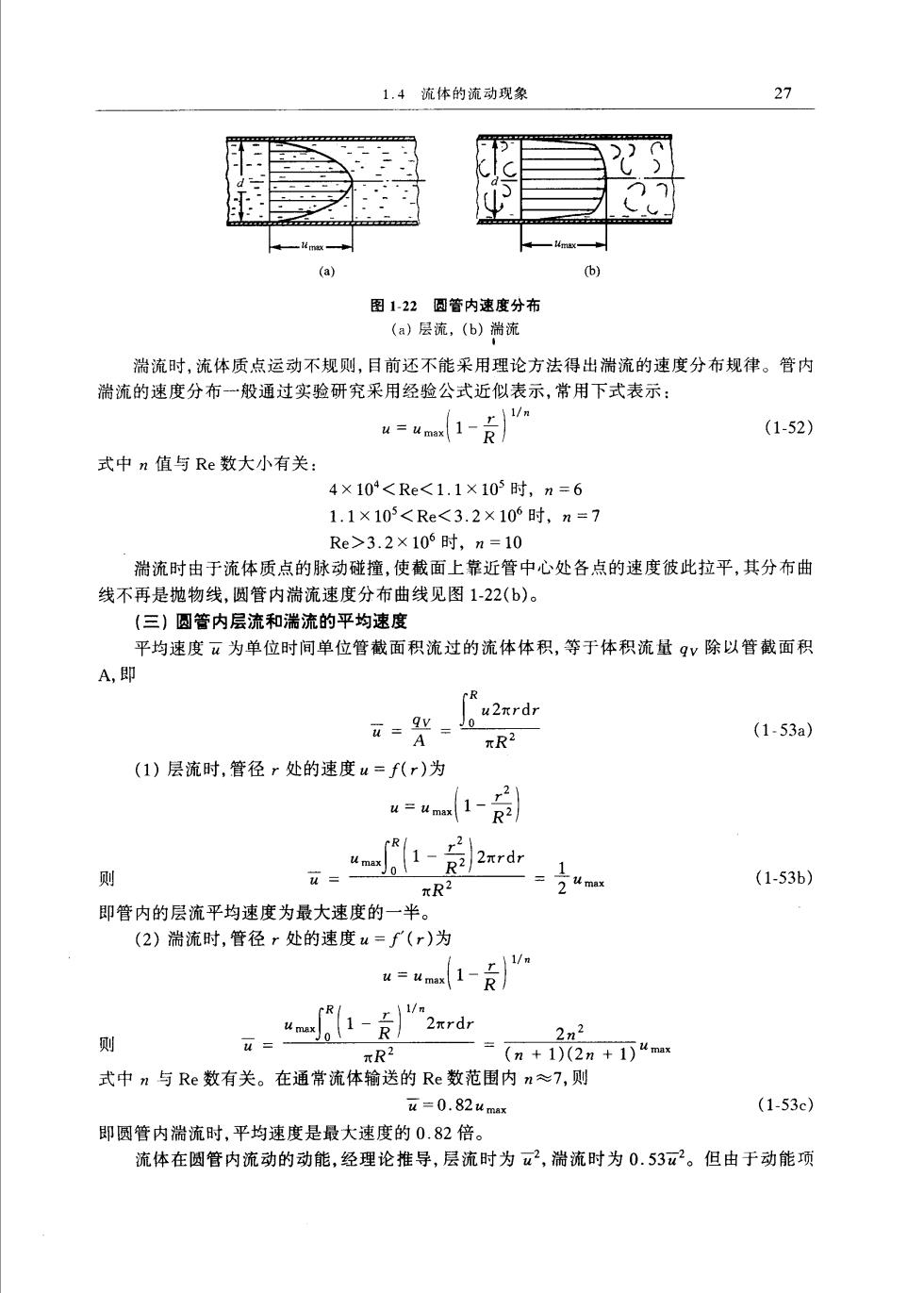
1.4流体的流动现象 27 图1-22圆管内速度分布 ()层流,(b)湍流 湍流时,流体质点运动不规则,目前还不能采用理论方法得出湍流的速度分布规律。管内 湍流的速度分布 一般通过实验研究采用经验公式近似表示,常用下式表示: (1-52) 式中n值与Re数大小有关: 4×10<Re<1.1×10时,n=6 1.1×103<Re<3.2×106时,n=7 Re>3.2×105时,n=10 湍流时由于流体质点的脉动碰撞,使截面上靠近管中心处各点的速度彼此拉平,其分布曲 线不再是抛物线,圆管内湍流速度分布曲线见图1-22(b)。 (三)圆管内层流和湍流的平均速度 平均速度“为单位时间单位管截面积流过的流体体积,等于体积流量gv除以管截面积 A,即 R2 (1-53a) (1)层流时,管径r处的速度u=f(r)为 =a1-动 多 =1-动2dr」 W- xR2 (1-53b) 即管内的层流平均速度为最大速度的一半。 (2)湍流时,管径r处的速度u=∫(r)为 1- 则 2n2 πR2 :=(n+1)(2n+1万4m 式中?与Re数有关。在通常流体输送的Re数范围内n≈7,则 a=0.824m (1-53c) 即圆管内湍流时,平均速度是最大速度的0.82倍。 流体在圆管内流动的动能,经理论推导,层流时为2,湍流时为0.532。但由于动能项

28 第1章流体的流动及输送 往往在各项能量的总和中所占的分数很小,故流体流动系统的动能,一般可取平均速度计算为 2/2,对于层流或湍流产生的误差一般均可忽略。请注意,仅在讨论速度分布时“代表点速 度,一般公式中u指平均速度。 1.4.4流体流动中的剪应力和动量传递 (一】层流状态的剪应力 粘性流体层流时的内摩擦阻力即剪应力服从牛顿粘性定律,即 层流剪应力从宏观上看是流体质点分层流动,速度较快的流体层给较慢的流体层一个推 力,较慢层则给较快层一个阻力,此推力和阻力为一对作用力和反作用力。它的物理本质是分 子热运动的吸引,碰撞和扩散的结果,较快层流体的分子扩散进入较慢层,使较慢层速度加快。 较慢层的分子扩散进入较快层,使较快层速度变慢,从而形成了法向上的速度梯度。 (二)满流状态的剪应力 湍流时,流体质点的不规则运动,产生了许多的漩涡,已不再有质点的分层运动,因此不能 用牛顿粘性定律描述。若仍沿用牛顿粘性定律的形式,则写成 r=-(+e0 (1-54) 式中:为涡流粘度,它与流体的物性无关,而与湍动强度、管壁粗糙度等因素有关。很难确 定,且4,所以湍流主体的速度分布平坦,但流动阻力却很大。 【三】流动中的动量传递 从传递的角度来分析牛顿粘性定律。假设所研究的流体为不可压缩流体,密度为常 数,则牛顿粘性定律可写成如下形式: -2-y (1-55) 式中:【一剪应力或动量通量,其单位为: -[]-[]-[] Y=片一运动粘度或称动量扩散系数,其单位为: 1-份=[怒]-m (p)一动量浓度,其单位为 【w=[g][]-[m] d(pw)/dy一动量浓度梯度,其单位为: []-[] 式(155)表示剪应力为单位时间通过单位面积的动量即动量通量是动量传递速率,它与 动量浓度梯度成正比,比例系数为动量扩散系数,负号表示动量传递的方向与动量浓度梯度的 方向相反,即动量由高速层向低速层传递。它类似于热能由高温处向低温处传递,物质由高浓