
1.3流体在管内流动的基本方程 19 Ra:+竖+A2=w,-∑h, (1-31) 或 g胶1+++w。=g2+2++∑h (1-32) 若流体为理想流体,∑h(=0,又无外功加入,W。=0,则 g1++=g2++ (1-33) 0 式(1-33)称为柏努利方程,式(1-31)和(132)是柏努利方程的引申,习惯上也称柏努利方 程式。 (三)柏努利方程的讨论 (1)柏努利方程式(1-33)适用于不可压缩理想流体作定态流动无外功输入的情况。该方 程表明1kg流体在流动沿程任一截面上具有的位能、动能和静压能之和为一常数。位能、动 能和静压能均为机械能,在流动过程中总机械能守恒,但各种形式的机械能可互相转换。 (2)由式(131)可知,当不可压缩实际流体在水平直管中定态流动时,若无外功加入,受 连续性方程的约束流速不变,克服阻力损失了机械能,致使流体的压强能降低,沿程压强减小。 (3)当流体静止时,=0,∑h:=0,W。=0,式(1-32)变成式(1-8) g1+色=g+ 该式即流体静力学方程,可见它是柏努利方程的特例。位能和压强能均为势能,式(1-8)表明 在同一静止流体中,不同位置的流体微元其位能和压强能各不相同,但两者之和即总势能各处 相同 (4)式(131)中,W。和∑:是流动过程中获得的能量和损失的能量。W。是输送机械对单 位质量流体做的有效功。单位时间做的有效功称为有效功率,以八。表示,单位为小s1或W。 Ne=W.qm (1-34) (5)衡算基准不同的柏努利方程式 不难看出,经过简单的公式变换,便可导出以下衡算基准不同,能量单位不同的柏努利方程 口以单位质量流体为基准的方程(1-32a)为 g1+g+色+w,=g+2+2+公 [J·kg] ☑以单位体积流体为基准的方程(1-32b)为 Pg1+g+p1+pm,=g1+y+2+P∑ [J·m3=Pa] ③以单位重量流体为基准的方程(1-32c)为 [J.N-I=m] 式1,32冲各项:爱是分别称为位压头、动压头,静压头,雨H,和分别称为有效压头 和压头损失。 针对不同情况采用不同形式的柏努利方程进行计算,比较方便。 (6)柏努利方程适用于不可压缩流体,液体压缩性很小,可近似看做不可压缩流体。气体
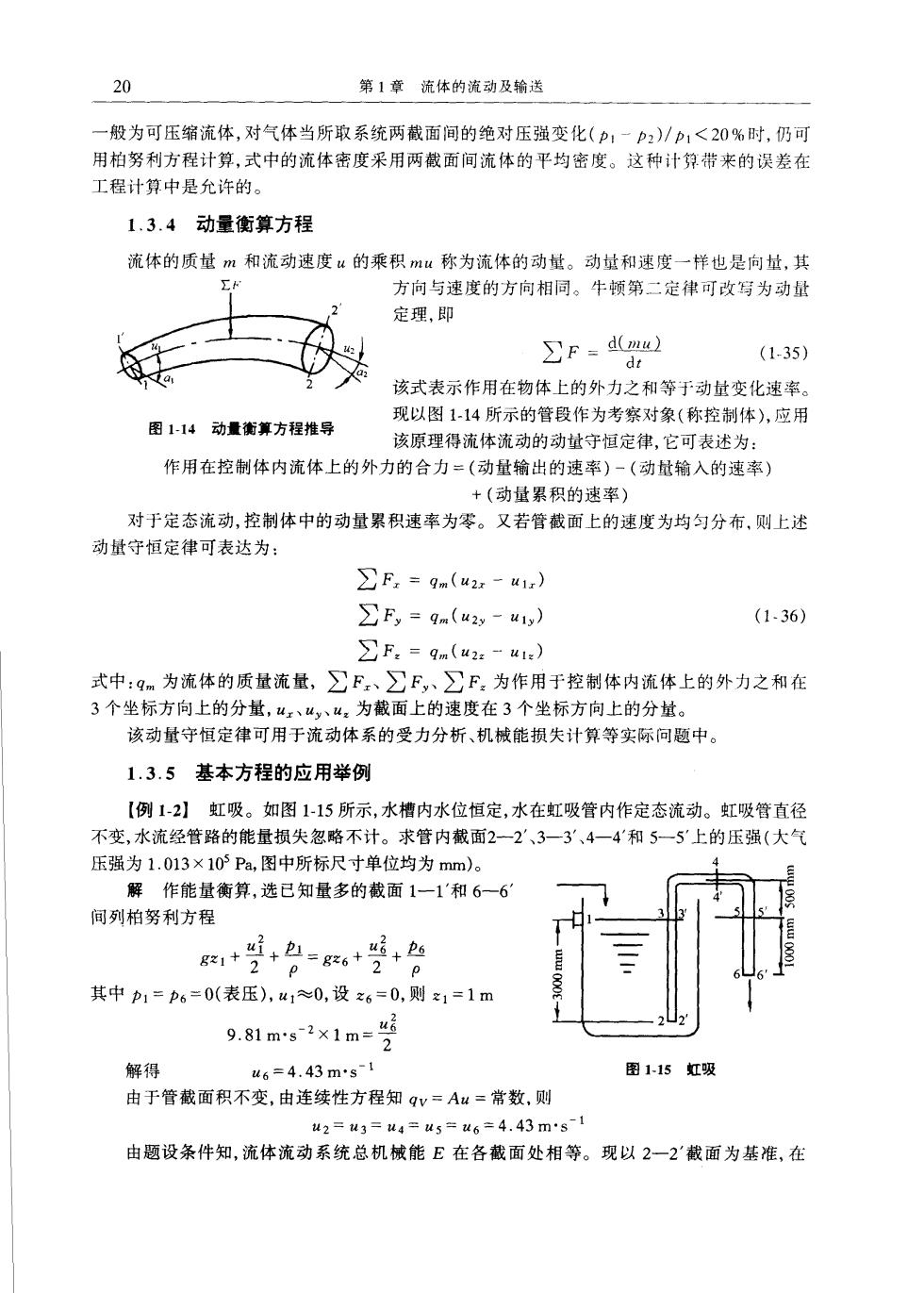
20 第1章流体的流动及输送 一般为可压缩流体,对气体当所取系统两截面间的绝对压强变化(1一2)/p1<20%时,仍可 用柏努利方程计算,式中的流体密度采用两截面间流体的平均密度。这种计算带来的误差在 工程计算中是允许的。 1.3.4动量衡算方程 流体的质址m和流动速度u的乘积mu称为流体的动量。动址和速度一样也是向址,其 方向与速度的方向相同。牛领第二定律可改写为动量 定理,即 ∑F=d(mw) dr (1.35) 该式表示作用在物体上的外力之和等于动量变化速率 图1-14动量衡算方程推导 现以图114所示的管段作为考察对象(称控制体),应用 该原理得流体流动的动量守恒定律,它可表沭为】 作用在控制体内流体上的外力的合力=(动量输出的速率)一(动量输入的速率) +(动量累积的速率) 对于定态流动,控制体中的动量累积速率为零。又若管截面上的速度为均匀分布,则上述 动量守恒定律可表达为: ∑F2=qm(42z-u1z) ∑Fy=9am(u2y-u1,) (1-36) ∑F2=qm(42:-u1:) 式中:qm为流体的质量流量,F、∑F,、∑F。为作用于控制体内流体上的外力之和在 3个坐标方向上的分量,、“,、“,为截面上的速度在3个坐标方向上的分址。 该动量守恒定律可用于流动体系的受力分析、机械能损失计算等实际问题中。 1.3.5基本方程的应用举例 【例12】虹吸。如图115所示,水槽内水位恒定,水在虹吸管内作定态流动。虹吸管直径 不变,水流经管路的能量损失忽略不计。求管内截面2一2'、3一3、4一4和5一5上的压强(大气 压强为1.013×10Pa,图中所标尺寸单位均为mm)。 解作能量衡算,选已知量多的截面1一1'和6一6 间列柏努利方程 g1++色=g6++ 其中p1=p6=0(表压),u1≈0,设x6=0,则1=1m 981ms2×1m= 解得 u6=4.43ms 图1-15虹吸 由于管截面积不变,由连续性方程知qv=Au=常数,则 2=w3=4=45=6=4.43m*81 由题设条件知,流体流动系统总机械能E在各截面处相等。现以2一2截面为基准,在

1.3流体在管内流动的基本方程 1一1和2一2截面间进行能量衡算,得 E=9.81mg2×3m+1,013X10里=130.8J+kg1 1000kgm- 从而得各截面处的压强 a-(E-gl0 =130.8J-kg1_4432s2-9.81ms2×0m×100kgm =1.21×105P8 p1=E-9-gp=9.16×10p p4=E-g4p=867x10Pa ps=E-号-gp=9.16x10Pa 由该例可见流体流动中的各机械能间的转换情况,等高处位能相同,1一1'处的静压能转 化为3一3'处的动能,即“3>41,则p3<p1。虹吸管内流速相同,动能处处相等,位置高位能 高,静压能必低,所以p4<p3<p2,p:<<p6 【例1-3】流向判断。如图1-16所示,在文丘里管的喉颈 处接一支管与下部水槽相通,文氏管的直管处的内径为 50mm,喉管处内径为15mm。当水以7m3.h-1的流量流过文 氏管时,截面1一1'处的表压强为0,02MPa。试判断垂直支管 中水的流向。假设流动无阻力,水的密度为1000kgm3。 解假设支管上有一阀门处于关闭状态。首先分析文丘 里管内流体流动,在截面1一1和2一2间列柏努利方程 图116流向判断 7m3h-1 其中 3600g.h-1 u10.785d0.785x0.05m=0.99ms1 p1=p,+0.02×106Pa=1.013×10Pa+0.02×106Pa=1.213×105Pa 由连续性方程得 =°=0.9m。1×03}=1.0mg 则 p2=1-号(u3-u)=6.09×104Pa 其次,再分析比较垂直支管上端面2处和支管下方3一3截面的势能。对于不可压缩流 体,位能和压强能均属势能。取水槽液面3一3为势能基准面,则支管上端面2和3一3截面的 势能之和分别为 6.09×104

第1章流体的流动及输送 1.013x103=101.3Jkg' 色3+&3g=100kgm 由于3一3处的势能大于2处的势能,若打开阀门时,流体则由下方向上流动。 【例14】流体流动阻力分析和实验测定。假设流体在管内作定态流动,且任一截面上 流体的流速、密度和压强均匀分布,如图117所示。根据 连续性方程,在管截面1一1和2一2间则有 01u1A1=02u2A3 对于该控制体内流动的流体,所受外力包括压力和 管壁摩擦阻力(忽略质量力),即 图117 流体流过导管的阻力分析 压力△p=p:A1-p2A2 阻力F:=rdA, (1-37) 式中:A,、A2一截面1一1'和2一2的横截面积:x一管壁剪应力即单位管壁面积施于流体的 阻力;A。一管壁面积 由动址衡算方程知 ∑F=qm(u2-u1) (1-38) ∑F=△p-F:=qn(u2-41) 则 F1=△p-qm(42-u1) (1-39) 式(1-39)即为计算流体流动阻力的基本方程。 对于均一直径为d、长为!的水平圆管内流动的不可压缩流体,有 tW1=42 F:=△p 即 rmdl=于d2(p1-pz) (1-40) 流体因克服阻力消耗能量,使静压能降低,压强减小,由此而降低的压强称为压强降,以 △p:表示,由式(140)得 △p:=p1-p2=4rl/d (1-41) 将上式进行变换 p=4x品×台×学-恶台受 pu (1-42 则 4p=A受 (1-43) 式中:无量纲系数λ称为摩掾系数。式(1-43)即计算圆型直管阻力的通式,称为范宁(Fanning)公

1.4流体的流动现象 23 式。 通过实验,测定在一定管径管长的直管内流体的平均流速和两端的压强,则可求得不同流 速下的λ值。 【例15】管道突然扩大。如图1-18所示,流体流过突然扩大管道时必伴有机械能损失。据柏 努利方程及连续性方程,有 M- ++-++ (a) 0 puA1=pu2A2 (b) 显然,由于h未知,即使1、1、d1、d2均已知,仍无法计 算出p2 再试用动址定理,为简化起见,设管道水平放置,即z1 图1-18突然扩大 z2。在截面1一1'和2一2'间流体所受外力示于图中,设管壁对流体的惨擦阻力F,与其他各 力相比可以忽略,则定态流动时,动量定理为 PIAI-P2A2+Fn=pAzu3-pAui (c) 式中:p1、p2分别为截面1一1'和2一2处的平均压强:F。一器壁对流体的作用力。 设截面1一1'处壁面对流体的压强近似等于p1,则 F。=p1(A2-A1) (d) 综合以上四式,联立求解,得 =1- (1-44) 这就方便地由突然变化的管截面积和变化前(即小管)的流速求得流体流经管道突然扩大处的能 量损失计算式。这里要注意,该式是联立了能量衡算式、质世衡算式和动量衡算式推导而得。 从以上的应用举例可以看出,流体流动同样遵守质量守恒定律、能量守恒定律和动址守 定律。每个规律都把相应的变量定量地关联起来,再将几个关系式联立求解,使实际问题得以 解决。另一方面也应注意到,在推导中作过简化假设,所以计算结果还应经实验去检验校正 在实际应用中,柏努利方程应用最广。在选取衡算截面时,应是不可压缩流体连续充满其 间作定态流动。所选的上下游截面要垂直于流动方向在平稳流动处,要便于进行有关物理址 的求算。物理量要取截面上的平均值。 1.4流体的流动现象 化工中的许多过程都与流体的流动现象的状态、结构有关,例如实际流体流动时的阻力、 流体的热量传递和流体的质量传递均与流动结构直接相关。流体流动结构问题很复杂,本节 只作简单讨论。 1.4.1牛顿粘性定理与流体的粘度 如前所述,流体具有易流动性,同时又具有抵抗两层流体相对滑动速度的性质即粘性。 (一】牛顿粘性定理 流体流动时存在内摩擦力,流体流动时必须克服内摩擦力做功。内摩擦力是一种平行于 流动方向的流体微元表面的表面力,常称做剪力。表面力与表面积成正比,单位面积上所受的